1049. 最后一块石头的重量

第一想法

/**
 * @param {number[]} stones
 * @return {number}
 */
var lastStoneWeightII = function (nums) {

    // 和分割两个和相等的子数组一样
    //dp[j]表示 背包总容量（所能装的总重量）是j，放进物品后，背的最大重量为dp[j]。
    //value[i]和weight[i] 数值
    // 结果，用来sum-dp[j]*2的最小值
    let sum = nums.reduce((x, y) => x + y)
    let dp = new Array(sum).fill(0);
    // 开始 01背包
    for (let i = 0; i < nums.length; i++) {
        for (let j = sum; j >= nums[i]; j--) { // 每一个元素一定是不可重复放入，所以从大到小遍历
            dp[j] = dp[j] > dp[j - nums[i]] + nums[i] ? dp[j] : dp[j - nums[i]] + nums[i]
        }
    }
    let i = 0
    let a = 100000000
    while (i < dp.length) {
        a = Math.abs(sum - dp[i] * 2) > a ? a : Math.abs(sum - dp[i] * 2)
        i++
    }
    return a
};

优化

不用算到最后面，就写到一般就好了

但js 中 n/a不会取整
用Math.floor(sum / 2);

/**
 * @param {number[]} stones
 * @return {number}
 */
var lastStoneWeightII = function(nums) {

 let sum=nums.reduce((x,y)=>x+y)
  let dpLen = Math.floor(sum / 2);
     let dp = new Array(dpLen+1).fill(0);
for(let i = 0; i < nums.length; i++) {
    for(let j = dpLen; j >= nums[i]; j--) { // 每一个元素一定是不可重复放入，所以从大到小遍历
        dp[j] = dp[j]> dp[j - nums[i]] + nums[i]? dp[j]:dp[j - nums[i]] + nums[i]
    }
}
return sum-dp[dpLen]*2
};

494. 目标和

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
var findTargetSumWays = function(nums, target) {
  let sum=nums.reduce((x,y)=>x+y)
  if((sum+target)%2) return 0
  if(Math.abs(target)>sum) return 0
  const hf=(sum+target)/2
  let dp = new Array(hf+1).fill(0);
  dp[0]=1
  for (let i = 0; i < nums.length; i++) {
        for (let j =hf; j >= nums[i]; j--) { // 每一个元素一定是不可重复放入，所以从大到小遍历
         dp[j] += dp[j - nums[i]]
        }
    }
    return dp[hf]
};

第一想法

排列组合

困难

• 问题转换

假设加法的总和为x，那么减法对应的总和就是sum - x。
所以我们要求的是 x - (sum - x) = target
x = (target + sum) / 2
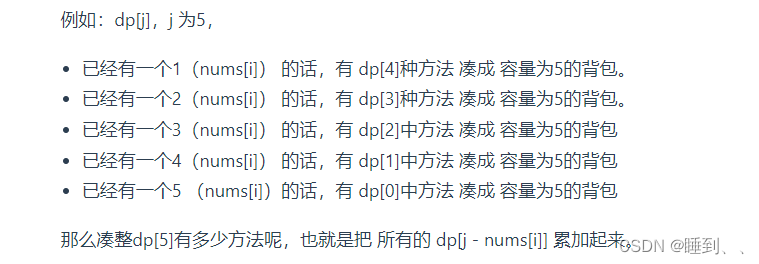
此时问题就转化为，装满容量为x的背包，有几种方法。

• dp[j] += dp[j - nums[i]]
  

总结

• dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
  一个限重的包装石头，石头有重量，有价值，怎样装最值钱
• dp[j] += dp[j - nums[i]]
  dp[j] 表示：填满j（包括j）这么大容积的包，有dp[j]种方法
  
  

一和零

const findMaxForm = (strs, m, n) => {
    const dp = Array.from(Array(m+1), () => Array(n+1).fill(0));
    let numOfZeros, numOfOnes;

    for(let str of strs) {
        numOfZeros = 0;
        numOfOnes = 0;
    
        for(let c of str) {
            if (c === '0') {
                numOfZeros++;
            } else {
                numOfOnes++;
            }
        }

        for(let i = m; i >= numOfZeros; i--) {
            for(let j = n; j >= numOfOnes; j--) {
                dp[i][j] = Math.max(dp[i][j], dp[i - numOfZeros][j - numOfOnes] + 1);
            }
        }
    }

    return dp[m][n];
};

思路

1. dp[i][j]：最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。

2. dp[i][j] 可以由前一个strs里的字符串推导出来，strs里的字符串有zeroNum个0，oneNum个1。
   dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。
   然后我们在遍历的过程中，取dp[i][j]的最大值。
   所以递推公式：dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
   此时大家可以回想一下01背包的递推公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
   对比一下就会发现，字符串的zeroNum和oneNum相当于物品的重量（weight[i]），字符串本身的个数相当于物品的价值（value[i]）。

这就是一个典型的01背包！ 只不过物品的重量有了两个维度而已。