[算法应用]关键路径算法的简单应用

news2024/11/20 3:33:49

(0)免责声明:

算法和数据结构都是我自己写的,为了提交这次的作业,所以把去年写过的算法重新翻新了一下,数据结构也简单整理了一下,重新放上来了.

整个程序是可以顺利跑通的,同学们可以用代码检测一下自己的结果对不对,切勿抄袭.

(真的不想手推关键路径了....真的....不过复习整个算法,还有重新编写数据结构确实花了点时间)

(1)问题描述

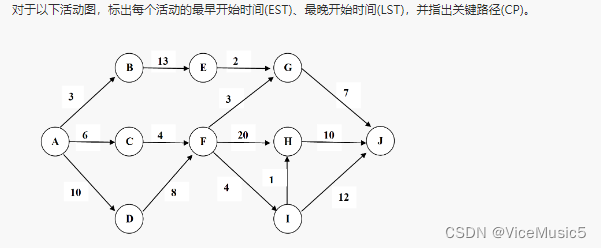
很简单,就是要est和lst,还有关键路径

(在下面的代码中,我们习惯性地称呼为etv和ltv)

数据分析,一共14条边,10个点,按照顺序从0开始算起,按照起点,终点,权重三要素,可以把数据划分为

(2)代码原理分析/算法逻辑

代码的实现逻辑是这样的

1.首先按照拓扑结构进行的,按照拓扑顺序遍历每个点,如点A,到下流点B这一路径上,如果B的最早开始时间早于A的最早时间加上A-B需要的时间,那么就把B的最早开始时间延后.

2.然后按照逆拓扑结构进行,如果A的最晚开始时间+A->B需要的时间晚于B的最晚开始时间,那么就把A的最晚开始时间往前移动

3.关键路径就是,A的最早开始时间+AB需要的时间=B的最晚开始时间,那么这条就是关键路径之一

(3)数据存储结构的实现

//图结构已经储存完毕;(graph为邻接表进行存储)
class Node {
public:
    int num;
    int weight;     //路径的消耗时间保存在终点上,视为路径徐娅萍的时间
    Node* next;
    Node(int a) { num = a; };
};
class headNode {
public:
    int length = 0;
    Node* point=NULL;
    int in, out = 0;
};
class graph {
public:
    headNode arr[20];
    int NodeNum, EdgeNum = 0;
};
void createGraph(graph& Graph) {
    int edge, point,start,end,weight;
    cout << "请输入边数 和 点数" << endl;
    cin >> edge >> point;
    Graph.EdgeNum = edge;
    Graph.NodeNum = point;
    for (int i = 0; i < point; i++) {
        Graph.arr[i] = headNode();
    }
    cout << "请按照顺序输入起点,终点,权重" << endl;
    for (int i = 1; i <= edge; i++) {
        cin >> start >> end >> weight;
        Graph.arr[start].out++;//出度+1
        Graph.arr[end].in++;//入度+1
        Node* temp = new Node(end);
        temp->weight = weight;//赋予权重
        temp->next = Graph.arr[start].point;
        Graph.arr[start].point = temp;//头插法插入
    }
}
//图结构已经储存完毕;

(4)完整代码

//关键路径算法
//受到学妹的启发,终于明白这个最短是什么意思了
//最短并非指的是从起点到终点的最短距离(事实上这个也能求,不过理论上不行)
//关键路径的时间加起来,其实是完成所有任务需要的最短时间(默认任务是可以并发完成的)
//感谢来自隔壁实验室的22级同学的讨论和提示
int etv[20];//最早开始时间
int ltv[20];//最晚开始时间
int top = 0;//指针
int Stack[20];//这是储存用到的栈,或者说是数组

//关键路径算法的实现
void topuGraph(graph& Graph) {
    stack<int> stack2;
    for (int i = 0; i < Graph.NodeNum; i++) {
        if (Graph.arr[i].in == 0)stack2.push(i);  //先把入度为0的点压入栈中
        etv[i] = 0;                               //设置每个点的最早开始时间为0
    }
    while (!stack2.empty()) {
        int temp = stack2.top();                  //获取一个出发点,并且弹出来,然后按照拓扑排序,保存一个信息
        stack2.pop();
        Stack[top++] = temp;
        Node* point = Graph.arr[temp].point;      //然后开始对点的所有下游点进行遍历
        while (point) {
            if (--Graph.arr[point->num].in == 0) { //先处理这个点作为入度的情况,也就是对下面的下游点们剔除这个点的影响
                stack2.push(point->num);
            }
            if (etv[point->num]<etv[temp]+point->weight) {//修改最早数值    : 如果这个点的最早开始时间,早于上一个任务的开始时间+完成需要时间
                etv[point->num] = etv[temp] + point->weight;   //就适当延后这个点的开始时间
            }
            point = point->next;
        }
    }
}


void keyRoad(graph& Graph) {
    for (int i = 0; i < Graph.NodeNum; i++) {
        ltv[i] = etv[Graph.NodeNum-1];              //给每个点都设置一个最晚的.或者足够大的最晚开始时间
    }
    while (top >= 0) {                              //拓扑排序从后往前(按照之前的顺序)
        int temp = Stack[top--];
        Node* point = Graph.arr[temp].point;       //同样是遍历这个点所有的子点
        while (point) {                            //如果最晚开始时间晚于子点的最晚开始时间-子点需要完成的时间,那么就把最晚开始时间往前调
            if (ltv[temp] > ltv[point->num] - point->weight) {
                ltv[temp] = ltv[point->num] - point->weight;
            }
            point = point->next;
        }
    }
    //在邻接表中寻找关键路径,
    //如果一个点的最早开始时间+这个点需要的时间恰好为下一个点开始的最早时间,那么这个路径就一定是关键路径了
    int ete, lte = 0;
    for (int i = 0; i < Graph.NodeNum; i++) {
        Node* point = Graph.arr[i].point;
        while (point) {
            ete = etv[i];
            lte = ltv[point->num]-point->weight;
            if (ete == lte) {
                cout<<"关键路径为"<<endl;
                cout << (char)(i+65) << "--->" << (char)(point->num+65) <<"("<<point->weight<<")" << endl;
            }
            point = point->next;
        }
    }
}


int main(){
    graph g;
    createGraph(g);
    topuGraph(g);
    keyRoad(g);
    cout<<"每个点的最早,最晚开始时间分别为:"<<endl;
    for (int i = 0; i < g.NodeNum; ++i) {
        cout<<(char)(i+65)<<"  最早开始时间为:"<<etv[i]<<", 最晚开始时间为:"<<ltv[i]<<endl;
    }
}

(5)跑通的最后结果

关键路径为
A--->D(10)
关键路径为
D--->F(8)
关键路径为
F--->H(20)
关键路径为
H--->J(10)
每个点的最早,最晚开始时间分别为:
A 最早开始时间为:0, 最晚开始时间为:0
B 最早开始时间为:3, 最晚开始时间为:26
C 最早开始时间为:6, 最晚开始时间为:14
D 最早开始时间为:10, 最晚开始时间为:10
E 最早开始时间为:16, 最晚开始时间为:39
F 最早开始时间为:18, 最晚开始时间为:18
G 最早开始时间为:21, 最晚开始时间为:41
H 最早开始时间为:38, 最晚开始时间为:38
I 最早开始时间为:22, 最晚开始时间为:36
J 最早开始时间为:48, 最晚开始时间为:48