目录
一. 堆排序
基本思想
代码实现
向上调整算法
向下调整算法
时间和空间复杂度
稳定性
二. 归并排序
基本思想
代码实现
时间和空间复杂度
稳定性
一. 堆排序
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似 完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于) 它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序
注意:排升序要建大堆,排降序建小堆
大顶堆:每个节点的值都大于或等于其子节点的值;
小顶堆:每个节点的值都小于或等于其子节点的值;
提示:此次以排升序建大堆为例
基本思想
将待排序的序列构造成一个大根堆。此时,整个序列的最大值就是堆顶的根结点。将它 移走(就是将其与堆数组的末尾元素交换,此时末尾元素就是最大值),然后把剩余的n-1个 序列重新构造成一个堆,就会得到n个元素中的次大值。如此反复执行,便能得到一个有序列。
算法步骤:
① 创建一个堆 Heap[0……n-1];
② 把堆首(最大值)和堆尾互换;
③ 把堆的尺寸缩小 1,并调用 shift_down(0),目的是把新的数组顶端数据调整到相应置;
④ 重复步骤 2,直到堆的尺寸为 1。
图示:

代码实现
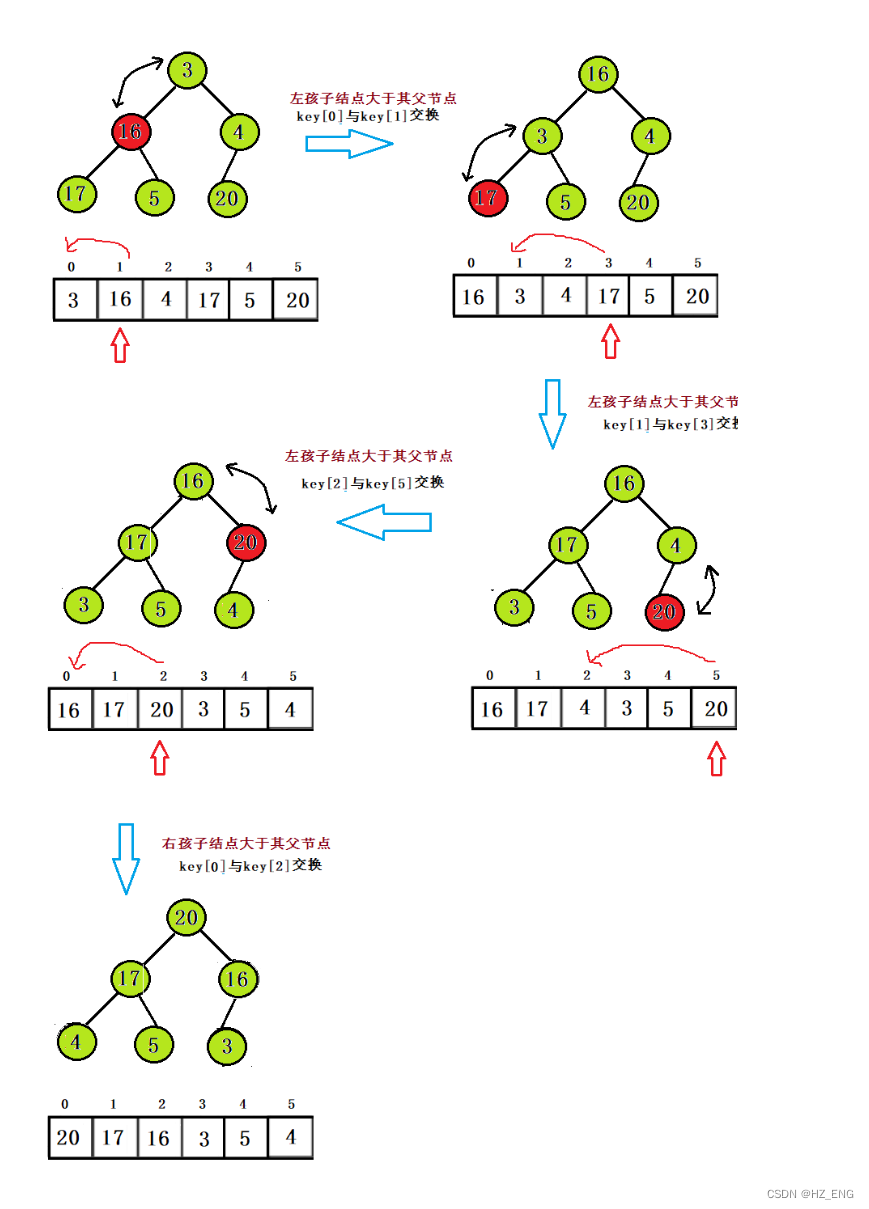
向上调整算法
思想方法:从第一个结点开始(视为左孩子或右孩子),先找该结点的父结点,在与父节点比较,大的与父结点交换,成为新的父节点;这样依次往下,直到最后一个节点。
知道孩子结点找父节点:左孩子、 右孩子:parent = (child - 1) / 2
图解:
void AdjustUp(int* a, int child)
{
int parent = (child - 1) / 2; //找父节点
while (child > 0)
{
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]); //与父结点交换
child = parent; //往后走到下一个结点
parent = (parent - 1) / 2;
}
else
break;
}
}
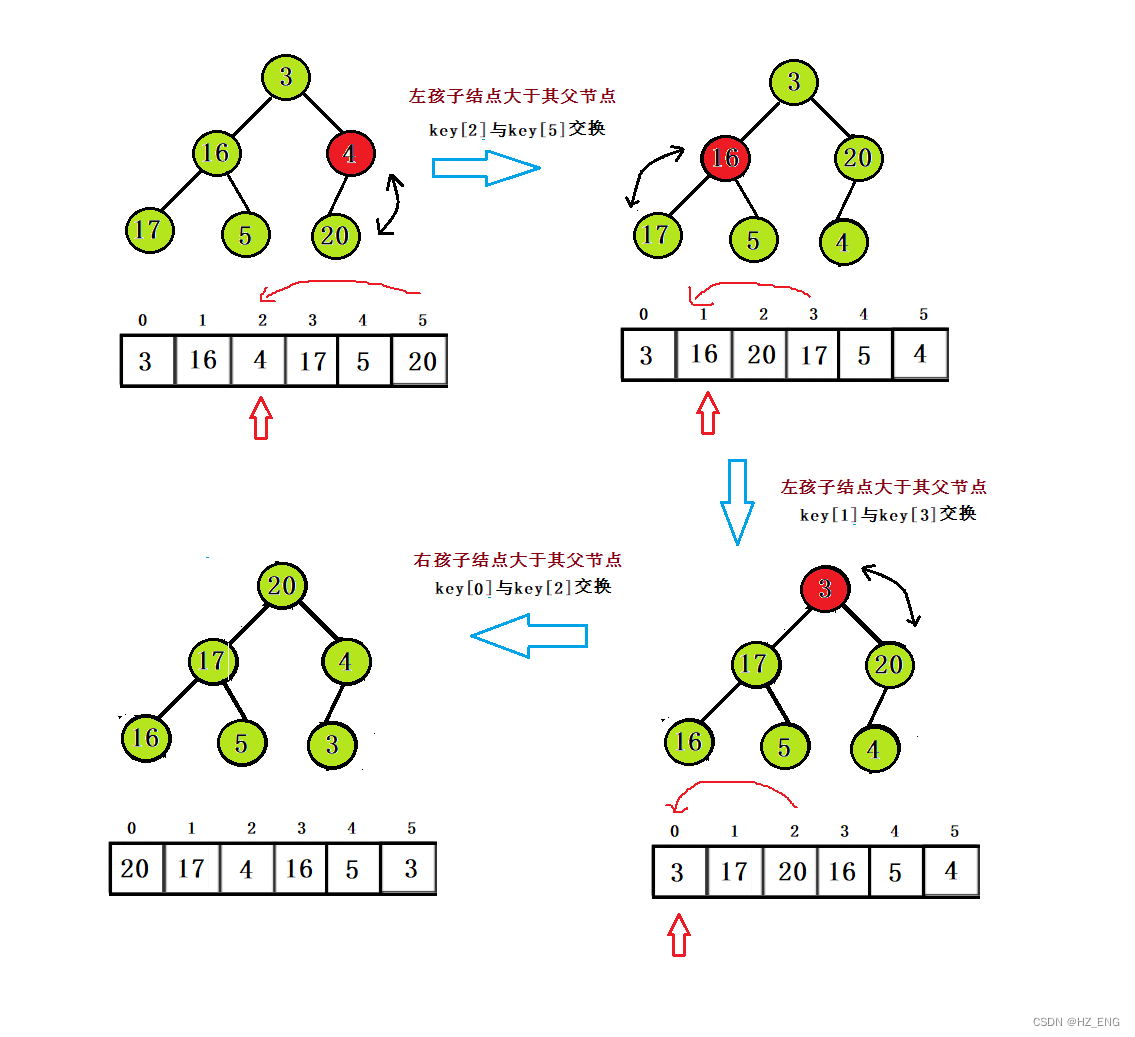
向下调整算法
思想方法:从最后一个元素开始(视为父节点),先找其孩子节点(左孩子或右孩子),与其孩 子结点比较,与大的一方(左孩子或右孩子)交换;依次往上,直到第一个结点。
知道父节点找孩子:child = parent * 2 + 1
图解:
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1; //找孩子
while (child < n)
{
//找左右孩子较小的
if (child+1 < n && a[child + 1] > a[child])
child++;
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]); //与父节点交换
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
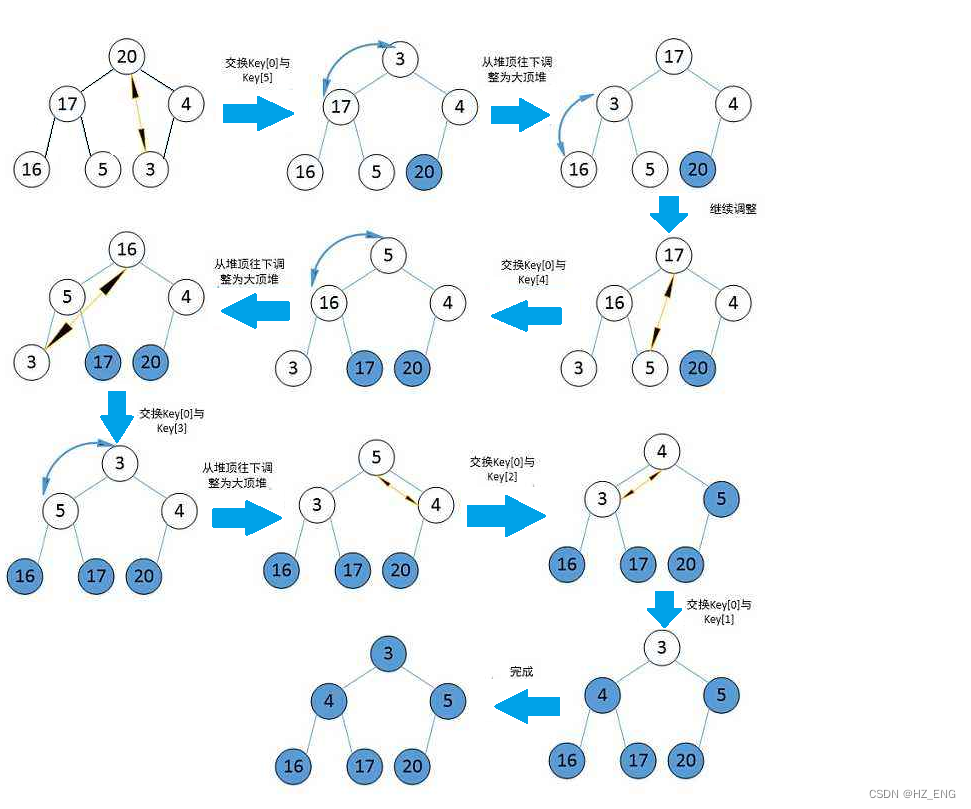
通过向上调整或向下调整算法建堆后,进行堆排序,此程序为向下调整建堆。
图解:
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
if (child+1 < n && a[child + 1] > a[child])
child++;
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
//堆排序
void HeapSort(int* a, int n)
{
//向下调整建堆
for (int i = (n-1-1)/2; i >= 0; i--)
{
AdjustDown(a,n,i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
end--;
}
}
时间和空间复杂度
时间复杂度:O(nlogn)
空间复杂度:O(1)
稳定性
堆排序:不稳定排序
二. 归并排序
基本思想
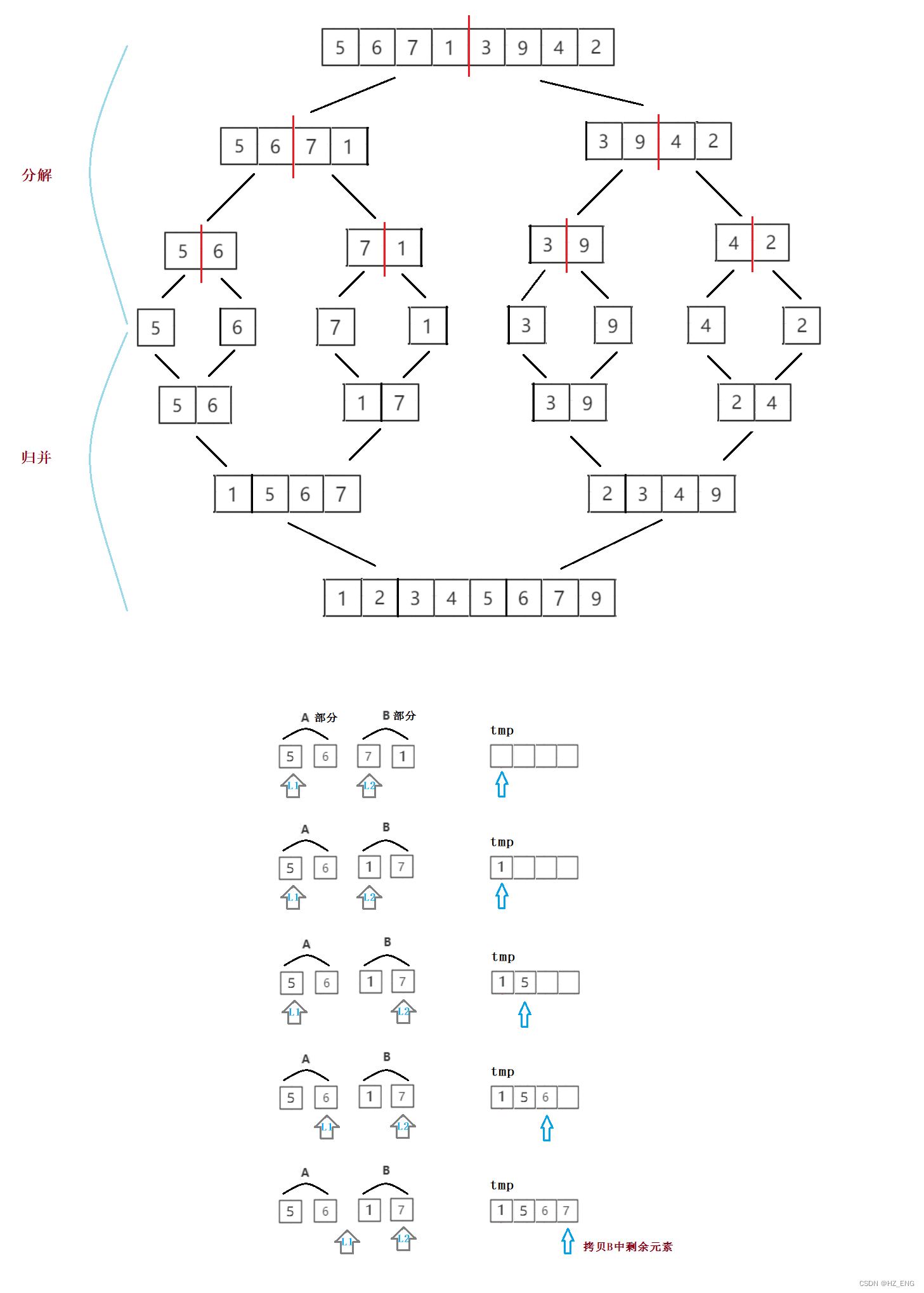
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段 间有序。若将两个有序表合并成一个有序表,称为二路归并
算法步骤:
① 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
② 设定两个指针,最初位置分别为两个已经排序序列的起始位置;
③ 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
④ 重复步骤 3 直到某一指针达到序列尾;
⑤ 将另一序列剩下的所有元素直接复制到合并序列尾;
图示
代码实现
void _MergeSort(int* a, int* tmp, int left, int right)
{
if (left >= right)
return;
int mid = (left + right) / 2;
_MergeSort(a, tmp, left, mid); //递归左边
_MergeSort(a, tmp, mid+1, right); //递归右边
// 将a数组元素归并到tmp数组,再拷贝回a数组
int left1 = left, right1 = mid;
int left2 = mid + 1, right2 = right;
int index = left;
while (left1 <= right1 && left2 <= right2)
{
if (a[left1] <= a[left2])
tmp[index++] = a[left1++];
else
tmp[index++] = a[left2++];
}
while(left1 <= right1) //左>右,将左区间剩余元素拷贝到tmp数组
tmp[index++] = a[left1++];
while(left2 <= right2) //左<右,将右区间剩余元素拷贝到tmp数组
tmp[index++] = a[left2++];
//拷贝回原数组
memcpy(a + left, tmp + left, sizeof(int) * (right - left + 1));
}
//归并排序
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
_MergeSort(a, tmp, 0, n - 1);
free(tmp);
}
时间和空间复杂度
时间复杂度:O(nlogn)
空间复杂度:O(n) 归并排序时需要和待排序记录个数相等的存储空间
稳定性
归并排序:稳定排序