系列文章目录

第一章 Python 机器学习入门之线性回归
第一章 Python 机器学习入门之梯度下降法

前言

上一篇文章里面说到了用梯度下降法来对最小化代价函数和模型参数进行求解，那究竟是为什么呢？

一、梯度下降法

1.梯度下降法简介

梯度下降百科的定义：
梯度下降法（Gradient descent）是一个一阶最优化算法，是迭代法的一种，用于求解最小二乘问题

这上面的说法更像是阐述了梯度下降法的性质和作用，博主偏私人的理解是该算法是指在求解最小化代价函数和模型参数的过程中沿着梯度下降的方向来一步步迭代求解的算法，听起来好像还是有点问题，什么是梯度？

梯度百科定义：梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）

这个其实比较好理解了，我们高中时就学过导数这一概念，导数是判断函数变化程度的函数，往往用在寻找函数的极大值和极小值上，这通常用于二维平面上；而梯度就是寻找函数变化程度最大的某个方向，属于三维立体方向。
那梯度下降法就是在此基础上寻找函数的局部最小值或全局最小值，由此也可以推导出梯度上升法，是在此基础上寻找函数的局部最大值或全局最大值，这里就不过多阐述了。

2.基本原理

从最简单的线性回归模型来说，它的模型函数为

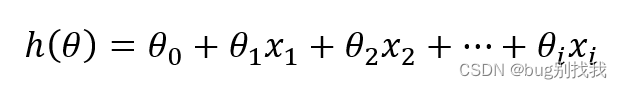
损失函数如下，h(x)为模型预测值，y为实际值，计算二者误差平方用来判断损失

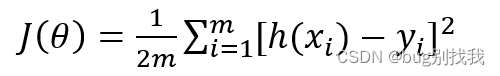
而梯度下降函数形式为，意为接下来的模型参数θ_(n+1)等于当前的模型参数θ_(n)减去学习率a乘以损失函数对当前模型参数求偏导

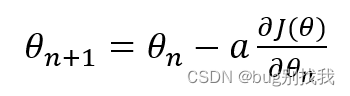
到这一步是不是有点懵，接下来我们就来推导一下；首先我们使用泰勒近似定理的一阶展开式子（下面的倒三角标识梯度）

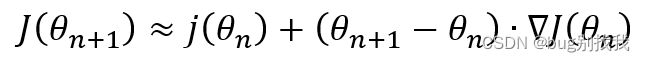
因为我们的目的是让损失函数最小化，易知

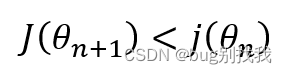
因此推导出

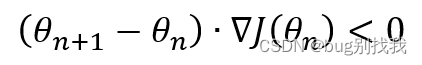
而我们希望上面这个式子越小越好，这样我们每次迭代的变化量就会很大，更快地找到最小化损失函数；我们注意到θ_(n+1)和∇J(θ)均为向量，根据向量相乘定理，当向量夹角为180度时，二者最小，因此推导出

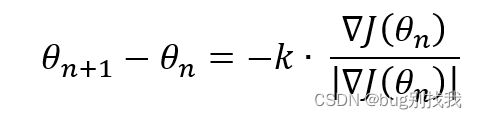
上式意为沿着∇J(θ）相反方向的一个向量，k代表变化程度，属于一个未知变量，k右边的式子代表单位向量，因此将它们化简得出

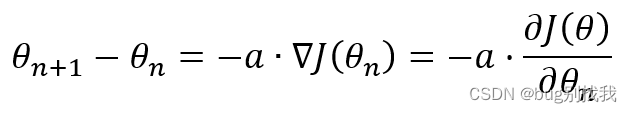
梯度下降函数效果展示