一、线性回归的原理

1、线性回归应用场景
如何判定一个问题是回归问题的，目标值是连续型的数据的时候

房价预测
销售额度预测
贷款额度预测、利用线性回归以及系数分析因子

2、线性回归定义
线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式

找到一种函数关系，来表示特征值和目标值之间的关系

3、函数关系

（1）首先假定特征值x1、x2、x3
（2）目标值是h(w)
（3）每个特征前还有个系数，w1、w2、w3，叫做权重值，也叫回归系数
（4）右边+b，叫做偏置系数
（5）只有一个自变量的情况称为单变量回归，大于一个自变量情况的叫做多元回归

用习惯的写法：
y = w1x1 + w2x2 + w3x3 + ... + wnxn + b
  = wTx + b

PS：wT叫做w的转置

例子：
期末成绩：0.7×考试成绩 + 0.3×平时成绩
预测房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率

4、广义线性模型
线性回归当中的关系有两种，一种是线性关系，另一种是非线性关系。在这里我们只能画一个平面更好去理解，所以都用单个特征举例子

（1）线性关系

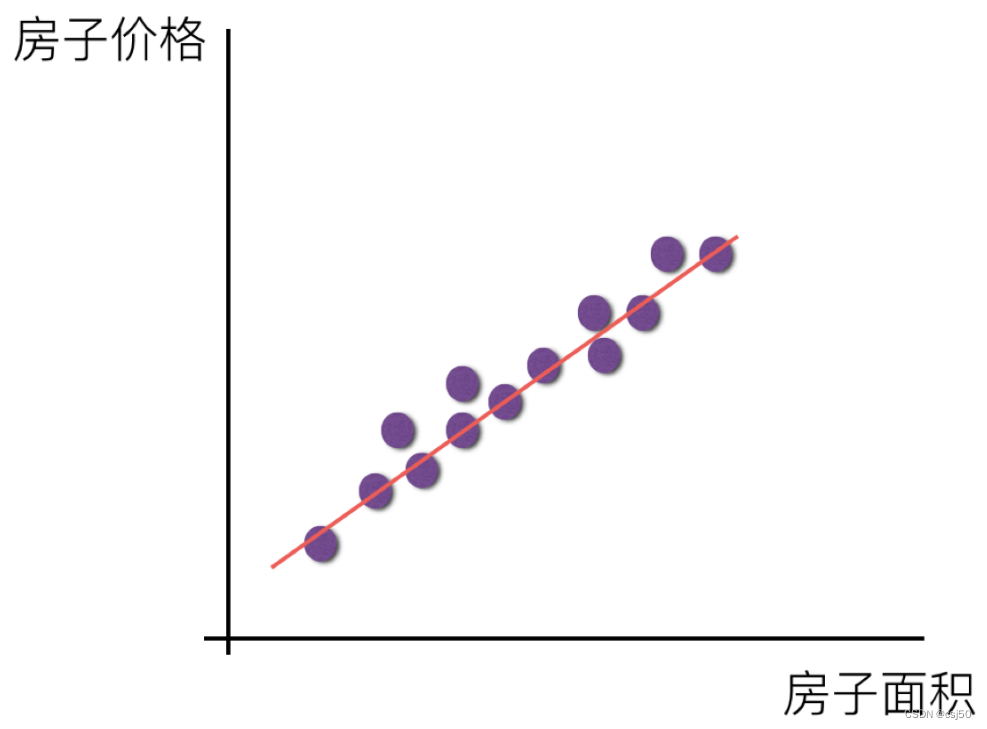
特征只有一个房屋面积，预测房屋价格，在一个平面当中，可以找到一条直线去拟合他们之间的关系，y = kx + b

如果有两个特征：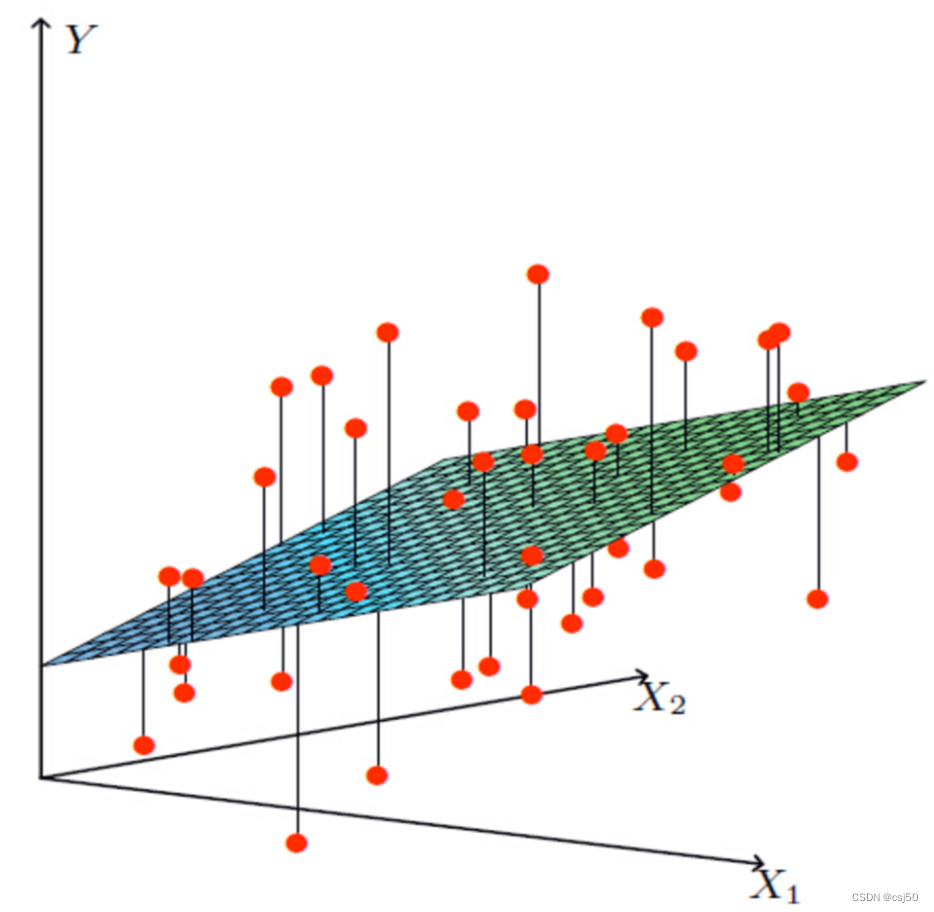

要拟合x1、x2和y之间的关系，y = w1x1 + w2x2 + b

如果在单特征与目标值的关系呈直线关系，或者两个特征与目标值呈现平面的关系
更高维度的我们不用自己去想，记住这种关系即可

（2）非线性关系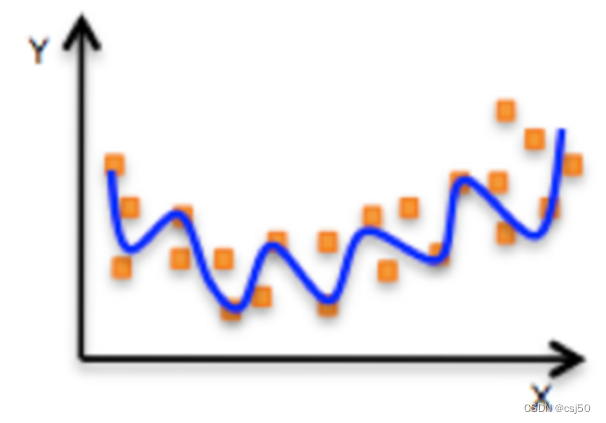

为什么非线性关系，也叫线性模型
线性模型
  自变量一次
  y = w1x1 + w2x2 + w3x3 + ... + wnxn + b
  参数一次
  y = w1x1 + w2x1^2 + w3x1^3 + w4x2^3 + ... + b
  就是w和x有一个是一次的，不是多次的，都可以叫线性模型
  
（3）线性关系&线性模型
线性关系一定是线性模型，线性模型不一定是线性关系