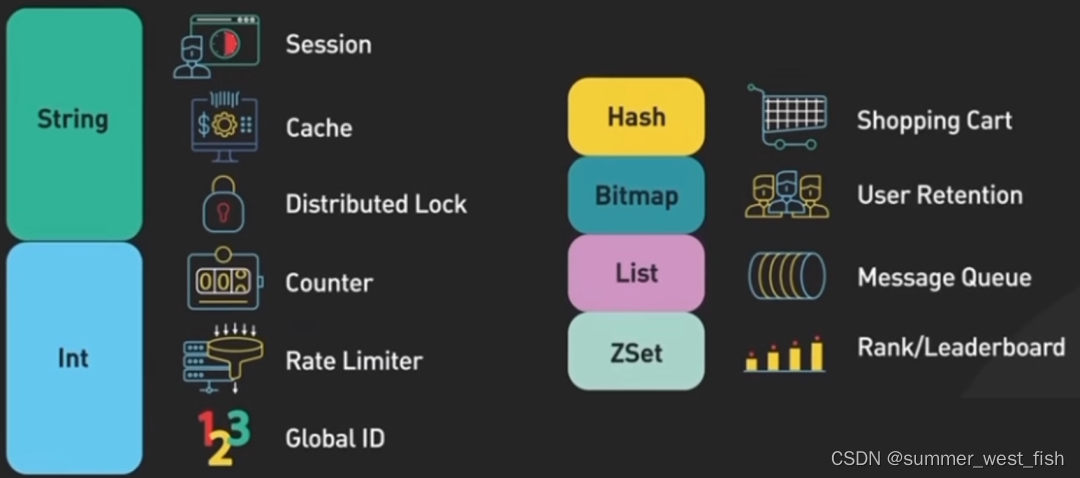
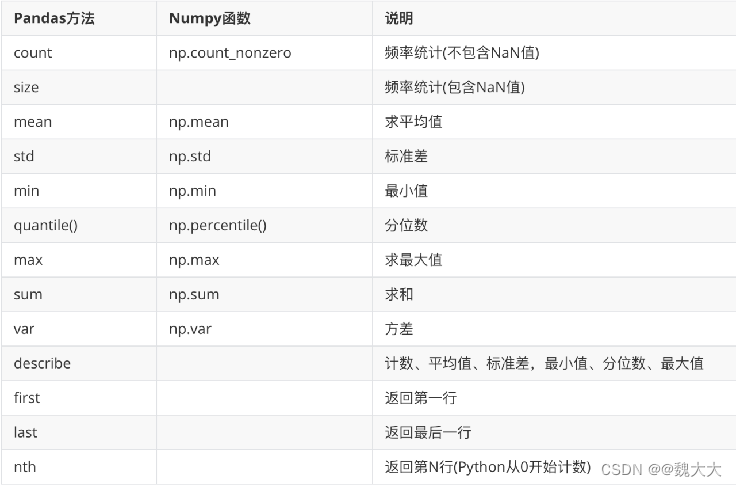
数据结构与算法
- 算法基础
- 时间复杂度
- 空间复杂度
- 递归
- 实例:汉诺塔问题
- 查找
- 顺序查找(线性查找)
- 二分查找(折半查找)
- 比较
- 排序
- 冒泡排序
- 选择排序
- 插入排序
- 快速排序
- 快排和冒泡的时间比较
- 堆排序
- 树
- 堆
- 堆的向下调整
- 堆排序过程
- 时间复杂度
- 堆的内置模块
- 堆排序→topk问题
- **有n个数,得到前k大的数。(k<n)**
- 归并排序
- NB总结
- 希尔排序
- 计数排序
- 题目:已知整数的范围是0~100,设计时间复杂度O(n)的算法
- 桶排序 (不是特别重要)
- 基数排序
- 查找排序部分习题
- 数据结构
- 列表/数组
- 栈 stack 后进先出LIFO(last-in, first out)
- 括号匹配问题
- 队列 queue 先进先出FIFO(first-in, first out)
- 队列用列表实现:环形队列
- 内置模块 双向队列
- 打印文件后五行
- 迷宫问题(栈 队列)
- 栈:深度优先搜索dfs 回溯法
- 队列:广度优先搜索bfs
- 链表
- 创建链表
- 链表节点的插入 删除(注意顺序)
- 双链表 插入 删除
- 复杂度分析
- 哈希表
- 直接寻址表
- 哈希
- 解决哈希冲突:开放寻址法
- 拉链法
- 应用:集合与字典
- md5算法
- SHA-2算法
- 树
- 二叉树 Binary Tree
- 遍历
- 前序遍历 根 左子树 右子树
- 中序遍历 左子树 根 右子树
- 后序遍历 左子树 右子树 根
- 层次遍历 需要用到队列
- 给两个遍历 求树
- 二叉搜索树
- 二叉搜索树 插入
- 二叉搜索树 查询
- 二叉搜索树 删除
- AVL树 至少要懂原理
- AVL扩展:b树
- 算法进阶
- 贪心:当前最好的选择。局部最优解。
- 背包问题 (01背包 分数背包)
- 拼接最大数字问题(面试经常出)
- 活动选择问题(也很经典)
- 动态规划 dynamic programming
- 钢条切割问题
- 最长公共子序列
- 欧几里得算法
- RSA加密算法(主流加密)
算法基础
Algorithm
程序=数据结构+算法
时间复杂度
时间复杂度:估计算法运行时间的一个式子(单位)
for i in range(n) n是问题的规模
while n>1:
print(n)
n=n//2
n=64 2的6次方=64 每次运算,运算量都会缩小一半,折半情况都会出现logn.
复杂度O(logn)或O(log2n)
一般来说,复杂度高的慢。与机器有关系,与n有关系。
判断算法复杂度:(简单算法)
- 确定规模n
- 循环减半过程→logn
- k层关于n的循环→nk
空间复杂度
空间复杂度:评估算法内存占用大小
使用几个变量O(1)
使用长度为n的一维列表:O(n)
使用m行n列的二维列表:O(mn)
“空间换时间” 减少时间
递归
特点:调用自身,结束条件。
实例:汉诺塔问题
n个圆盘3个柱子abc 一次动一个盘子
代码

查找
内置列表查找函数:index() 是线性查找
顺序查找(线性查找)
时间复杂度O(n)
def linear_search(li, val):
for ind, v in enumerate(li):
if v == val:
return ind
else:
return None
二分查找(折半查找)
搜索候选区减少一半
两个变量 0 n-1 双指针
时间复杂度O(logn)
使用前先排序
def binary_search(li, val):
left = 0
right = len(li) - 1
while left <= right: # 候选区有值
mid = (left + right) // 2
if li[mid] == val:
return mid
elif li[mid] > val: # 待查找的值在mid左侧
right = mid - 1
else: # li[mid] < val 待查找的值在mid右侧
left = mid + 1
else:
return None
比较
from cal_time import *
@cal_time
def linear_search(li, val):
for ind, v in enumerate(li):
if v == val:
return ind
else:
return None
@cal_time
def binary_search(li, val):
left = 0
right = len(li) - 1
while left <= right: # 候选区有值
mid = (left + right) // 2
if li[mid] == val:
return mid
elif li[mid] > val: # 待查找的值在mid左侧
right = mid - 1
else: # li[mid] < val 待查找的值在mid右侧
left = mid + 1
else:
return None
# li = [1,2,3,4,5,6,7,8,9]
# print(binary_search(li, 3)) # 2
li = list(range(100000000))
linear_search(li, 38900000)
binary_search(li, 38900000)
# linear_search running time: 6.46293044090271 secs.
# binary_search running time: 0.0 secs.
排序
升序与降序
内置排序函数:sort()
常见排序算法
- 冒泡 选择 插入(复杂度都是O(n2),都是原地排序);
- 快速 堆 归并;
- 希尔 计数 桶 基数
冒泡排序
时间复杂度O(n2)/最好O(n)
默认升序排列: 相邻数前面比后面大→交换,遍历一次,有序区+1,无序区-1。(最大数上去)
共走了n-1趟
关键点 趟,无序区范围。
n长度,第i趟,无序区还有n-i个数,箭头最后指到n-i-1
def bubble_sort(li):
for i in range(len(li) - 1): # 第i趟
for j in range(len(li) - i - 1):
if li[j] > li[j+1]: # 前>后 交换 → 从小到大
li[j], li[j+1] = li[j+1], li[j]
冒泡排序优化:其中一趟没交换,说明已经有序,可以直接结束算法。“if not exchange return”
def bubble_sort(li):
for i in range(len(li) - 1): # 第i趟
exchange = False
for j in range(len(li) - i - 1):
if li[j] > li[j+1]: # 前>后 交换 → 从小到大
li[j], li[j+1] = li[j+1], li[j]
exchange = True
print(li)
if not exchange:
return
# li = [9,8,7,1,2,3,4,5,6] # 后几趟都没交换,可优化算法
# # li = [random.randint(0, 10000) for i in range(1000)]
# print(li)
# bubble_sort(li)
# # print(li)
# [8, 7, 1, 2, 3, 4, 5, 6, 9]
# [7, 1, 2, 3, 4, 5, 6, 8, 9]
# [1, 2, 3, 4, 5, 6, 7, 8, 9]
# [1, 2, 3, 4, 5, 6, 7, 8, 9]
选择排序
时间复杂度O(n2)
(simple方法)每次找最小的数 拿出来。缺点:多占一个内存。
min、append、remove, min和remove都占复杂度。
def select_sort_simple(li): # 多占一个内存
li_new = []
for i in range(len(li)): # i 是第几趟
min_val = min(li)
li_new.append(min_val)
li.remove(min_val)
return li_new
无序区找数,数和第一个数交换。
关键点 有序区和无序区,无序区最小数位置
def select_sort(li): # 无序区找数 数和第一个数交换
for i in range(len(li) - 1): # 最后剩的数一定是最大值
min_loc = i # 找到最小值下标
for j in range(i + 1, len(li)):
if li[j] < li[min_loc]:
min_loc = j
li[i], li[min_loc] = li[min_loc], li[i]
插入排序
时间复杂度O(n2)
初始(有序区)一张牌,每次从无序区摸一张牌,插到已有牌的正确位置
def insert_sort(li):
for i in range(1, len(li)): # i 表示摸到的牌下标 无序区
tmp = li[i] # 往后挪防止覆盖掉无序区第一张牌
j = i - 1 # j 是手里的牌下标 有序区
while j >= 0 and li[j] > tmp: # 大的牌往后挪 最多到 j=-1 前停止 → 摸到的牌最小
li[j + 1] = li[j]
j -= 1
li[j + 1] = tmp # 放到不挪的牌的后边
print(li)
快速排序
时间复杂度O(nlogn) /最坏情况O(n2)
- 取一个元素p,归位
- 列表分成两部分,<p & p & >p
- 递归(两边都要递归)
(第一轮:第一个元素p取出→左边有空位,从右边开始找比p小的数填空位→右边有空位,从左边找。直到left==right)
def partition(li, left, right): # p 归位,列表分两部分
tmp = li[left] # 取出第一个p
while left < right:
while left < right and li[right] >= tmp: # 找比p小的数(监视不让l和r碰上(循环里的循环会不受限制地一直减))
right -= 1 # right大就不动值,指针往左走
li[left] = li[right] # right 的数写到 left 上
# print(li)
while left < right and li[left] <= tmp: # 如果第一个while已经l=r了这个while就不执行
left += 1
li[right] = li[left] # left 的数写到 right 上
# print(li)
li[left] = tmp # tmp归位 循环完插入p该在的位置
return left
def quick_sort(li, left, right): # 快排
if left < right:
mid = partition(li, left, right)
quick_sort(li, left, mid - 1)
quick_sort(li, mid + 1, right)
li = [5,7,4,6,3,1,2,9,8]
print(li)
quick_sort(li, 0, len(li)-1)
print(li)
快排和冒泡的时间比较
from cal_time import *
import random
import copy
def partition(li, left, right): # p 归位,列表分两部分
tmp = li[left] # 取出第一个p
while left < right:
while left < right and li[right] >= tmp: # 找比p小的数(监视不让l和r碰上(循环里的循环会不受限制地一直减))
right -= 1 # right大就不动值,指针往左走
li[left] = li[right] # right 的数写到 left 上
# print(li)
while left < right and li[left] <= tmp: # 如果第一个while已经l=r了这个while就不执行
left += 1
li[right] = li[left] # left 的数写到 right 上
# print(li)
li[left] = tmp # tmp归位 循环完插入p该在的位置
return left
def _quick_sort(li, left, right): # 快排
if left < right:
mid = partition(li, left, right)
_quick_sort(li, left, mid - 1)
_quick_sort(li, mid + 1, right)
@cal_time
def quick_sort(li):
_quick_sort(li, 0, len(li) - 1)
# li = [5,7,4,6,3,1,2,9,8]
li = list(range(10000))
random.shuffle(li)
# li = list(range(100, 0, -1)) # 考虑最坏情况 倒序
li1 = copy.deepcopy(li)
li2 = copy.deepcopy(li)
# print(li)
quick_sort(li1)
from bubble_sort import *
bubble_sort(li2)
# print(li1)
# print(li2)
# quick_sort running time: 0.05300426483154297 secs.
# bubble_sort running time: 20.663341999053955 secs.
堆排序
(不用递归。)
时间复杂度O(nlogn) 实际比快速排序慢一点
树
树:一种可以递归定义的数据结构
度:分几个叉
二叉树:度<=2
二叉树存储方式:链式存储方式、顺序存储方式
父节点与左孩子节点下标:i → 2i+1 j → (j-1)//2
父节点与右孩子节点下标:i → 2i+2 j → (j-1)//2
堆
堆:一种特殊的完全二叉树(叶节点只出现在最下层和次下层 & 最下节点都集中在左侧若干位置)结构
大根堆 任一节点比孩子节点大 (堆排序是以大根堆为例)
小根堆 任一节点比孩子节点小
堆的向下调整
性质:左右子树都是堆但根不满足,依次向下调整
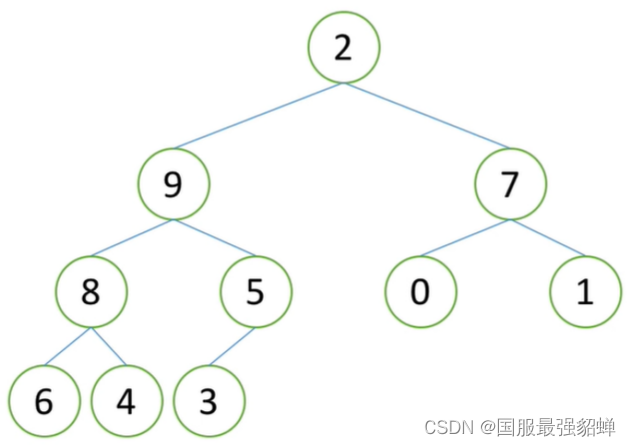
2拿出来,9和7中9大,9上去,8上去,6上去,2放到叶子结点。
堆排序过程
- 建立堆
- 得到堆顶元素为最大元素
- 去掉堆顶 堆最后一个元素放到堆顶 此时可通过一次向下调整重新使堆有序
- 堆顶元素为第二大元素
- 重复3直到堆变空
建立/构造堆:看最后一个非叶子节点(直到根节点),和叶子结点比较。
def sift(li, low, high):
"""
堆的向下调整
:param li: 列表
:param low: 堆的根节点位置
:param high: 堆的最后一个元素的位置
:return:
"""
i = low # i开始指向根节点
j = 2 * i + 1 # j开始指向左孩子
tmp = li[low] # 存堆顶
while j <= high: # 只要j位置有数
if j + 1 <= high and li[j + 1] > li[j]: # 如果右孩子大 j就指向右孩子
j = j + 1
if li[j] > tmp:
li[i] = li[j]
i = j # 往下看一层
j = 2 * i + 1
else: # tmp更大 把tmp放到i的位置上
li[i] = tmp
break
else:
li[i] = tmp # 下边没有叶子结点了,直接指向这个位置
def heap_sort(li):
n = len(li)
for i in range((n-2)//2, -1, -1): # 最后一个非叶子节点(直到根节点),和叶子结点比较
# i 为建堆的时候调整的部分根的下标
sift(li, i, n-1)
# 建堆完成 当前堆顶最大
for i in range(n - 1, -1, -1):
# i 指向当前堆的最后一个元素
li[0], li[i] = li[i], li[0]
sift(li, 0, i - 1) # i-1是新的high
li = [i for i in range(100)]
import random
random.shuffle(li)
print(li)
heap_sort(li)
print(li)
时间复杂度
建堆 sift:O(logn)
堆向下调整 heap_sort:两个O(nlogn)
堆排序:O(nlogn)
堆的内置模块
堆的内置模块 Python里有,可以直接调用 import heapq。q:queue,优先队列(队列 小的/大的先出)。
heapify建立一个小根堆;heapop弹出一个(最小)元素
import heapq # 实现的是小根堆 q → queue 优先队列
import random
li = list(range(100))
random.shuffle(li)
print(li) # [64, 87, 5, 55, 28, 30, ...]
heapq.heapify(li) # 建堆
print(li) # [0, 1, 2, 3, 11, 4, 5, ...]
n = len(li)
for i in range(n): # 弹出一个最小值
print(heapq.heappop(li), end=',') # 0,1,2,3,4,5,...
堆排序→topk问题
有n个数,得到前k大的数。(k<n)
解决思路:
| 步骤 | 复杂度 |
|---|---|
| 排序后切片 | O(nlogn) or O(nlogn+k) |
| 排序lowB 冒泡 选择 插入 | O(kn) |
| 堆排序 | O(nlogk) |
思路:
- 取列表前k元素建立一个小根堆,堆顶就是目前第k大的数(堆顶最小)
- 依次遍历原列表,小于堆顶则忽略,大于堆顶则更换该元素(堆顶)并调整堆
- 遍历所有元素,倒叙弹出。
# 比较排序
def sift(li, low, high): # @File : heap_sort.py
i = low # i开始指向根节点
j = 2 * i + 1 # j开始指向左孩子
tmp = li[low] # 存堆顶
while j <= high: # 只要j位置有数
if j + 1 <= high and li[j + 1] < li[j]: # 如果右孩子小 j就指向右孩子 # 改为小根堆
j = j + 1
if li[j] < tmp: # 改为小根堆
li[i] = li[j]
i = j # 往下看一层
j = 2 * i + 1
else: # tmp更大 把tmp放到i的位置上
li[i] = tmp
break
else:
li[i] = tmp # 下边没有叶子结点了,直接指向这个位置
def topk(li, k):
heap = li[0:k]
# 1. 建堆
for i in range((k-2)//2, -1, -1): # 建立一个小根堆,堆顶就是目前第k大的数
sift(heap, i, k - 1)
# 2. 遍历
for i in range(k, len(li) - 1): # 大于堆顶则更换该元素(堆顶)并调整堆
if li[i] > heap[0]:
heap[0] = li[i]
sift(heap, 0, k - 1)
# 3. 输出
for i in range(k - 1, -1, -1):
# i 指向当前堆的最后一个元素
heap[0], heap[i] = heap[i], heap[0]
sift(heap, 0, i - 1) # i-1是新的high
return heap
import random
li = list(range(100))
print(li)
random.shuffle(li)
print(li)
topk(li, 10)
print(topk(li, 10))
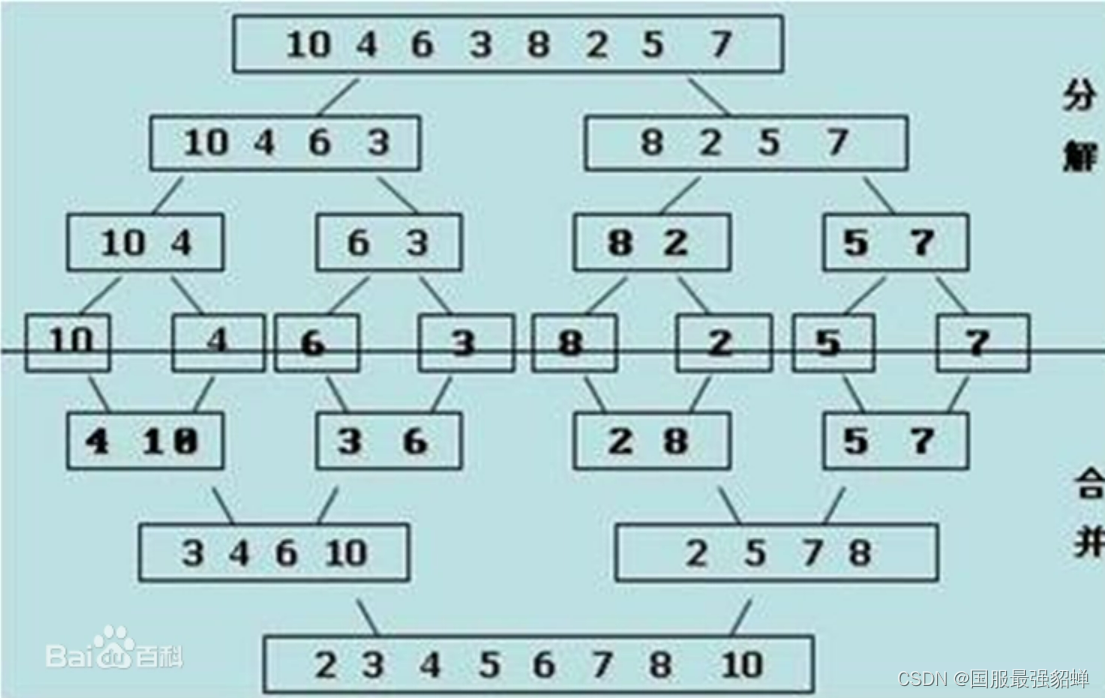
归并排序
一次归并merge:两个有序列表合并成一个。 low到mid一段,mid+1到high一段。移动i、j。时间O(n)。
归并 共logn层,时间复杂度O(nlogn)。
开了一个临时空间ltemp,空间复杂度O(n),之前的排序都是原地排序。
使用:
- 分解 列表(一分为二)越分越小,直到分成一个元素
- 终止条件 一个元素是有序的
- 合并 两个有序列表归并,列表越来越大
def merge(li, low, mid, high): # 一次归并 两段low~mid,mid+1~high
i = low
j = mid + 1
ltmp = []
while i <= mid and j <= high: # 只要左右两边都有数
if li[i] < li[j]:
ltmp.append(li[i])
i += 1
else:
ltmp.append(li[j])
j += 1
# while执行完,有一部分没数了
while i <= mid:
ltmp.append(li[i])
i += 1
while j <= high:
ltmp.append(li[j])
j += 1
li[low:high + 1] = ltmp
# li = [2,4,5,7,1,3,6,8]
# merge(li, 0, 3, 7)
# print(li)
def merge_sort(li, low, high):
if low < high: # 至少有2个元素 递归
mid = (low + high) // 2
merge_sort(li, low, mid)
merge_sort(li, mid + 1, high)
merge(li, low, mid, high)
li = list(range(8))
import random
random.shuffle(li)
print(li)
merge_sort(li, 0, len(li) - 1)
print(li)
NB总结
时间复杂度 O(nlogn)
运行时间:快速<归并<堆
缺点:
- 快速 极端情况下排序效率低,
- 归并 需要额外内存开销,
- 堆 快速排序算法中相对较慢

(递归函数里有空间消耗)
排序稳定性也比较重要 元素值一样时保证相对位置不变。
很多语言把sort定为归并。
希尔排序
分组插入排序算法。使整体数据越来越接近有序。

- 取第一个整数d1=n/2,将元素分为d1个组,每组相邻两元素之间距离为d1,组内插入排序
- 取整数d2=d1/2,重复,直到di=1(所有元素在同一组内直接插入排序)
时间复杂度比较复杂,和gap有关。上述最复杂的复杂度为O(n2)
维基百科:

def insert_sort_gap(li, gap): # gap分的组
for i in range(gap, len(li)): # i 表示摸到的牌下标 无序区
tmp = li[i] # 往后挪防止覆盖掉无序区第一张牌
j = i - gap # j 是手里的牌下标 有序区
while j >= 0 and li[j] > tmp: # 大的牌往后挪 最多到 j=-1 前停止 → 摸到的牌最小
li[j + gap] = li[j]
j -= gap
li[j + gap] = tmp # 放到不挪的牌的后边
# print(li)
def shell_sort(li):
d = len(li) // 2
while d >= 1:
insert_sort_gap(li, d)
d //= 2
li = list(range(10))
import random
random.shuffle(li)
print(li)
shell_sort(li)
print(li)
计数排序
题目:已知整数的范围是0~100,设计时间复杂度O(n)的算法
需要建一个新列表
复杂度O(n)
def count_sort(li, max_count=100):
count = [0 for _ in range(max_count + 1)] # 建一个新列表
for val in li:
count[val] += 1
li.clear() # 清空li把val打印count次
for ind, val in enumerate(count):
for i in range(val):
li.append(ind)
import random
li = [random.randint(0, 100) for _ in range(1000)]
print(li)
count_sort(li)
print(li)
桶排序 (不是特别重要)
元素范围较大,改造计数算法。
每个范围的元素放一个桶里,分别排序。

表现取决于数据的分布。
时间复杂度平均O(n+k),最坏O(n2k)。
空间复杂度O(nk) 占用了一个桶的空间
(k根据 n列表长度 m桶个数 =logmlogn)
def bucket_sort(li, n=100, max_num=10000):
buckets = [[] for _ in range(n)] # 创建桶 二维列表
for var in li:
# 一个桶放 (max_num // n) 个数 一个var放在 var // (max_num // n) 号桶
# var=10000时放到100号桶会越界 取一个min
i = min(var // (max_num // n), n - 1)
buckets[i].append(var) # 把var入桶
# 保持桶内顺序。 每插入一个数,其中的桶都排序 插入3 [0,2,4,3]
for j in range(len(buckets[i]) - 1, 0, -1): # 遍历一遍3的位置到2的位置
if buckets[i][j] < buckets[i][j - 1]:
buckets[i][j], buckets[i][j - 1] = buckets[i][j - 1], buckets[i][j] # [0,2,3,4]
else:
break
sort_li = []
for buc in buckets:
sort_li.extend(buc)
return sort_li
import random
li = [random.randint(0, 10000) for i in range(100)] # 100 个数
# print(li)
li = bucket_sort(li)
print(li)
基数排序
(多关键字排序)
先个位数(低位)排序 进桶,再高位排序 进桶
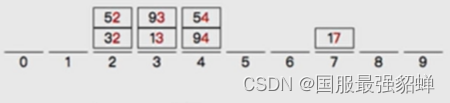
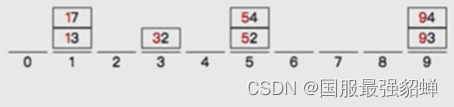
最大数的位数是几就是几次循环 k
时间复杂度O(kn) k是以10为底的对数 →O(nlog10k)。线性时间复杂度,比NB快。
(NB最快的)快排O(nlog2n)以2为底。
k过大时基排就慢了。
空间复杂度O(k+n)
def radix_sort(li):
max_num = max(li) # 最大值→it 99→2 888→3 10000→5
it = 0 # 迭代次数iter
while 10 ** it <= max_num: # 从个位开始,运行完一轮 it+1 到十位
buckets = [[] for _ in range(10)]
for var in li:
# 987 it=1取8 987//10=98 98%10=8 ; it=2取9 987//100=9 9%10=9
digit = (var // 10 ** it) % 10
buckets[digit].append(var)
# 分桶完成
li.clear()
for buc in buckets:
li.extend(buc)
# 把数重新写回li
it += 1
li = list(range(100))
import random
random.shuffle(li)
print(li)
radix_sort(li)
print(li)
查找排序部分习题
查找排序部分习题
242.有效的字母异位词
74.搜索二维矩阵
1.两数之和
167.两数之和 II
数据结构
- 线性结构 一对一
- 树结构 一对多
- 图结构 多对多
列表/数组
顺序存储元素
基本操作:按下标查找 插入元素 删除元素…
时间复杂度O(n)
32位机器上一个整数占4字节,一个地址也占4个字节
数组 列表不同:数组元素类型要相同,数组长度固定
栈 stack 后进先出LIFO(last-in, first out)
进栈/压栈 push li.append
出栈 pop li.pop
取栈顶 gettop li[-1]
class Stack:
def __init__(self):
self.stack = []
def push(self, element):
self.stack.append(element)
def pop(self):
return self.stack.pop()
def get_top(self):
if len(self.stack) > 0:
return self.stack[-1]
else:
return None
def is_empty(self):
return len(self.stack) == 0
# stack = Stack()
# stack.push(1)
# stack.push(2)
# stack.push(3)
# print(stack.pop()) # 3
# print(stack.pop()) # 2
# print(stack.pop()) # 1
括号匹配问题
一个字符串包括 {} [] () ,是否匹配
20. 有效的括号
class Stack:
def __init__(self):
self.stack = []
def push(self, element):
self.stack.append(element)
def pop(self):
return self.stack.pop()
def get_top(self):
if len(self.stack) > 0:
return self.stack[-1]
else:
return None
def is_empty(self):
return len(self.stack) == 0
def brace_match(s):
match = {'}': '{', ']': '[', ')': '('} # 字典
stack = Stack()
for ch in s: # 遍历字符串
if ch in {'(', '[', '{'}: # 左括号进栈
stack.push(ch)
else: # ch in {'}', ']', ')'} # 右括号进栈情况
if stack.is_empty(): # 栈空
return False
elif stack.get_top() == match[ch]: # 栈顶元素=字典对应的元素 pop栈顶元素
stack.pop()
else: # stack.get_top() != match[ch]
return False
if stack.is_empty(): # 遍历完s判断栈是否为空
return True
else:
return False
print(brace_match('[([{}])]()([{}])'))
print(brace_match('[{]'))
队列 queue 先进先出FIFO(first-in, first out)
插入:队尾rare,进队/入队
删除:队头front,出队
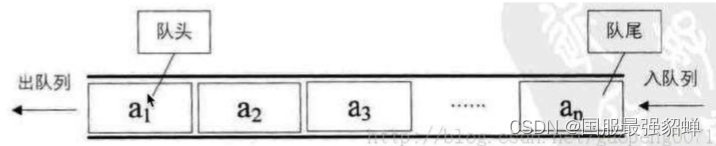
队列用列表实现:环形队列
循环队列最多元素个数是 MaxSize - 1 个
环形队列
队首/队尾指针 == maxsize - 1 时(maxsize是队列大小),再前进一个位置就自动到0
- 队首指针前进1:
front = (front + 1) % MaxSize - 队尾指针前进1:
rare = (rare + 1) % MaxSize
队空条件:rare == front
队满条件:(rare + 1) % MaxSize == front

class Queue:
def __init__(self, size=100):
self.queue = [0 for _ in range(size)] # 创建一个大小为size的列表
self.size = size
self.rear = 0 # 队尾 进队
self.front = 0 # 队首 出队
def push(self, element):
if not self.is_filled():
self.rear = (self.rear + 1) % self.size
self.queue[self.rear] = element
else:
raise IndexError("Queue is filled.")
def pop(self):
if not self.is_empty():
self.front = (self.front + 1) % self.size
return self.queue[self.front]
else:
raise IndexError("Queue is empty.")
# 判断队空
def is_empty(self):
return self.rear == self.front
# 判断队满
def is_filled(self):
return (self.rear + 1) % self.size == self.front
# q = Queue(5)
# for i in range(4): # 0 1 2 3 4
# q.push(i)
# print(q.is_filled()) # True
# print(q.pop()) # 0
# q.push(10) # 1 2 3 4 10
# print(q.pop()) # 1
# print(q.pop()) # 2
# print(q.pop()) # 3
# print(q.pop()) # 10
新建了一个queue.py debug 错误
AttributeError: 'Queue' object has no attribute 'put'
Can't process net command: 501 1 0.1 WIN
冲突了。改成 queue1.py
内置模块 双向队列
双向队列 dequeue 两端都支持进队出队
Python有队列内置模块。
from collections import deque
# from collections import deque
#
# # q = deque()
# q = deque([1, 2, 3, 4, 5], 5) # 已经满了,再append(6)之后2自动出队
# q.append(6) # 队尾进队
# print(q.popleft()) # 队首出队
#
# # 双向队列
# q.appendleft(1) # 队首进队
# q.pop() # 队尾出队
打印文件后五行
from collections import deque
def tail(n):
with open('test.txt', 'r') as f: # with open() as f的用法 r 只读
q = deque(f, n)
return q
print(tail(5)) # deque(['dghbtf\n', 'ert\n', 'ert\n', 'ertrty\n', 'fgn'], maxlen=5)
for line in tail(5):
print(line, end='')
# dghbtf
# ert
# ert
# ertrty
# fgn
迷宫问题(栈 队列)
490.迷宫
迷宫系列(0490, 0499, 0505)
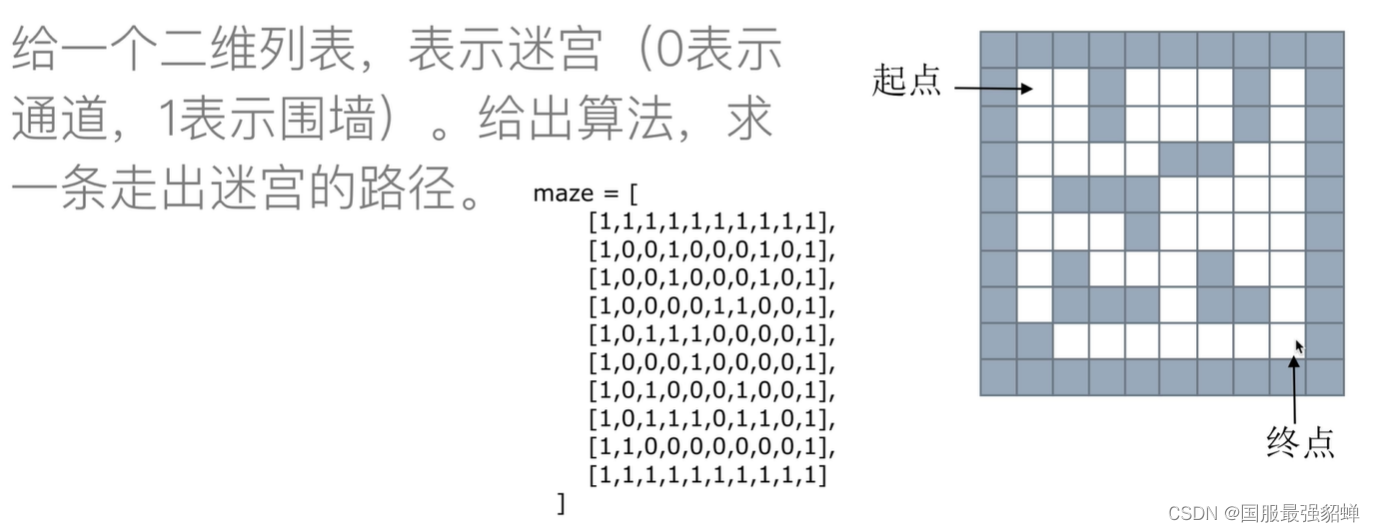
栈:深度优先搜索dfs 回溯法
栈里存路径→走过的路径太多(可能有死循环)
maze = [
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 0, 0, 1, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
[1, 0, 0, 0, 1, 0, 0, 0, 0, 1],
[1, 0, 1, 0, 0, 0, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 1, 1, 0, 1],
[1, 1, 0, 0, 0, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
]
dirs = [
lambda x, y: (x + 1, y), # 下
lambda x, y: (x - 1, y), # 上
lambda x, y: (x, y - 1), # 左
lambda x, y: (x, y + 1) # 右
]
def maze_path(x1, y1, x2, y2): # 输入起点终点位置
stack = [(x1, y1)] # 存储路径
nextNode = [0, 0]
while len(stack) > 0:
curNode = stack[-1] # 栈顶 当前节点 curNode[0] = x curNode[1] = y
if curNode[0] == x2 and curNode[1] == y2: # 当前走到终点
for p in stack:
print(p)
return True
for dir in dirs:
nextNode = dir(curNode[0], curNode[1])
# 如果下一个节点能走
if maze[nextNode[0]][nextNode[1]] == 0:
stack.append(nextNode)
maze[nextNode[0]][nextNode[1]] = 2 # 标记走过的位置
break # 找到一个能走的点
else: # 当前节点走不动
maze[nextNode[0]][nextNode[1]] = 2 # 标记走过的位置
stack.pop() # 回退一个位置
else:
print("没有路")
return False
maze_path(1, 1, 8, 8)
队列:广度优先搜索bfs
bfs 寻找所有接下来能继续走的点
队列存储当前正在考虑的节点
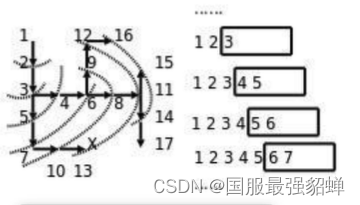
6 7 8 9 6出8 9进
7 8 9 10 7出10进
8 9 10 11 8出 11进
9 10 11 12 9出12进
10 11 12 13 10出13进
路径再从13倒退回1
需要新建一个额外的列表,记录这个点是那个点(几号位)出来的
| 0号位 | 1号位 | 2号位 | 3号位 | 4号位 | 5号位 | 6号位 |
|---|---|---|---|---|---|---|
| site1 | site 2 | site 3 | site 4 | site 5 | site 6 | site 7 |
| -1 | 0 | 1 | 2 | 2 | 3 | 4 |
如果6号位的site7是终点位:site 7→site 5→site 3→site 2→site 1
from collections import deque
maze = [
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 0, 0, 1, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
[1, 0, 0, 0, 1, 0, 0, 0, 0, 1],
[1, 0, 1, 0, 0, 0, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 1, 1, 0, 1],
[1, 1, 0, 0, 0, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
]
dirs = [
lambda x, y: (x + 1, y), # 下
lambda x, y: (x - 1, y), # 上
lambda x, y: (x, y - 1), # 左
lambda x, y: (x, y + 1) # 右
]
def print_r(path):
curNode = path[-1]
realpath = []
while curNode[2] != -1: # 路径退回起始点
realpath.append(curNode[0:2])
curNode = path[curNode[2]]
realpath.append(curNode[0:2]) # 放入起点
realpath.reverse()
for node in realpath:
print(node)
def maze_path_queue(x1, y1, x2, y2):
queue = deque()
queue.append((x1, y1, -1))
path = [] # 空列表 放入坐标
while len(queue) > 0:
curNode = queue.popleft() # 当前节点出队放入curNode
path.append(curNode) # 用path记录当前点坐标
if curNode[0] == x2 and curNode[1] == y2: # 终点
print_r(path)
return True
for dir in dirs:
nextNode = dir(curNode[0], curNode[1])
if maze[nextNode[0]][nextNode[1]] == 0:
queue.append((nextNode[0], nextNode[1], len(path) - 1)) # 后续节点进队queue,记录是从当前点的path来
maze[nextNode[0]][nextNode[1]] = 2 # 标记为已经走过
else:
return False
maze_path_queue(1, 1, 8, 8)
链表
一系列节点组成的元素集合
包含数据域item和指向下一个节点的指针next
class Node:
def __init__(self, item):
self.item = item
self.next = None
a = Node(1)
b = Node(2)
c = Node(3)
a.next = b
b.next = c
print(a.next.next.item) # 3
创建链表
头插法 尾插法

class Node:
def __init__(self, item):
self.item = item
self.next = None
def create_linklist_head(li):
head = Node(li[0])
for element in li[1:]: # 从1位开始
node = Node(element)
node.next = head
head = node
return head
def create_linklist_tail(li):
head = Node(li[0])
tail = head
for element in li[1:]:
node = Node(element)
tail.next = node
tail = node
return head
def print_linklist(li):
while li:
print(li.item, end='')
li = li.next
# lk = create_linklist_head([1, 2, 3])
lk = create_linklist_tail([1, 2, 3])
print(lk.item) # 3 1
print_linklist(lk) # 321 123
链表节点的插入 删除(注意顺序)
插入
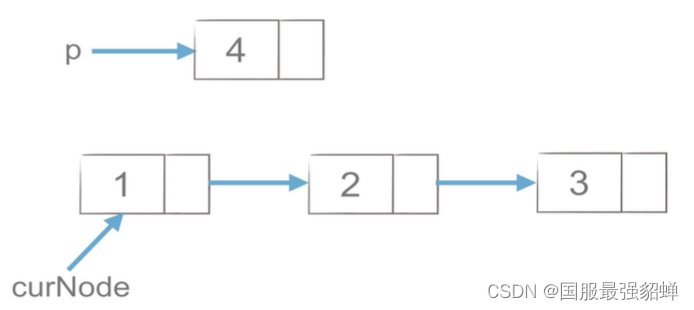
4连2 p.next=curNode.next
1连4 curNode.next=p
删除
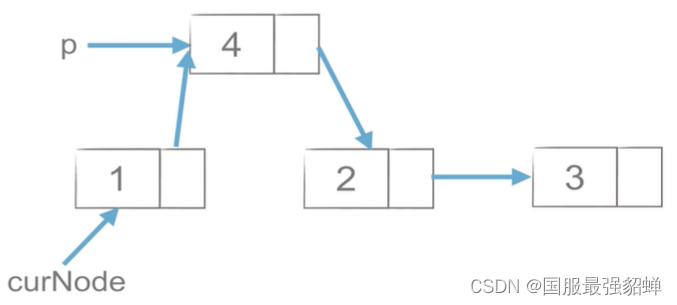
p连4 p=curNode.next
1连2 curNode.next=curNode.next.next
删除p del p
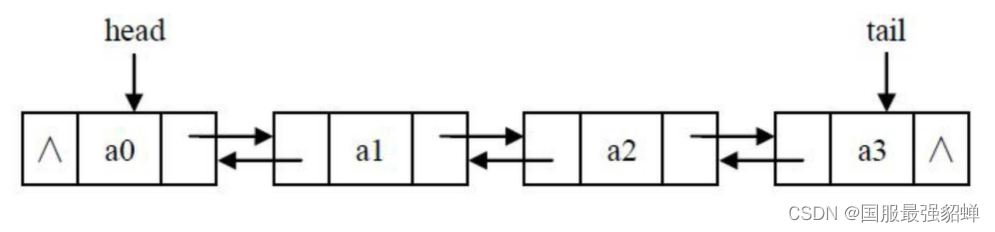
双链表 插入 删除
插入
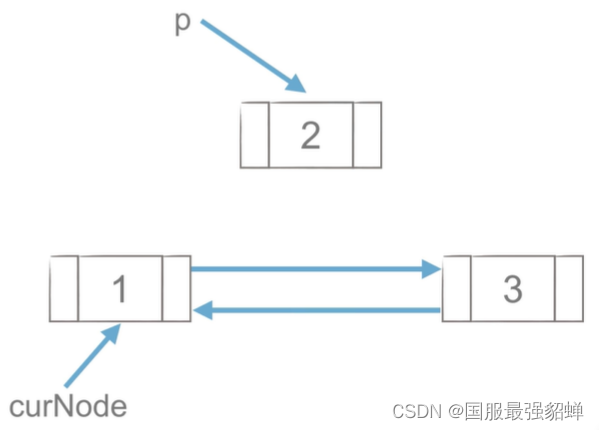
2→3 p.next=curNode.next
2←3 curNode.next.prior=p
1←2 p.prior=curNode
1→2 curNode.next=p
删除
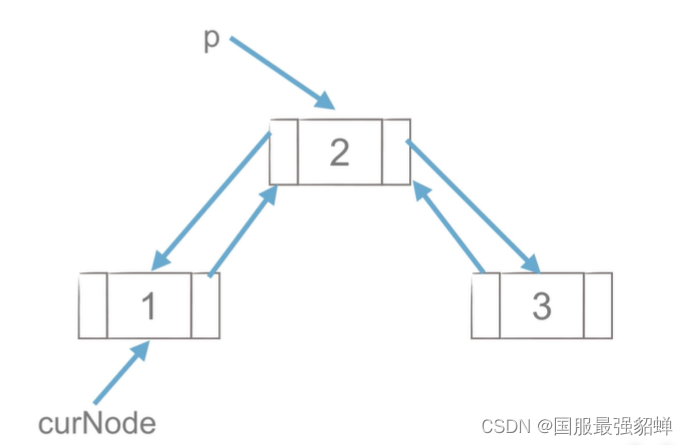
p连2 p=curNode.next
1→3 curNode.next=p.next
3←1 p.next.prior=curNode
删除p del p
复杂度分析
| 操作 | 顺序表(列表/数组) | 链表 |
|---|---|---|
| 按元素值查找 | O(n) | O(n) |
| 按下标查找 | O(1) | O(n) |
| 某元素后插入 | O(n) | O(1) |
| 删除某元素 | O(n) | O(1) |
链表的内存可以更灵活的分配
链表的这种链式存储的数据结构对树和图的结构有很大启发性
哈希表
(字典和集合会使用)
通过哈希函数来计算数据存储位置的数据结构
insert(key,value) 插入键值对(key,value)
get(key) 存在key返回其值value,否则返回空值
delete(key) 删除键为key的键值对
直接寻址表
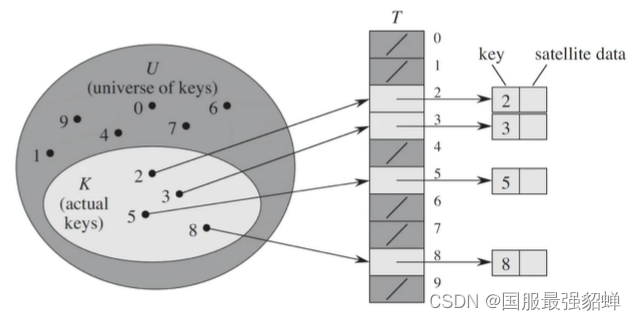
阈U小时使用。
缺点:
- 阈U很大时需要消耗大量内存,
- 阈U很大key很少时大量空间被浪费,
- 无法处理关键字不是数字的情况。
直接寻址表: key为k的元素放到k位置上。
改进直接寻址表:哈希
直接寻址表 + 哈希函数h(k) = 哈希表
哈希
哈希:
- 构建大小为m的寻址表T
- key为k的元素放到h(k)位置上
- h(k)是一个函数,将其阈U映射到表T[0,1,…,m-1]。

h(0)=h(7)=… 到了一个位置上,产生哈希冲突。
哈希冲突:两个不同元素映射到同一位置
解决哈希冲突:开放寻址法
开放寻址法:如果哈希函数返回的位置已经有值,则向后探查新的位置存储这个值。
- 线性探查 位置i被占用,探查i+1 i+2 … 装载因子过大
- 二次探查 位置i被占用,探查i+12 i-12 i+22 i-22 …
- 二度哈希 使用第1个哈希函数h1冲突时尝试使用h2,h3… 奇怪
- 拉链法 每个位置都链接一个链表,冲突发生时,冲突元素加到该位置链表的最后
拉链法
时间复杂度<O(n)
每个位置都链接一个链表,冲突发生时,冲突元素加到该位置链表的最后

# -- coding: utf-8 --
# @Project : algorithm
# @Time : 2022/6/5 17:38
# @Author : SIGNAL-01
# @File : hash_table.py
# @Software: PyCharm
class LinkList:
class Node:
def __init__(self, item=None):
self.item = item
self.next = None
class LinkListInterator:
def __init__(self, node):
self.node = node
def __next__(self):
if self.node:
cur_node = self.node
self.node = cur_node.next
return cur_node.item
else:
raise StopIteration
def __iter__(self):
return self
def __init__(self, iterable=None):
self.head = None
self.tail = None
if iterable:
self.extend(iterable)
def append(self, obj):
s = LinkList.Node(obj)
if not self.head:
self.head = s
self.tail = s
else:
self.tail.next = s
self.tail = s
def extend(self, iterable):
for obj in iterable:
self.append(obj)
def find(self, obj):
for n in self:
if n == obj:
return True
else:
return False
def __iter__(self):
return self.LinkListInterator(self.head)
def __repr__(self):
return "<<" + ",".join(map(str, self)) + ">>" # map指定映射 每一个对象self都转换成字符串str
# lk = LinkList([1.9, 2, 3])
# print(lk) # <<1.9,2,3>>
# for element in lk:
# print(element)
# # 1.9
# # 2
# # 3
class HashTable:
def __init__(self, size=101): # 哈希表长度
self.size = size
self.T = [LinkList() for _ in range(self.size)]
def h(self, k):
return k % self.size
def insert(self, k): # 插到i这个位置上
i = self.h(k)
if self.find(k): # 找到了/有值,不插入
print("Duplicated Insert")
else:
self.T[i].append(k)
def find(self, k):
i = self.h(k)
return self.T[i].find(k)
ht = HashTable()
ht.insert(0)
ht.insert(1)
ht.insert(3)
ht.insert(102)
ht.insert(508)
print(",".join(map(str, ht.T))) # <<0>>,<<1,102>>,<<>>,<<3,508>>,<<>>,<<>>,...
print(ht.find(102)) # True
print(ht.find(103)) # False
常见哈希函数:
- 除法哈希法
h(k)=k%m - 乘法哈希法
h(k)=floor(m*(A*key%1)) - 全域哈希法
ha.b(k)=((a*key b)mod p)mod m a,b=1,2,…,p-1
应用:集合与字典
- 字典与集合都是通过哈希表来实现的。
a {‘name’:‘Alex’,‘age’:18,‘gender’:‘Man’} - 使用哈希表存储字典,通过哈希函数将字典的键映射为下标。
假设h(‘name’)=3,h(‘age’)=1,h(‘gender’)=4,把value放到相应的位置上,则哈希表存储为[None,18,None,‘Alex’,‘Man’] - 多如果发生哈希冲突,则通过拉链法或开发寻址法解决
md5算法


SHA-2算法

应用 #比特币# #挖矿#

树
树是一种数据结构,比如:目录结构
树 是一种可以递归定义的 数据结构
模拟文件系统 (只有目录)
class Node:
def __init__(self, name, type='dir'):
self.name = name
self.type = type # "dir" or "file"
self.children = []
self.parent = None
def __repr__(self):
return self.name
# n = Node("hello")
# n2 = Node("world")
# n.children.append(n2)
# n2.parent = n
class FileSystemTree:
def __init__(self):
self.root = Node("/")
self.now = self.root
# 链式存储
def mkdir(self, name):
# name 以 / 结尾
if name[-1] != "/":
name += "/"
node = Node(name)
self.now.children.append(node)
node.parent = self.now
def ls(self): # 当前目录下的所有目录
return self.now.children
def cd(self, name): # 切换目录
if name[-1] != "/":
name += "/"
if name == "../":
self.now = self.now.parent
return
for child in self.now.children:
if child.name == name:
self.now = child
return
raise ValueError("invalid dir")
tree = FileSystemTree()
tree.mkdir("var/")
tree.mkdir("bin/")
tree.mkdir("usr/")
print(tree.root.children) # [var/, bin/, usr/]
print(tree.ls()) # [var/, bin/, usr/]
tree.cd("bin")
tree.mkdir("python/")
print(tree.ls()) # [python/]
tree.cd("../")
print(tree.ls()) # [var/, bin/, usr/]
二叉树 Binary Tree
二叉树的链式存储:将二叉树的节点定义为一个对象,节点之间通过类似链表的链接方式来连接。
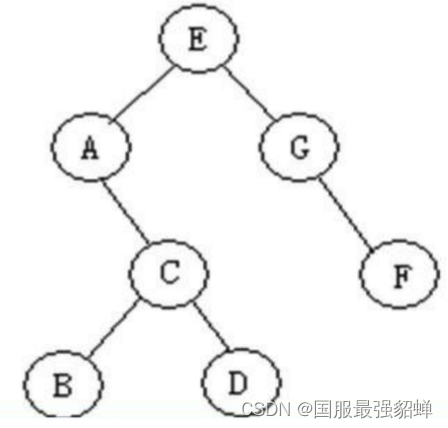
class BiTreeNode:
def __init__(self, data):
self.data = data
self.lchild = None
self.rchild = None
a = BiTreeNode("A")
b = BiTreeNode("B")
c = BiTreeNode("C")
d = BiTreeNode("D")
e = BiTreeNode("E")
f = BiTreeNode("F")
g = BiTreeNode("G")
e.lchild = a
e.rchild = g
a.rchild = c
c.lchild = b
c.rchild = d
g.rchild = f
root = e
print(root.lchild.rchild.data) # C
遍历
前序遍历 根 左子树 右子树
def pre_order(root):
if root:
print(root.data, end=',')
pre_order(root.lchild)
pre_order(root.rchild)
pre_order(root) # E,A,C,B,D,G,F,
中序遍历 左子树 根 右子树
def in_order(root):
if root:
in_order(root.lchild)
print(root.data, end=',')
in_order(root.rchild)
in_order(root) # A,B,C,D,E,G,F,
后序遍历 左子树 右子树 根
def post_order(root):
if root:
post_order(root.lchild)
post_order(root.rchild)
print(root.data, end=',')
post_order(root) # B,D,C,A,F,G,E,
层次遍历 需要用到队列
可用于多叉树
from collections import deque
def level_order(root):
queue = deque()
queue.append(root)
while len(queue) > 0:
node = queue.popleft()
print(node.data, end=',')
if node.lchild:
queue.append(node.lchild)
if node.rchild:
queue.append(node.rchild)
level_order(root) # E,A,G,C,F,B,D,
给两个遍历 求树
前序遍历 E,A,C,B,D,G,F
中序遍历 A,B,C,D,E,G,F
E是根节点,ABCD在左子树,GF在右子树
(ABCD)中,A是根节点,BCD在右子树
(BCD)中,C是根节点,B在左子树,D在右子树
(GF)中,G是根节点,R在右子树
二叉搜索树
中序序列一定是升序 左子树节点值 < 节点值 < 右子树节点值
时间复杂度: 查询O(logn) 插入O(logn) 删除(复杂)
平均情况时间复杂度O(logn)
最坏情况下,二叉搜索树可能非常偏斜
解决方案:随机化插入;AVL树
二叉搜索树 插入
class BiTreeNode:
def __init__(self, data):
self.data = data
self.lchild = None
self.rchild = None
self.parent = None
class BST:
def __init__(self, li=None):
self.root = None
if li:
for val in li:
# self.insert_rec(val)
self.insert_no_rec(val) # 因为递归执行效率较慢,所以使用非递归执行,因为再创建了另一个类,所以需要初始化一下树的根
def insert_rec(self, val): # 递归
if self.root is None:
self.root = BiTreeNode(val)
else:
self.insert(self.root, val)
def insert(self, node, val): # node 插入节点的位置 val 插入的值
if not node: # 如果树空 直接插入
node = BiTreeNode(val)
elif val < node.data:
node.lchild = self.insert(node.lchild, val)
node.lchild.parent = node
elif val > node.data:
node.rchild = self.insert(node.rchild, val)
node.rchild.parent = node
# else: # 默认 键不能相等/重复,查找也是只找到一个。键值对可加入一个新的count
return node
def insert_no_rec(self, val): # 非递归
p = self.root
if not p: # 空树
self.root = BiTreeNode(val)
return
while True:
if val < p.data: # 往左走
if p.lchild: # 左孩子存在
p = p.lchild
else: # 左孩子不存在
p.lchild = BiTreeNode(val)
p.lchild.parent = p
elif val > p.data: # 往右走
if p.rchild: # 右孩子存在
p = p.rchild
else: # 右孩子不存在
p.rchild = BiTreeNode(val)
p.rchild.parent = p
else: # 有值 不插入
return
def pre_order(self, root):
if root:
print(root.data, end=',')
self.pre_order(root.lchild)
self.pre_order(root.rchild)
def in_order(self, root):
if root:
self.in_order(root.lchild)
print(root.data, end=',')
self.in_order(root.rchild)
def post_order(self, root):
if root:
self.post_order(root.lchild)
self.post_order(root.rchild)
print(root.data, end=',')
tree = BST([4, 6, 7, 9, 2, 1, 3, 5, 8])
tree.pre_order(tree.root) # 4,2,1,3,6,5,7,9,8,
print('')
tree.in_order(tree.root) # 1,2,3,4,5,6,7,8,9,
print('')
tree.post_order(tree.root) # 1,3,2,5,8,9,7,6,4,
# 插入
# tree.insert_rec(10)
tree.insert_no_rec(10)
print('')
tree.in_order(tree.root) # 1,2,3,4,5,6,7,8,9,10
二叉搜索树 查询
二叉搜索树 删除
AVL树 至少要懂原理
自平衡的二叉搜索树
性质:根的左右子树高度之差(balance factor)的绝对值不超过1;根的左右子树都是平衡二叉树。
插入:插入节点可能会破坏avl树的平衡,需要旋转。
从下往上找第一个破坏平衡条件的节点。称为K。
不平衡的出现有4种情况。
左旋
右旋
右旋左旋
左旋右旋
AVL扩展:b树
自平衡的多路搜索树,常用于数据库索引
算法进阶
两种比较重要的算法思想:贪心算法,动态规划。
贪心:当前最好的选择。局部最优解。
不一定最优,某些问题是最优。
找零问题
背包问题 (01背包 分数背包)
拼接最大数字问题(面试经常出)
活动选择问题(也很经典)
最先结束的活动一定是最优解中的一部分。
O(n)
动态规划 dynamic programming
斐波那契数列 (递归 非递归)
DP的思想=递推式+重复子问题
钢条切割问题
自顶向下递归 O(2n)
自底向上 O(n2)
最长公共子序列
欧几里得算法
最大公约数GCD
gcd(a,b)=gcd(b,a mod b)
RSA加密算法(主流加密)
算法公开,密钥秘密
对称加密,非对称加密
为什么rsa加密算法解密不了(面试会问):两个质数相乘很容易,但一个很大的数拆成两个质数很难
学习记录,后面没再写