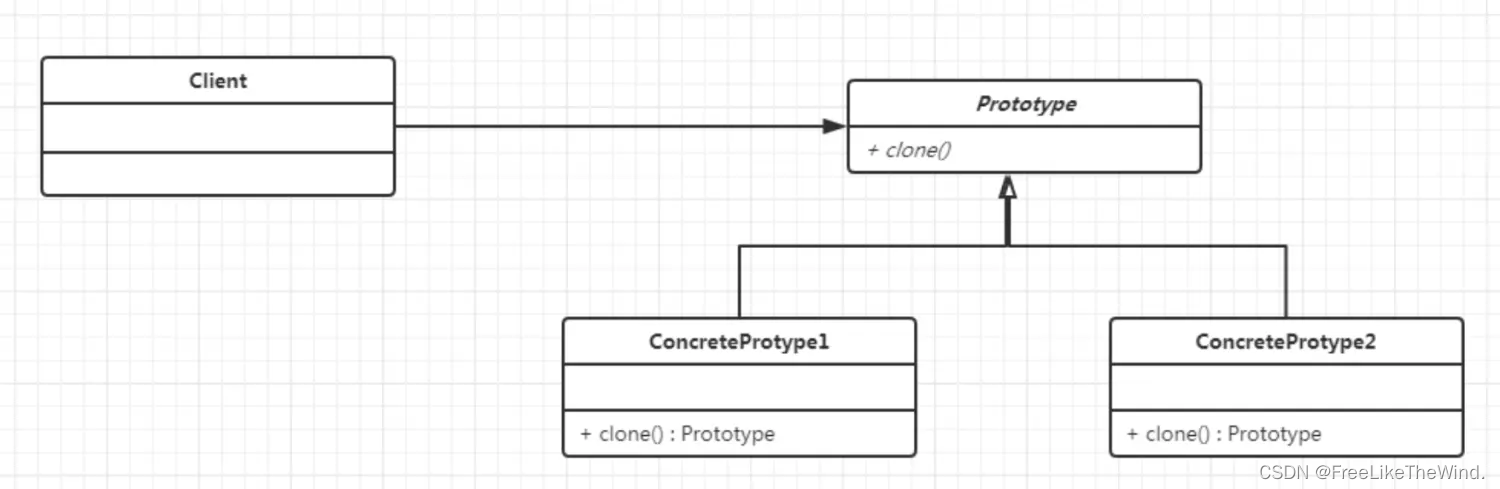
堆的基本概念
堆是一种特殊的树形数据结构,通常用于实现优先级队列。堆具有以下两个主要特点:
-
父节点的值始终大于或等于其子节点的值(最大堆),或者父节点的值始终小于或等于其子节点的值(最小堆)。
-
堆是一棵完全二叉树,这意味着所有层级除了最后一层都是完全填满的,最后一层从左到右填充。
最大堆和最小堆的定义
-
最大堆(Max Heap):在最大堆中,父节点的值始终大于或等于其子节点的值,这意味着根节点是堆中的最大元素。
-
最小堆(Min Heap):在最小堆中,父节点的值始终小于或等于其子节点的值,这意味着根节点是堆中的最小元素。
堆的常见操作
堆支持一些常见的操作,包括:
-
插入(Insertion):将新元素插入堆中,然后重新调整堆,以维护堆的性质。
-
删除(Deletion):删除堆中的根节点,然后重新调整堆,以维护堆的性质。
-
堆排序(Heap Sort):使用堆进行排序,将堆顶元素(最大或最小元素)与最后一个元素交换,然后减小堆的大小,并重新调整堆,重复此过程直到排序完成。
任务
堆在许多算法中都有广泛应用,包括Dijkstra算法、优先级队列等。掌握堆排序算法,这是一种高效的排序算法。
示例代码 - 使用C++创建最大堆和进行堆排序:
#include <iostream>
#include <vector>
#include <algorithm>
class MaxHeap {
public:
MaxHeap() {}
// 插入元素
void insert(int value) {
heap.push_back(value);
int index = heap.size() - 1;
heapifyUp(index);
}
// 删除最大元素
void removeMax() {
if (isEmpty()) {
return;
}
std::swap(heap[0], heap.back());
heap.pop_back();
heapifyDown(0);
}
// 堆排序
void heapSort() {
int n = heap.size();
for (int i = n / 2 - 1; i >= 0; i--) {
heapifyDown(i);
}
for (int i = n - 1; i > 0; i--) {
std::swap(heap[0], heap[i]);
heapifyDown(0, i);
}
}
// 判断堆是否为空
bool isEmpty() {
return heap.empty();
}
private:
std::vector<int> heap;
void heapifyUp(int index) {
while (index > 0) {
int parent = (index - 1) / 2;
if (heap[index] <= heap[parent]) {
break;
}
std::swap(heap[index], heap[parent]);
index = parent;
}
}
void heapifyDown(int index, int size = -1) {
if (size == -1) {
size = heap.size();
}
while (true) {
int leftChild = 2 * index + 1;
int rightChild = 2 * index + 2;
int largest = index;
if (leftChild < size && heap[leftChild] > heap[largest]) {
largest = leftChild;
}
if (rightChild < size && heap[rightChild] > heap[largest]) {
largest = rightChild;
}
if (largest == index) {
break;
}
std::swap(heap[index], heap[largest]);
index = largest;
}
}
};
int main() {
MaxHeap maxHeap;
maxHeap.insert(5);
maxHeap.insert(10);
maxHeap.insert(3);
maxHeap.insert(8);
maxHeap.insert(1);
std::cout << "堆排序前:";
for (int num : maxHeap) {
std::cout << num << " ";
}
maxHeap.heapSort();
std::cout << "\n堆排序后:";
for (int num : maxHeap) {
std::cout << num << " ";
}
return 0;
}
练习题:
-
解释堆的基本概念中的最大堆和最小堆的定义。
-
描述堆排序的步骤。
-
为什么堆可以用于高效的优先级队列实现?
-
在给定的一组元素中,如何创建一个最大堆?使用C++编写相应的代码。
-
在给定的一组元素中,如何使用堆排序进行排序?使用C++
解释堆的基本概念中的最大堆和最小堆的定义。
-
最大堆(Max Heap):在最大堆中,每个父节点的值都大于或等于其子节点的值。这意味着根节点包含堆中的最大元素。
-
最小堆(Min Heap):在最小堆中,每个父节点的值都小于或等于其子节点的值。这意味着根节点包含堆中的最小元素。
描述堆排序的步骤。
堆排序是一种原地、稳定的排序算法,它的步骤如下:
-
构建一个最大堆或最小堆,将数组视为堆。
-
不断从堆顶(最大值或最小值)移除元素,并将其放入已排序部分的末尾。
-
重复第二步,直到堆为空。
这个过程保证了每次移除的元素都是当前堆中的最大(最小)值,因此最终得到一个有序的数组。
为什么堆可以用于高效的优先级队列实现?
堆可以用于高效的优先级队列实现,因为堆的结构允许我们快速找到并删除最大(最小)元素,以及迅速插入新元素。这在许多算法和数据结构中都非常有用,如Dijkstra算法、Prim算法、任务调度等。堆的时间复杂度为O(log n),其中n是堆的大小,这使得优先级队列的操作非常高效。
在给定的一组元素中,如何创建一个最大堆?使用C++编写相应的代码。
创建最大堆的关键是从数组构建一个满足最大堆性质的堆。以下是使用C++创建最大堆的示例代码:
#include <iostream>
#include <vector>
void maxHeapify(std::vector<int>& arr, int size, int i) {
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
if (left < size && arr[left] > arr[largest]) {
largest = left;
}
if (right < size && arr[right] > arr[largest]) {
largest = right;
}
if (largest != i) {
std::swap(arr[i], arr[largest]);
maxHeapify(arr, size, largest);
}
}
void buildMaxHeap(std::vector<int>& arr) {
int size = arr.size();
for (int i = size / 2 - 1; i >= 0; i--) {
maxHeapify(arr, size, i);
}
}
int main() {
std::vector<int> arr = {4, 10, 3, 5, 1};
int size = arr.size();
buildMaxHeap(arr);
std::cout << "最大堆:";
for (int num : arr) {
std::cout << num << " ";
}
return 0;
}
运行结果:
在给定的一组元素中,如何使用堆排序进行排序?使用C++编写相应的代码。
堆排序的关键是将堆顶元素与数组末尾元素交换,然后减小堆的大小并重新调整堆。以下是使用C++进行堆排序的示例代码:
#include <iostream>
#include <vector>
void maxHeapify(std::vector<int>& arr, int size, int i) {
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
if (left < size && arr[left] > arr[largest]) {
largest = left;
}
if (right < size && arr[right] > arr[largest]) {
largest = right;
}
if (largest != i) {
std::swap(arr[i], arr[largest]);
maxHeapify(arr, size, largest);
}
}
void heapSort(std::vector<int>& arr) {
int size = arr.size();
for (int i = size / 2 - 1; i >= 0; i--) {
maxHeapify(arr, size, i);
}
for (int i = size - 1; i > 0; i--) {
std::swap(arr[0], arr[i]);
maxHeapify(arr, i, 0);
}
}
int main() {
std::vector<int> arr = {4, 10, 3, 5, 1};
int size = arr.size();
heapSort(arr);
std::cout << "堆排序结果:";
for (int num : arr) {
std::cout << num << " ";
}
return 0;
}
运行结果: