13 Scene planes and homographies
本章主要讲述两个摄像机和一个世界平面之间的射影几何关系。
我们假设空间有一平面 π \pi π,平面上的一点为 x π x_{\pi} xπ。 x π x_{\pi} xπ分别在两幅图像 P , P ′ P, P' P,P′上形成了 x , x ′ x, x' x,x′。
那么我们可以从两个方面来讨论:首先,从对极几何的角度来说,
x
x
x在
P
′
P'
P′上决定了一条直线,也就是极线。极线是由
x
x
x出发的射线在
P
′
P'
P′上投影形成的。第二,从homography角度来说,
x
x
x可以在
P
′
P'
P′上唯一确定一个点,因为从
x
x
x出发的射线和空间平面
π
\pi
π的交点可以求出来,也就是
x
π
x_{\pi}
xπ,知道了
x
π
x_{\pi}
xπ自然可以唯一确定
x
′
x'
x′。
文章目录
- 13 Scene planes and homographies
- 13.1 Homographies given the plane and vice versa
- 13.1.1 Homographies compatible with epipolar geometry
- 13.2 Plane induced homographies given F F F and image correspondences
- 13.2.1 Three points
- 13.2.2 A point and line
- 13.3 Computing F F F given the homography induced by a plane
- 13.4 The infinite homography H ∞ H_{\infin} H∞
13.1 Homographies given the plane and vice versa
现在我们来讨论一下单应性与平面之间的关系。空间内任意的一个平面可以唯一确定单应性,反之亦然。需要注意的是,空间内的平面不可以包括摄像机的光心,如果包括了光心,单应性就变成了退化的情况。
我们首先给出一个结论:
假设两个摄像机的投影矩阵分别是 P = [ I ∣ 0 ] , P ′ = [ A ∣ a ] P=[I|0],P'=[A|a] P=[I∣0],P′=[A∣a],空间内的平面表示为 π T X = 0 , π = ( V T , 1 ) \pi^T X = 0, \pi=(V^T, 1) πTX=0,π=(VT,1),由该平面确定的单应性就是 x ′ = H x x'=Hx x′=Hx,并且 H = A − a v T H = A-av^T H=A−avT。
13.1.1 Homographies compatible with epipolar geometry
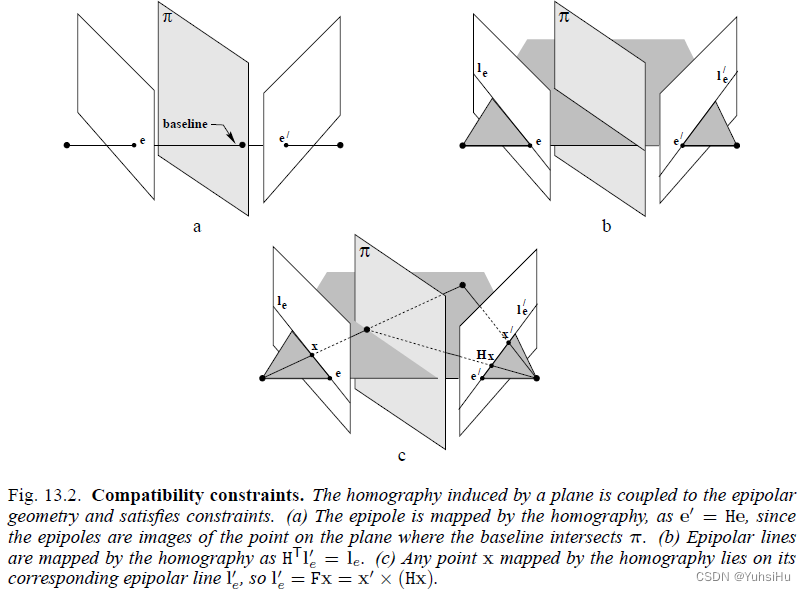
单应性与对极几何的关系。假设我们从空间平面上随机选择4个点,把他们投影到两幅图像,就会形成4对对应点。这4对对应点就确定了一个单应性矩阵 H H H。而且这4对对应点是满足对极几何约束的,i.e. x ′ T F x = 0 x'^T F x = 0 x′TFx=0。这种情况叫对极几何与单应性是相容(consistent or compatible)的。
假设我们从第一幅图像中随机选择四个点,第二幅图像也随机选四个点,可以利用它们计算出一个单应性矩阵,不一定能满足对极几何的约束,这种情况叫对极几何与单应性不相容。
现在我们考虑相容的情况。那么对应点之间可以表示为 x ↔ H x x \leftrightarrow Hx x↔Hx,带入对极几何的关系式,我们就得到 ( H x ) T F x = x T H T F x = 0 (Hx)^T F x = x^T H^T Fx = 0 (Hx)TFx=xTHTFx=0。
根据此式我们可以得出一个结论:
单应性矩阵
H
H
H与基本矩阵
F
F
F相容当且仅当
H
T
F
H^T F
HTF是一个斜对称矩阵(skew-symmetric),我们将其表达为:
H
T
F
+
F
T
H
=
0
H^T F + F^T H =0
HTF+FTH=0,
H
H
H的自由度是8-5=3。
由于以上关系是一个隐性的约束,我们接下来给出一个显式表达式。
结论 13.3
给出由两幅图像确定的基本矩阵 F F F,其对应的单应性矩阵 H H H可以表示为 H = A − e ′ V T H=A-e'V^T H=A−e′VT F = [ e ′ ] × A F=[e']_\times A F=[e′]×A。
引理 13.4
一个变换 H H H是两幅图像的单应矩阵当且仅当这两幅图像确定的 F F F可以分解成 [ e ′ ] × H [e']_\times H [e′]×H, e ′ e' e′是第二幅图像的极点。
根据以上介绍,我们知道单应性矩阵 H H H是由空间内某一平面 π \pi π确定的,那么在已知 H H H的情况下,我们如何求出平面 π \pi π?求解方程组 λ H = A − a v T \lambda H=A-av^T λH=A−avT就行。
13.2 Plane induced homographies given F F F and image correspondences
从基本矩阵和图像对应点来计算单应性矩阵。在前文我们是利用空间中的平面来计算单应性矩阵,在本节中我们直接从两幅图像中的对应元素来计算单应性矩阵。这是因为三维空间的平面可以用三个不共线的点来计算,或者用一条直线和一个点。这些元素都可以直接从两幅图中的对应元素推导出来。对应元素应该满足一些性质:
- 对应元素要满足对极几何的约束
- 三维空间中的元素会出现退化的情况,这是因为元素之间共面或者共线
我们首先讨论从三个对应点来计算单应性矩阵的情况。
13.2.1 Three points
假设我们知道空间中的三个点 X i X_i Xi在两幅图像上形成的投影,并且我们已知基本矩阵 F F F,我们可以这样计算单应矩阵 H H H:
首先空间点 X i X_i Xi的坐标可以计算出来(12章的三角化),知道了三个点的位置,那么它们所在的平面就可以被计算出来(3.3-P66),已知平面就可以根据13.1节的方法来计算 H H H,这种方法叫显式法。
其次,我们也可以用四个点来计算 H H H,第四个点就是极点。所以我们可以有这样的方程组: x ′ = H x , e ′ = H e x'=Hx, e'=He x′=Hx,e′=He,这种方法叫隐式法。
那么这两种方法有啥区别?我们应该用哪一种?答案是我们应该用显示法,因为隐式法包含了退化的情况。为什么呢?因为如果有两个点和极点共线,那么 H H H就算不出来了,参见4.1.3 P91。同时,如果点和极点几乎共线,那么隐式法会给出一个非常差的结果,但是显式法没有这个问题,它可以处理点和极点共线的情况。
我们下面来形式化的表示一下。
结论13.6 给定一个基本矩阵 F F F和三对对应点 x i ↔ x i ′ x_i \leftrightarrow x'_i xi↔xi′,由这三对点所在平面构成的 H H H可以表达为: H = A − e ′ ( M − 1 b ) T H=A-e'(M^{-1}b)^T H=A−e′(M−1b)T。
A = [ e ′ ] × F A=[e']_\times F A=[e′]×F b b b是一个三维向量,每一维可以表达成:
b i = ( x i ′ × ( A x i ) ) T ( x i ′ × e ′ ) / ∣ ∣ x i ′ × e ′ ∣ ∣ 2 b_i = (x'_i \times (Ax_i))^T (x'_i \times e')/||x'_i \times e'||^2 bi=(xi′×(Axi))T(xi′×e′)/∣∣xi′×e′∣∣2
M M M是 3 × 3 3 \times 3 3×3的矩阵, 每一行是 x i T x_i^T xiT。
一致性条件 每一对对应点都会对 H H H增加一个约束,该约束可以表达为: e ′ × x i ′ = e ′ × A x i = F x i e' \times x'_i = e' \times Ax_i = Fx_i e′×xi′=e′×Axi=Fxi,这个等式左边 e ′ × x i ′ e' \times x'_i e′×xi′的几何意义是通过 x i ′ x'_i xi′的极线,右边 F x i F x_i Fxi就是 x i x_i xi在第二幅图像中的极线。所以整个式子的意思就是 x i ′ x'_i xi′在 x i x_i xi对应的极线上。
存在噪声的情况 一般情况下图像中都包含噪声,那么我们就用迭代的方法来优化 x , x ′ x,x' x,x′的位置(12.1节P318),然后用12.6节的极大似然估计来求3D空间点的坐标和 H H H。
13.2.2 A point and line
点和线来估计 H H H。本节先将线对应关系,再讲点对应关系。
线对应 两幅图像中的对应线确定了三维空间中的一条对应线。三维空间中的线位于一族平面上(不是一个平面)。这一族平面对应于一族 H H H。
结论 13.7 由一对对应直线 l ↔ l ′ l \leftrightarrow l' l↔l′ 确定的一族平面对应了一族单应性矩阵 H H H,它可以表达为
H ( μ ) = [ l ′ ] × F + μ e ′ l T H(\mu) = [l']_{\times} F + \mu e'l^T H(μ)=[l′]×F+μe′lT
从这个式子我们可以看出, H H H只取决于 μ \mu μ这一个参数。我们回忆一下13.1节, H H H同样有一个表达式,该表达式是在已知两个摄像机矩阵 P = K [ I ∣ 0 ] , P ′ = K ′ [ R ∣ t ] P=K[I|0],P'=K'[R|t] P=K[I∣0],P′=K′[R∣t] 和空间平面 π = ( n T , d ) T \pi=(n^T,d)^T π=(nT,d)T的情况下给出的。
H = K ′ ( R − t n T / d ) K − 1 H=K'(R-tn^T/d)K^{-1} H=K′(R−tnT/d)K−1
这个式子由三个参数决定,因为 n T n^T nT是一个三维向量。对比上文的两个式子,我们可以看出由直线确定的 H H H只需要一个参数,由平面确定的 H H H需要三个参数,也就是说直线将参数的维度从3压缩到了1。
线和点的对应 从上文我们知道线对应关系可以确定 H ( μ ) H(\mu) H(μ),那么怎么确定 μ \mu μ的取值呢?我们用点对应 x ↔ x ′ x \leftrightarrow x' x↔x′ 来确定。
结论13.8 已知 F F F和一对对应点 x ↔ x ′ x \leftrightarrow x' x↔x′,一对对应线 l ↔ l ′ l \leftrightarrow l' l↔l′, H H H可以表达为如下式子:
H = [ l ′ ] × F + ( x ′ × e ′ ) T ( x ′ × ( ( F x ) × l ′ ) ) ∣ ∣ x ′ × e ′ ∣ ∣ 2 ( l T x ) e ′ l T H=[l']_{\times} F + \frac{(x' \times e')^T(x' \times ((Fx) \times l'))} {||x' \times e'||^2 (l^Tx)} e'l^T H=[l′]×F+∣∣x′×e′∣∣2(lTx)(x′×e′)T(x′×((Fx)×l′))e′lT
应用这个公式的前提是 x , x ′ x, x' x,x′得满足对极几何约束,那么在有噪声的情况下,我们首先就得用算法12.1(P318)先优化一下。
H
(
μ
)
H(\mu)
H(μ)的几何解释
H
(
μ
)
H(\mu)
H(μ)首先满足
x
=
H
(
μ
)
x
′
x=H(\mu)x'
x=H(μ)x′。我们将
H
(
μ
)
H(\mu)
H(μ)的表达式带入,可以得到:
x
′
=
H
(
μ
)
x
=
(
[
l
′
]
×
F
+
μ
e
′
l
T
)
x
=
[
l
′
]
×
F
x
x'=H(\mu)x = ([l']_{\times} F + \mu e'l^T)x = [l']_{\times}Fx
x′=H(μ)x=([l′]×F+μe′lT)x=[l′]×Fx
最后得到的结果跟 μ \mu μ没关系,只和 F F F有关系。所以我们说对极几何为 l ↔ l ′ l \leftrightarrow l' l↔l′上的每一点都确定了对应关系。这个结论很显然。因为 F F F本来就是描述两幅图像上点对应关系的,只不过现在的点都在 l , l ′ l, l' l,l′上了。
退化的单应矩阵 如果说三维空间中的平面包括了摄像机的光心,那么 H H H就属于退化的情况。在退化情况下 H H H就不是满秩矩阵,如果 r a n k ( H ) = 2 rank(H)=2 rank(H)=2, H H H投影结果就是一条直线。 r a n k ( H ) = 1 rank(H) = 1 rank(H)=1, H H H投影结果就是一个点。如果我们从 H ( μ ) H(\mu) H(μ)的情况考虑,那么退化就可以表达成 μ → inf \mu \rightarrow \inf μ→inf或者 μ → 0 \mu \rightarrow 0 μ→0。
13.3 Computing F F F given the homography induced by a plane
我们讨论如何在已知 H H H的情况下求解 F F F。前几章我们讲述的是已知 F F F,怎么求解 H H H。现在我们反过来,求已知 H H H的情况下,如何求解 F F F。
主要思路就是构造一个平面 π \pi π, X X X不在 π \pi π上。那么 x x x和 π \pi π有一个交点 x π x_{\pi} xπ,该交点向 P ′ P' P′投影,得到 x ~ ′ \tilde{x}' x~′。 x ~ ′ \tilde{x}' x~′肯定和 x ′ x' x′不一样,除非 X X X在 π \pi π上。那么我们用 x ~ ′ , x ′ \tilde{x}', x' x~′,x′做叉乘,得到的线段肯定过极点 e ′ e' e′,再找另外一个 x ~ ′ \tilde{x}' x~′,重复一遍,就得到第二条过极点 e ′ e' e′的极线,两个极线交点就是极点 e ′ e' e′,知道了 e ′ e' e′,就可以用 [ e ′ ] × H = F [e']_{\times} H =F [e′]×H=F求出 F F F。
所以最简单的办法就是找出6对对应点,其中有4对共面的。用这4对点来计算 H H H (求解方程组 x i ′ = H x i x'_i=Hx_i xi′=Hxi),然后用 x 5 , x 6 x_5,x_6 x5,x6求出两条直线 ( H x 5 ) × x 5 ′ (Hx_5) \times x'_5 (Hx5)×x5′, ( H x 6 ) × x 6 ′ (Hx_6) \times x'_6 (Hx6)×x6′,两个直线做叉乘就是极点 e ′ e' e′, 所以 F = [ e ′ ] × H F=[e']_{\times} H F=[e′]×H。
投影点的深度
一个世界平面内的点
X
=
(
x
T
,
ρ
)
T
X=(x^T,\rho)^T
X=(xT,ρ)T投影在第一幅图像上形成了
x
x
x,第二幅图像上形成了
x
′
=
H
x
+
ρ
e
′
x'=Hx+\rho e'
x′=Hx+ρe′,根据上一节的模型,我们知道
x
′
,
e
′
H
x
x', e' Hx
x′,e′Hx三点共线。
ρ
\rho
ρ可以被看做偏离
H
H
H相对程度的一个指标,那么它就可以被认为是
X
X
X与平面
π
\pi
π之间的距离。
ρ
=
0
\rho=0
ρ=0表明
X
X
X在平面
π
\pi
π上
ρ
\rho
ρ的符号就可以表明
X
X
X位于平面的哪一边。
两个平面求F
假设我们知道两个平面
π
1
,
π
2
\pi_1,\pi_2
π1,π2,那么他们确定两个单应矩阵
H
1
,
H
2
H_1,H_2
H1,H2。这两个单应矩阵足以确定
F
F
F,其实他们是超定了。我们可以构造一个矩阵
H
=
H
2
H
1
H=H_2 H_1
H=H2H1,这是第一幅图像到自己的映射。那么极点
e
e
e在
H
H
H的映射下是不变的。那么
F
=
[
e
′
]
×
H
i
,
i
=
1
,
2
,
e
′
=
H
i
e
F=[e']_{\times} H_i, i=1,2, e'=H_ie
F=[e′]×Hi,i=1,2,e′=Hie,
H
H
H的另外一个性质是有相同的两个特征值。因为
H
1
,
H
2
H_1,H_2
H1,H2在空间中会相交,然后形成一条直线。这个直线往第一幅图像中投影,得到的投影直线在
H
H
H的映射下是不变的。所以这个
H
H
H有一条固定的直线,还有一个固定点也就是极点
e
e
e。
13.4 The infinite homography H ∞ H_{\infin} H∞
无穷远处的单应矩阵。
定义 13.10 H ∞ H_{\infty} H∞ 是由无穷远处平面 π ∞ \pi_{\infty} π∞定义的单应矩阵。
我们回忆参数化的
H
H
H表达式
H
=
K
′
(
R
−
t
n
T
/
d
)
K
−
1
H=K'(R-tn^T/d)K^{-1}
H=K′(R−tnT/d)K−1(由三个参数确定),那么
H
∞
=
lim
d
→
∞
H
=
K
′
R
K
−
1
H_{\infty} = \lim_{d \to \infty} H = K'RK^{-1}
H∞=d→∞limH=K′RK−1
由上式可以看出 H ∞ H_{\infty} H∞ 并不依赖于图像之间的平移,只和旋转、内参有关系。
如果我们考虑两幅图之间对应的点,我们可以由下式:
x
′
=
K
′
R
K
−
1
+
K
′
t
/
Z
=
H
∞
x
+
K
′
t
/
Z
x'=K'RK^{-1} + K't/Z = H_{\infty} x + K't/Z
x′=K′RK−1+K′t/Z=H∞x+K′t/Z
Z Z Z就是点相对于第一幅图像的深度。从上式中我们可以看出无穷远处的点( z = ∞ z=\infty z=∞)是由 H ∞ H_{\infty} H∞映射到图像上的。如果平移 t t t是零,那么我们就可以得到 H ∞ H_{\infty} H∞,这相当与摄像机绕自己光心进行旋转。所以如果摄像机绕自己光心进行旋转,那么 H ∞ H_{\infty} H∞就是关于图像上任意深度点的一个单应矩阵。
如果我们考虑到
e
′
=
K
′
t
e'=K't
e′=K′t那么
x
′
=
H
∞
x
+
e
′
/
z
x'=H_{\infty}x+e'/z
x′=H∞x+e′/z,我们对比书中式13.9
x
′
=
H
x
+
ρ
e
′
x'=Hx+\rho e'
x′=Hx+ρe′可以看出来
1
/
z
1/z
1/z就相当于
ρ
\rho
ρ,所以说逆深度可以解释为点相对于无穷远平面
π
∞
\pi_{\infty}
π∞的距离。
消失点和消失线
无穷远处平面上的点是由
H
∞
H_{\infty}
H∞映射到图像上的,这些点就是消失点。所以
H
∞
H_{\infty}
H∞在两幅图像中的消失点
v
′
,
v
v', v
v′,v之间建立了映射
v
′
=
H
v
v'=Hv
v′=Hv,所以
H
∞
H_{\infty}
H∞可以由三个不共线的消失点计算,也可以由对应的消失线计算(13.2.2节)。
仿射重建和度量重建
回忆chapter 10,知道了无穷远平面
π
∞
\pi_{\infty}
π∞可以把投影重建升级成度量重建。
H
∞
H_{\infty}
H∞会出现在重建过程中,因为我们如果指定
P
=
[
I
∣
0
]
,
P
′
=
[
H
∞
∣
λ
e
′
]
P=[I|0],P'=[H_{\infty}|\lambda e']
P=[I∣0],P′=[H∞∣λe′],重建过程就是仿射重建。
假设我们规定 π ∞ \pi_{\infty} π∞的坐标是 ( 0 , 0 , 0 , 1 ) (0,0,0,1) (0,0,0,1), H ∞ H_{\infty} H∞可以直接从摄像机矩阵中来决定。我们假设 P = [ M ∣ 0 ] , P ′ = [ M ′ ∣ t ] P=[M|0], P'=[M'|t] P=[M∣0],P′=[M′∣t],那么无穷远平面上的一点 X = ( x ∞ T , 0 ) T X=(x^T_{\infty},0)^T X=(x∞T,0)T就会被映射到 x = P X = M x ∞ , x ′ = P ′ X = M ′ x ∞ x=PX=Mx_{\infty}, x'=P'X=M'x_{\infty} x=PX=Mx∞,x′=P′X=M′x∞,所以 x ′ = M ′ M − 1 x'=M'M^{-1} x′=M′M−1, 那么 H i n f t y = M ′ M − 1 H_{infty} = M'M^{-1} Hinfty=M′M−1。
H ∞ H_{\infty} H∞还可以被用来进行两个相机之间的标定。假设 π ∞ \pi_{\infty} π∞上的绝对圆 Ω ∞ \Omega_{\infty} Ω∞映射在两个图像上,分别表示为 ω , ω ′ \omega, \omega' ω,ω′,他们之间存在如下关系: ω ′ = H ∞ − T ω H ∞ − 1 \omega'=H_{\infty}^{-T} \omega H_{\infty}^{-1} ω′=H∞−TωH∞−1,那么我们如果知道 ω \omega ω,就可以计算 ω ′ \omega' ω′,然后分解它,就知道了第二个相机的内参。
立体匹配
H
∞
H_{\infty}
H∞还可以用来缩小立体匹配时极线搜索的范围。因为
x
x
x和无穷远平面由一个交点,记为
X
∞
X_{\infty}
X∞,它往图像二上投影,得到
x
∞
′
x'_{\infty}
x∞′,那么与
x
x
x匹配的
x
′
x'
x′肯定位于
e
′
e'
e′与
x
∞
′
x'_{\infty}
x∞′ 之间,所以我们不用搜索整个极线。