文章目录
- 红黑树
- 1.简介
- 2.为什么需要红黑树?
- 3.性质
- 4. 红黑树的效率
- 4.1 红黑树效率
- 4.2 红黑树和AVL树的比较
- 5.AVL树 vs 红黑树
- 5.1 AVL树
- 5.2 红黑树
- 5.3 如何选择
红黑树

1.简介
红黑树是一种自平衡的二叉查找树,是一种高效的查找树。它是由 Rudolf Bayer 于1972年发明,在当时被称为对称二叉 B 树(symmetric binary B-trees)。后来,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的红黑树。
红黑树具有良好的效率,它可在 O(logN) 时间内完成查找、增加、删除等操作。因此,红黑树在业界应用很广泛,比如 Java 中的 TreeMap,JDK 1.8 中的 HashMap、C++ STL 中的 map 均是基于红黑树结构实现的。
考虑到红黑树是一种被广泛应用的数据结构,所以我们很有必要去弄懂它。
2.为什么需要红黑树?
对于二叉搜索树,如果插入的数据是随机的,那么它就是接近平衡的二叉树,平衡的二叉树,它的操作效率(查询,插入,删除)效率较高,时间复杂度是O(logN)。但是可能会出现一种极端的情况,那就是插入的数据是有序的(递增或者递减),那么所有的节点都会在根节点的右侧或左侧,此时,二叉搜索树就变为了一个链表,它的操作效率就降低了,时间复杂度为O(N),所以可以认为二叉搜索树的时间复杂度介于O(logN)和O(N)之间,视情况而定。那么为了应对这种极端情况,红黑树就出现了,它是具备了某些特性的二叉搜索树,能解决非平衡树问题,红黑树是一种接近平衡的二叉树(说它是接近平衡因为它并没有像AVL树的平衡因子的概念,它只是靠着满足红黑节点的5条性质来维持一种接近平衡的结构,进而提升整体的性能,并没有严格的卡定某个平衡因子来维持绝对平衡)。
3.性质
学过二叉查找树的同学都知道,普通的二叉查找树在极端情况下可退化成链表,此时的增删查效率都会比较低下。
为了避免这种情况,就出现了一些自平衡的查找树,比如 AVL,红黑树等。这些自平衡的查找树通过定义一些性质,将任意节点的左右子树高度差控制在规定范围内,以达到平衡状态。
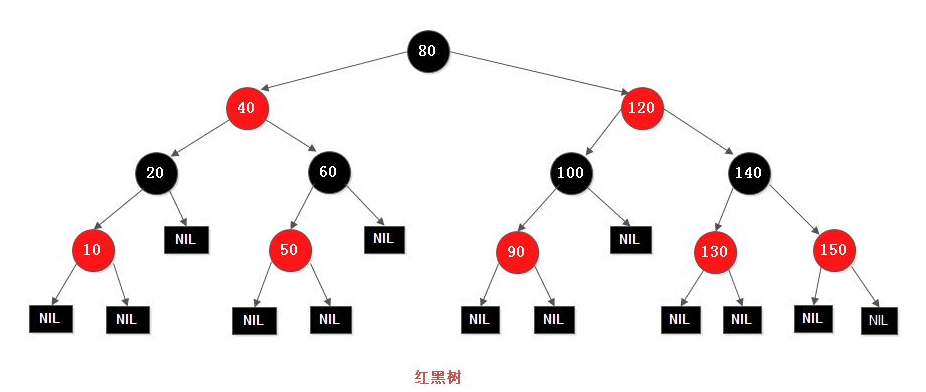
以红黑树为例,红黑树通过如下的性质定义实现自平衡:
- 节点是红色或黑色。
- 根是黑色。
- 所有叶子都是黑色(叶子是NIL节点)。
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点(简称黑高)。
有了上面的几个性质作为限制,即可避免二叉查找树退化成单链表的情况。
但是,仅仅避免这种情况还不够,这里还要考虑某个节点到其每个叶子节点路径长度的问题。
如果某些路径长度过长,那么,在对这些路径上的及诶单进行增删查操作时,效率也会大大降低。
这个时候性质4和性质5用途就凸显了,有了这两个性质作为约束,即可保证任意节点到其每个叶子节点路径最长不会超过最短路径的2倍。原因如下:
当某条路径最短时,这条路径必然都是由黑色节点构成。当某条路径长度最长时,这条路径必然是由红色和黑色节点相间构成(性质4限定了不能出现两个连续的红色节点)。而性质5又限定了从任一节点到其每个叶子节点的所有路径必须包含相同数量的黑色节点。
此时,在路径最长的情况下,路径上红色节点数量 = 黑色节点数量。该路径长度为两倍黑色节点数量,也就是最短路径长度的2倍。
4. 红黑树的效率
4.1 红黑树效率
红黑树的查找,插入和删除操作,时间复杂度都是O(logN)。
查找操作时,它和普通的相对平衡的二叉搜索树的效率相同,都是通过相同的方式来查找的,没有用到红黑树特有的特性。
但如果插入的时候是有序数据,那么红黑树的查询效率就比二叉搜索树要高了,因为此时二叉搜索树不是平衡树,它的时间复杂度O(N)。
插入和删除操作时,由于红黑树的每次操作平均要旋转一次和变换颜色,所以它比普通的二叉搜索树效率要低一点,不过时间复杂度仍然是O(logN)。
总之,红黑树的优点就是对有序数据的查询操作不会慢到O(logN)的时间复杂度。
4.2 红黑树和AVL树的比较
- AVL树的时间复杂度虽然优于红黑树,但是对于现在的计算机,cpu太快,可以忽略性能差异
- 红黑树的插入删除比AVL树更便于控制操作
- 红黑树整体性能略优于AVL树(红黑树旋转情况少于AVL树)
5.AVL树 vs 红黑树
5.1 AVL树
- 平衡标准比较严格:每个左右子树的高度差不超过1
- 最大高度是 1.44 ∗ log2 n + 2 − 1.328(100W个节点,AVL树最大树高28)
- 搜索、添加、删除都是 O(logn) 复杂度,其中添加仅需 O(1) 次旋转调整、删除最多需要 O(logn) 次旋转调整
5.2 红黑树
- 平衡标准比较宽松:没有一条路径会大于其他路径的2倍
- 最大高度是 2 ∗ log2(n + 1)( 100W个节点,红黑树最大树高40)
- 搜索、添加、删除都是 O(logn) 复杂度,其中添加、删除都仅需 O(1) 次旋转调整
5.3 如何选择
- 搜索的次数远远大于插入和删除,选择AVL树;搜索、插入、删除次数几乎差不多,选择红黑树
- 相对于AVL树来说,红黑树牺牲了部分平衡性以换取插入/删除操作时少量的旋转操作,整体来说性能要优于AVL树
- 红黑树的平均统计性能优于AVL树,实际应用中更多选择使用红黑树
资料来源:
1、【数据结构】史上最好理解的红黑树讲解,让你彻底搞懂红黑树_小七mod的博客-CSDN博客
2、一文带你彻底读懂红黑树(附详细图解) - 知乎 (zhihu.com)







![C/C++:[Error] ld returned 1 exit status 解决方案](https://img-blog.csdnimg.cn/de1daf8b8b7f4ec3bc2148f029061a1a.png)