wy的leetcode刷题记录_Day59
声明
本文章的所有题目信息都来源于leetcode
如有侵权请联系我删掉!
时间:2022-12-9
前言
目录
- wy的leetcode刷题记录_Day59
- 声明
- 前言
- 1780. 判断一个数字是否可以表示成三的幂的和
- 题目介绍
- 思路
- 代码
- 收获
- 63. 题目
- 题目介绍
- 思路
- 代码
- 收获
1780. 判断一个数字是否可以表示成三的幂的和
今天的每日一题是:1780. 判断一个数字是否可以表示成三的幂的和
题目介绍
给你一个整数 n ,如果你可以将 n 表示成若干个不同的三的幂之和,请你返回 true ,否则请返回 false 。
对于一个整数 y ,如果存在整数 x 满足 y == 3x ,我们称这个整数 y 是三的幂。
示例 1: 输入:n = 12
输出:true
解释:12 = 31 + 32
示例 2:
输入:n = 91
输出:true
解释:91 = 30 + 32 + 34
思路
方法一:分析题目,可知本题是求y是否能被不同的三的幂的和组成。y的取值在10的七次方范围内,小于3的二十次方。于是我选择使用一个数组来存3的0-19次方的值,然后根据贪心法,从后向前遍历,判断其是否能为符合题意的组成条件。最后判断选择的数的和是否为y即可。(其实这里还可以再简化一下,不用规定20次方这么死,y的值小于3的n次方时,用这个n即可)。
方法二(参考题解):数学分析法:我们可以将y看做成三进制表示,我们知道三进制表示的数每一个数位上的值表示多少个这个数位次方组成,当这个数字是0和1的时候是被允许的,而2的时候就不符合题意了(若干个不同…),所以我们仅需要判断三进制组成中的每一个数位是否出现2,如果是2那么返回false,如果不是那么返回true。
代码
贪心法:
class Solution {
public:
bool checkPowersOfThree(int n) {
// if(n%3!=0)
// return false;
int loop_num=20;
vector<int> quare_3(loop_num);
for(int i=0;i<loop_num;i++)
{
quare_3[i]=pow(3,i);
}
int temp=loop_num-1;
while(n!=0)
{
if(n>=quare_3[temp])
{
n-=quare_3[temp];
}
temp--;
if(temp==-1)
break;
}
if(n==0)
return true;
return false;
}
};
数学分析法:
class Solution {
public:
bool checkPowersOfThree(int n) {
while(n!=0)
{
if(n%3==2)
return false;
n/=3;
}
return true;
}
};
收获
稍微复杂一点的模拟题,采用了一点模拟思路。
63. 题目
450. 删除二叉搜索树中的节点
题目介绍
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点;
如果找到了,删除它。
示例 1:
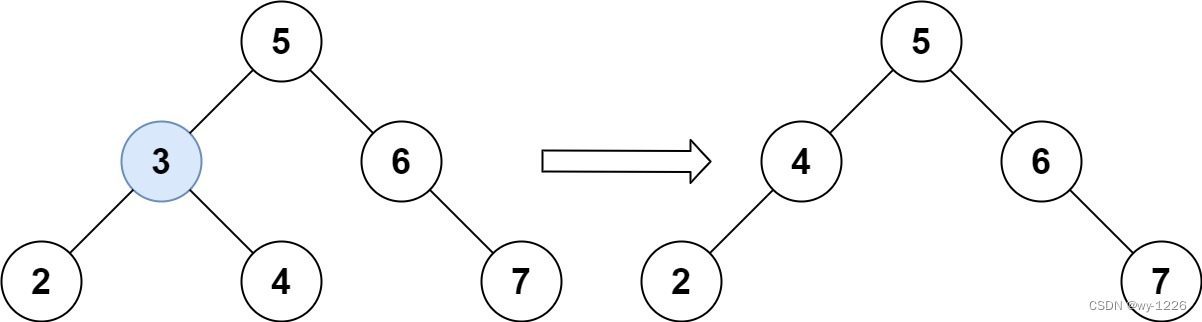
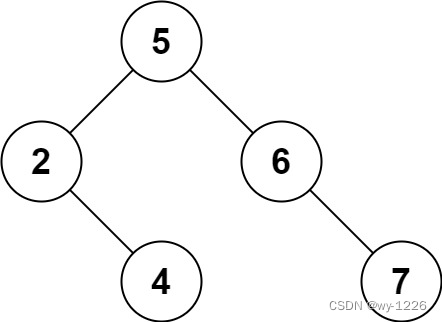
输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。 一个正确的答案是
[5,4,6,2,null,null,7], 如下图所示。 另一个正确答案是 [5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
思路
对于搜索二叉树,我们首先寻找到要删除的节点(这一点很容易),然后对于这个要删除的节点我们要讨论四种情况:1、该节点是叶子节点那么直接删除。2、该节点没有左节点,那么返回右节点。3、该节点没有右节点,那么返回左节点。4、该节点既有左节点又有右节点,那么我们有俩种方法这里我们只说其中一种,我们将该节点的左子树加入到该节点的右子树中的最左边的节点的左节点。
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if(!root)
{
return nullptr;
}
if(root->val==key)
{
if(root->left==nullptr)
return root->right;
else if(root->right==nullptr)
return root->left;
else
{
TreeNode *curr=root->right;
while(curr->left!=nullptr)
{
curr=curr->left;
}
curr->left=root->left;
TreeNode* temp=root;
root=root->right;
delete temp;
return root;
}
}
else if(root->val>key)
{
root->left=deleteNode(root->left,key);
}
else if(root->val<key)
{
root->right=deleteNode(root->right,key);
}
return root;
}
};
收获
掌握了删除子树的逻辑及其实现。








![[论文阅读] SqueezeSeg V1](https://img-blog.csdnimg.cn/b6c8f3c4bbe64aad88f9089dbdd848a5.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAd29sZl9raW5nXzU4Ng==,size_17,color_FFFFFF,t_70,g_se,x_16)