图的基本概念
图是一种数据结构,用于表示对象之间的关系。它由两个基本组件构成:
-
顶点(Vertex):也被称为节点,代表图中的对象或实体。
-
边(Edge):连接两个顶点的线,表示顶点之间的关系。
有向图和无向图的区别
图可以分为两种主要类型:
-
无向图(Undirected Graph):边没有方向,表示两个顶点之间的关系是双向的。想象你和朋友之间的社交网络关系图,这就是一个无向图的例子。
-
有向图(Directed Graph):边有方向,表示从一个顶点到另一个顶点的关系是单向的。一个典型的有向图示例是网页链接图,其中箭头表示链接方向。
图的遍历方法
遍历图意味着访问图中的所有顶点和边。两种常见的图遍历方法如下:
-
深度优先搜索(DFS):DFS从起始顶点开始,沿着一条路径尽可能深入,直到无法继续为止,然后回溯到其他路径。这种方法类似于探险,一直往前走直到没有未探索的路径。
-
广度优先搜索(BFS):BFS从起始顶点开始,首先访问所有直接相邻的顶点,然后逐层向外扩展。这种方法类似于水波扩散,先探索离起点最近的区域,然后逐渐扩展到更远的区域。
任务
创建和操作图数据结构,以及理解图的遍历算法。
示例代码 - 使用C++创建简单的无向图:
#include <iostream>
#include <vector>
class Graph {
public:
Graph(int vertices) : V(vertices) {
adj = std::vector<std::vector<int>>(vertices);
}
void addEdge(int v, int w) {
adj[v].push_back(w);
adj[w].push_back(v);
}
void printGraph() {
for (int v = 0; v < V; ++v) {
std::cout << "顶点 " << v << " 的邻居: ";
for (const int& neighbor : adj[v]) {
std::cout << neighbor << " ";
}
std::cout << std::endl;
}
}
private:
int V; // 顶点数
std::vector<std::vector<int>> adj; // 邻接表
};
int main() {
Graph g(5); // 创建一个具有5个顶点的图
// 添加边
g.addEdge(0, 1);
g.addEdge(0, 4);
g.addEdge(1, 2);
g.addEdge(1, 3);
g.addEdge(1, 4);
g.addEdge(2, 3);
g.addEdge(3, 4);
// 打印图的邻接表
g.printGraph();
return 0;
}
运行结果: 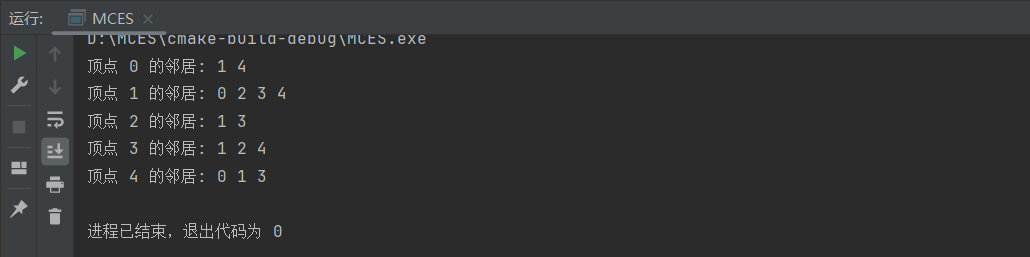
练习题:
-
解释图的基本概念中的顶点和边。
-
什么是有向图和无向图?可以给出一个实际生活中的例子吗?
-
描述深度优先搜索(DFS)和广度优先搜索(BFS)的工作原理。
-
你可以设计一个简单的图,表示你和你的朋友之间的社交关系。使用C++创建这个图并实现DFS或BFS来查找朋友之间的关系路径。
解释图的基本概念中的顶点和边。
-
顶点:顶点也被称为节点,它们是图中的基本元素,代表对象或实体。在社交网络中,每个人可以被表示为一个顶点。
-
边:边是连接两个顶点的线,表示顶点之间的关系。在社交网络中,如果两个人是朋友关系,就可以用一条边来表示这种关系。
什么是有向图和无向图?可以给出一个实际生活中的例子吗?
-
有向图:有向图中,边有方向,表示从一个顶点到另一个顶点的关系是单向的。例如,Twitter中的关注关系就是一个有向图,其中用户A关注了用户B,但不一定反过来成立。
-
无向图:无向图中,边没有方向,表示两个顶点之间的关系是双向的。例如,Facebook的好友关系可以用无向图表示,如果用户A是用户B的好友,那么用户B也是用户A的好友。
描述深度优先搜索(DFS)和广度优先搜索(BFS)的工作原理。
-
DFS(深度优先搜索):DFS从起始顶点开始,沿着一条路径尽可能深入,直到无法继续为止,然后回溯到其他路径。它使用栈数据结构或递归来实现。DFS类似于沿着分支往下走直到底部,然后再返回并探索其他分支。
-
BFS(广度优先搜索):BFS从起始顶点开始,首先访问所有直接相邻的顶点,然后逐层向外扩展。它使用队列数据结构来实现。BFS类似于水波扩散,先探索离起点最近的区域,然后逐渐扩展到更远的区域。
你可以设计一个简单的图,表示你和你的朋友之间的社交关系。使用C++创建这个图并实现DFS或BFS来查找朋友之间的关系路径。
这是一个简单的C++示例代码,一个社交关系图并执行DFS来查找朋友之间的关系路径。请注意,这只是一个示例,实际应用中的社交关系图通常更复杂。
#include <iostream>
#include <vector>
#include <queue>
class Graph {
public:
Graph(int vertices) : V(vertices) {
adj = std::vector<std::vector<int>>(vertices);
}
void addEdge(int v, int w) {
adj[v].push_back(w);
adj[w].push_back(v);
}
void DFS(int start, int target, std::vector<bool>& visited, std::vector<int>& path) {
visited[start] = true;
path.push_back(start);
if (start == target) {
// 找到目标,打印路径
std::cout << "关系路径: ";
for (int vertex : path) {
std::cout << vertex << " ";
}
std::cout << std::endl;
} else {
for (int neighbor : adj[start]) {
if (!visited[neighbor]) {
DFS(neighbor, target, visited, path);
}
}
}
// 回溯
visited[start] = false;
path.pop_back();
}
private:
int V; // 顶点数
std::vector<std::vector<int>> adj; // 邻接表
};
int main() {
Graph socialNetwork(7); // 创建一个具有7个顶点的社交关系图
// 添加社交关系边
socialNetwork.addEdge(0, 1);
socialNetwork.addEdge(0, 2);
socialNetwork.addEdge(1, 3);
socialNetwork.addEdge(1, 4);
socialNetwork.addEdge(2, 5);
socialNetwork.addEdge(3, 6);
std::vector<bool> visited(7, false);
std::vector<int> path;
std::cout << "查找朋友之间的关系路径:" << std::endl;
socialNetwork.DFS(0, 6, visited, path); // 查找从顶点0到顶点6的关系路径
return 0;
}
运行结果: 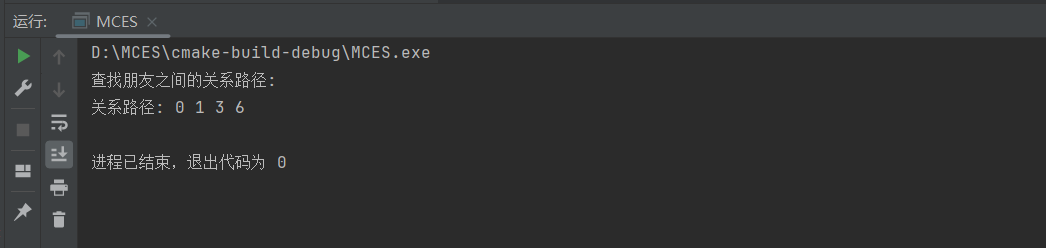
注意:这个示例代码演示了如何创建一个社交关系图,并使用DFS来查找朋友之间的关系路径。实际应用中,社交网络可能包含更多顶点和更复杂的关系。