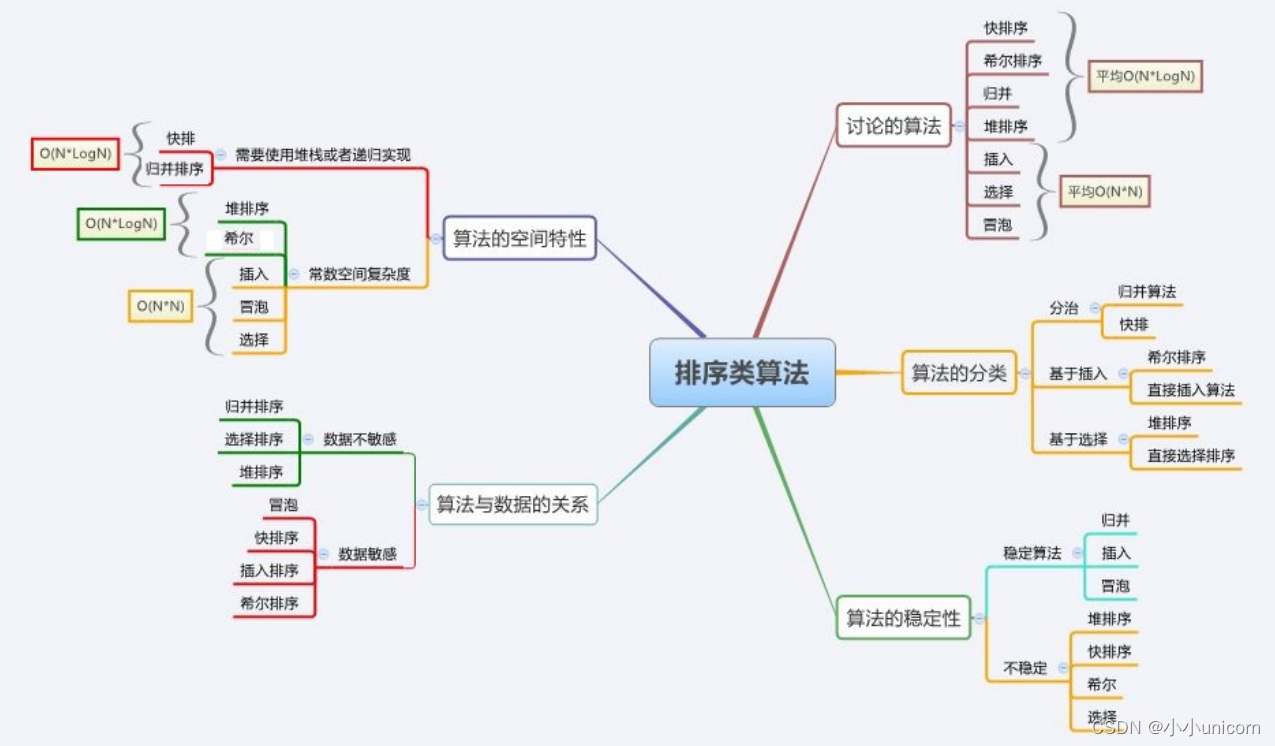
本专栏内容为:八大排序汇总 通过本专栏的深入学习,你可以了解并掌握八大排序以及相关的排序算法。
💓博主csdn个人主页:小小unicorn
⏩专栏分类:八大排序汇总
🚚代码仓库:小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识
目录
- 直接插入排序
- 希尔排序
- 选择排序
- 堆排序
- 冒泡排序
- 快速排序
- 递归实现
- Hoare版本
- 挖坑法
- 前后指针法
- 非递归实现
- 快速排序的两个优化版本
- 三数取中
- 小区间优化
- 归并排序
- 递归实现
- 非递归实现
- 计数排序
- 排序算法复杂度及稳定性分析
直接插入排序
动图演示:
插入排序,又叫直接插入排序。实际中,我们玩扑克牌的时候,就用了插入排序的思想。
基本思想:
在待排序的元素中,假设前n-1个元素已有序,现将第n个元素插入到前面已经排好的序列中,使得前n个元素有序。按照此法对所有元素进行插入,直到整个序列有序。
注意:
我们并不能确定待排元素中究竟哪一部分是有序的,所以我们一开始只能认为第一个元素是有序的,依次将其后面的元素插入到这个有序序列中来,直到整个序列有序为止。
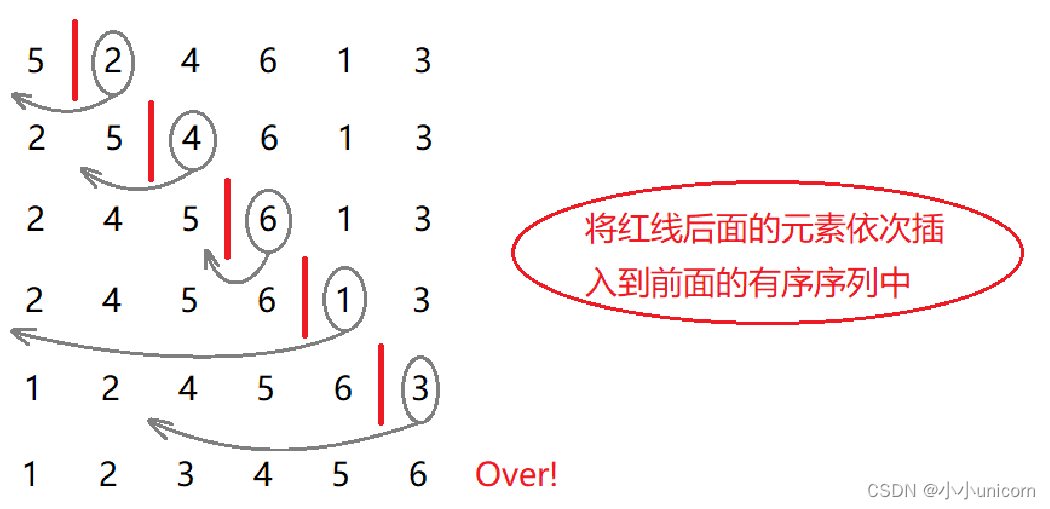
代码实现:
//插入排序
void InsertSort(int* a, int n)
{
int i = 0;
//整体:
for (i = 0; i < n - 1; i++)
{
//单趟:
//[0,end]有序,把end+1的位置的插入到前序序列
//控制[0,end+1]有序
int end = i;
int tmp = a[end + 1];//待插入的元素
while (end >= 0)
{
if (tmp < a[end])//还需继续比较
{
a[end + 1] = a[end];
}
else//找到应插入的位置
{
break;
}
--end;
}
a[end + 1] = tmp;
//代码执行到此位置有两种情况:
//1.待插入元素找到应插入位置(break跳出循环到此)。
//2.待插入元素比当前有序序列中的所有元素都小(while循环结束后到此)。
}
}
1.时间复杂度:O (N2)
2.空间复杂度:O (1)
3.稳定性:稳定
希尔排序
动图演示:
 .希尔排序是按其设计者希尔的名字命名的,该算法由希尔1959年公布。希尔对普通插入排序的时间复杂度进行分析,得出了以下结论:
.希尔排序是按其设计者希尔的名字命名的,该算法由希尔1959年公布。希尔对普通插入排序的时间复杂度进行分析,得出了以下结论:
1.普通插入排序的时间复杂度最坏情况下为O(N2),此时待排序列为逆序,或者说接近逆序。
2.普通插入排序的时间复杂度最好情况下为O(N),此时待排序列为升序,或者说接近升序。

于是希尔就思考:若是能先将待排序列进行一次预排序,使待排序列接近有序(接近我们想要的顺序),然后再对该序列进行一次直接插入排序。因为此时直接插入排序的时间复杂度为O(N),那么只要控制预排序阶段的时间复杂度不超过O(N2),那么整体的时间复杂度就比直接插入排序的时间复杂度低了。
希尔排序,又称缩小增量法。其基本思想是:
1.先选定一个小于N的整数gap作为第一增量,然后将所有距离为gap的元素分在同一组,并对每一组的元素进行直接插入排序。然后再取一个比第一增量小的整数作为第二增量,重复上述操作…
2.当增量的大小减到1时,就相当于整个序列被分到一组,进行一次直接插入排序,排序完成。
思考一下:为什么要让gap由大到小呢?
回答:gap越大,数据挪动得越快;gap越小,数据挪动得越慢。
前期让gap较大,可以让数据更快得移动到自己对应的位置附近,减少挪动次数。
注意:一般情况下,我们取序列的一半作为增量,然后依次减半,直到增量为1(也可自己设置)。
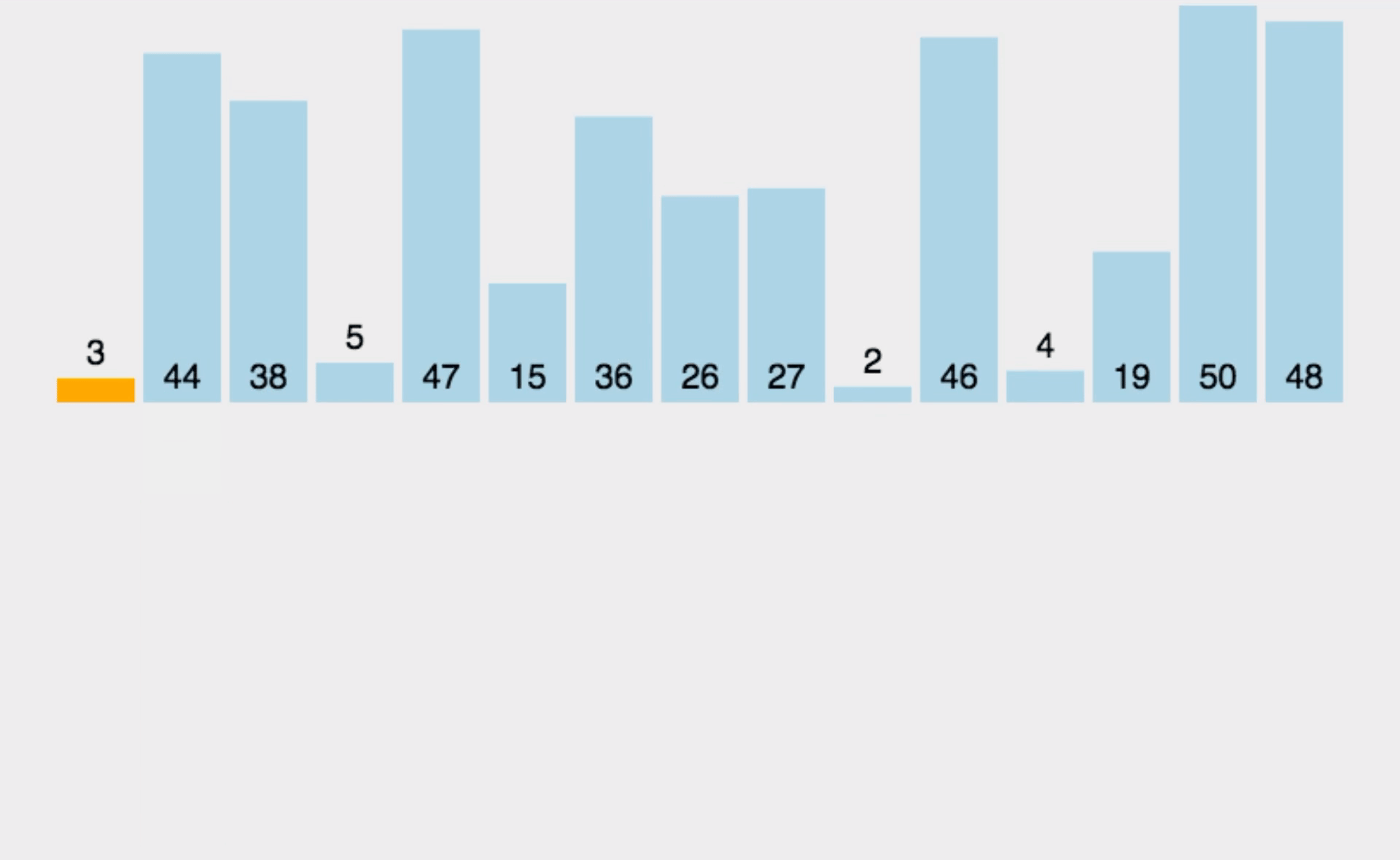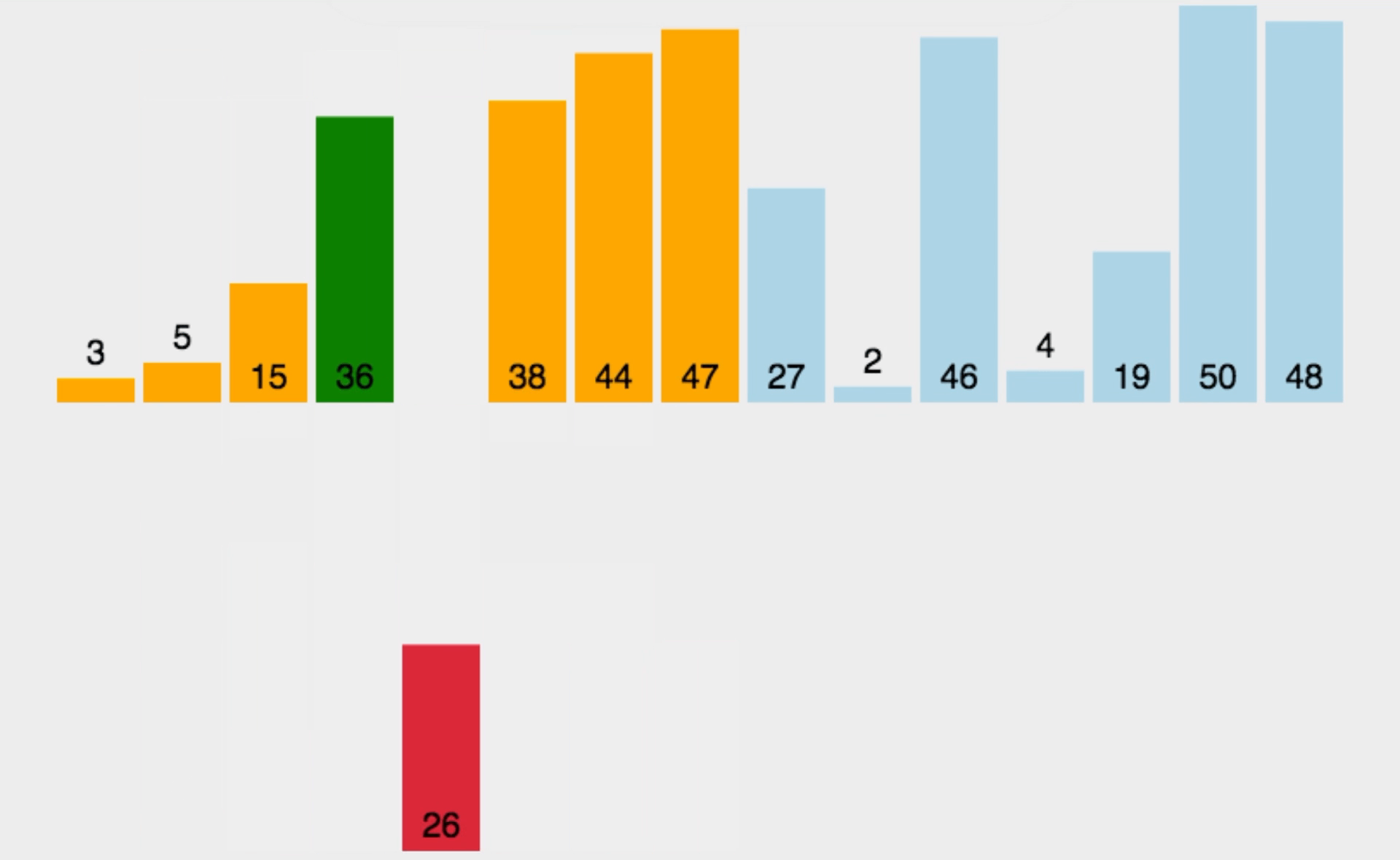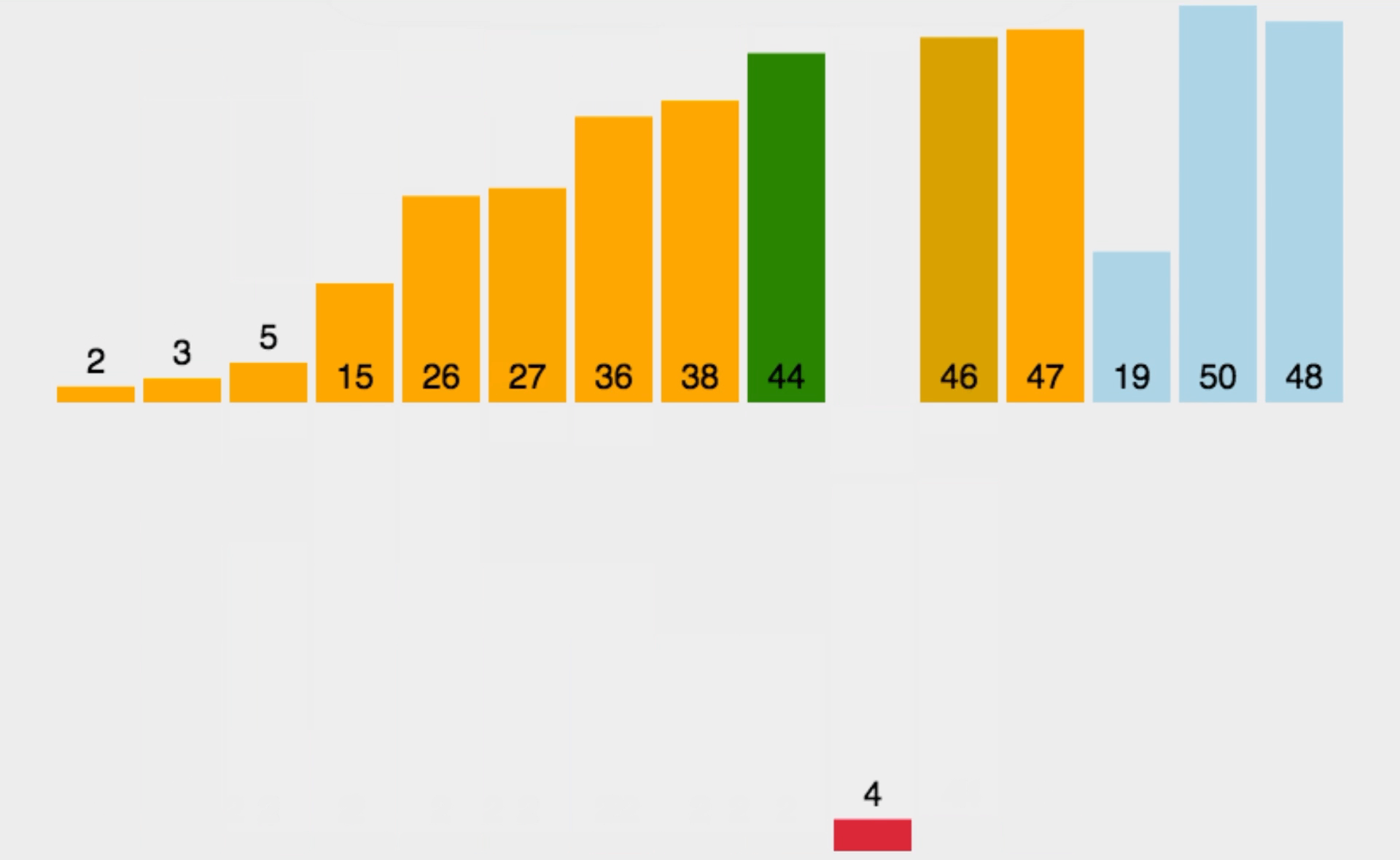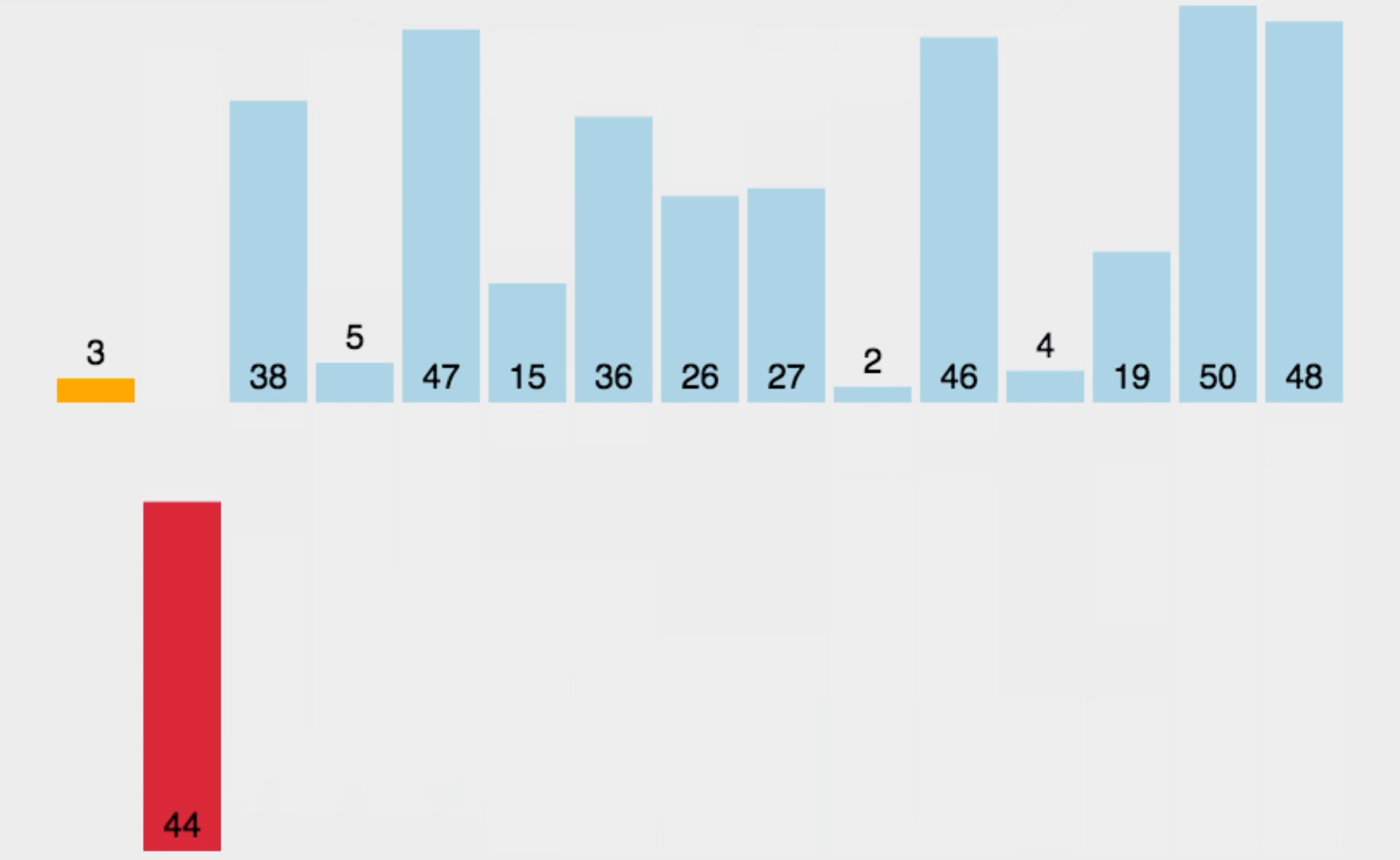
举个例子分析一下:
现在我们用希尔排序对该序列进行排序。

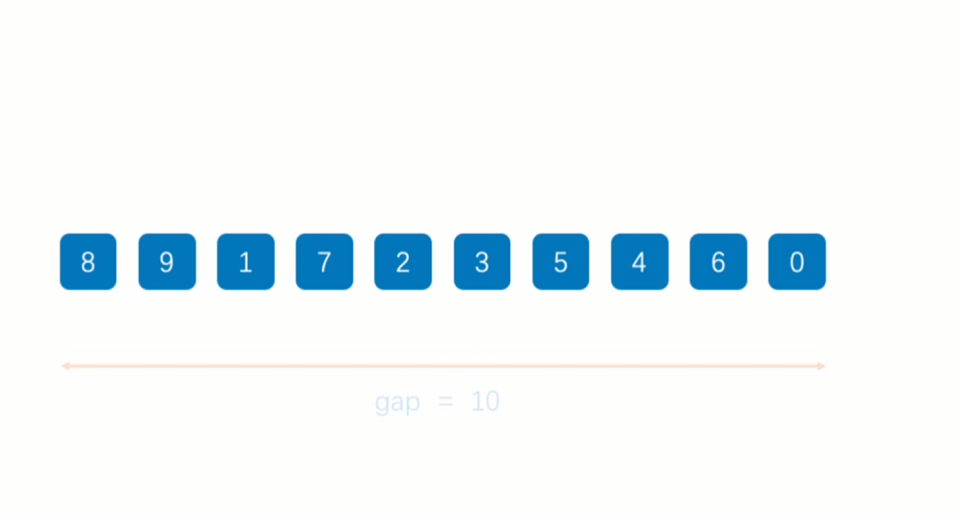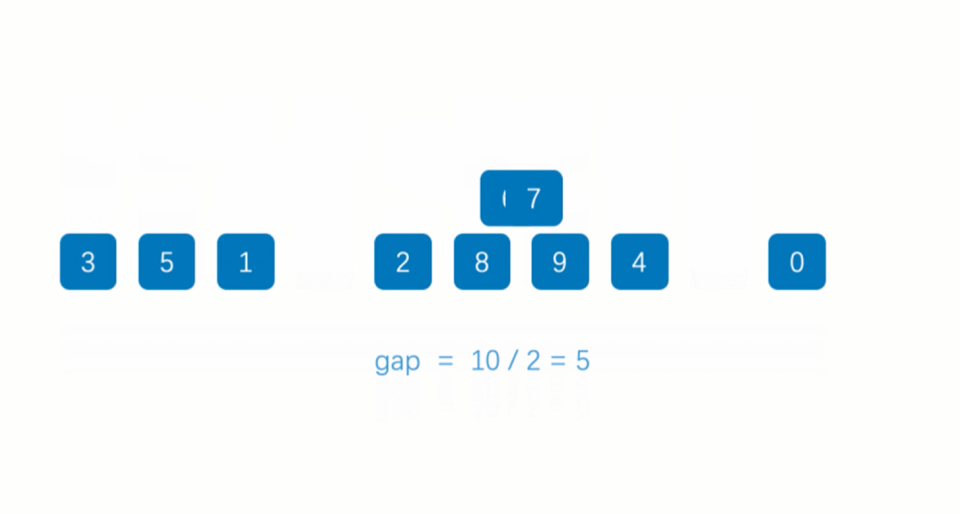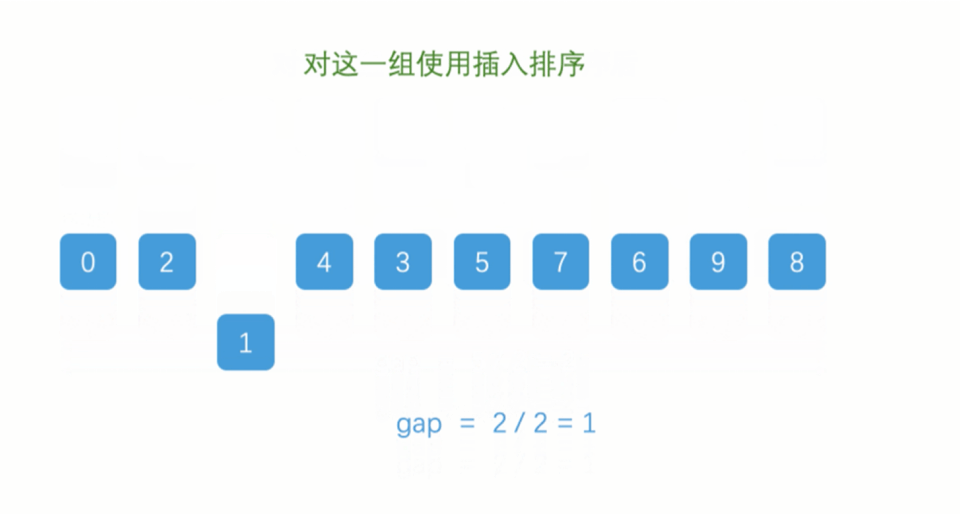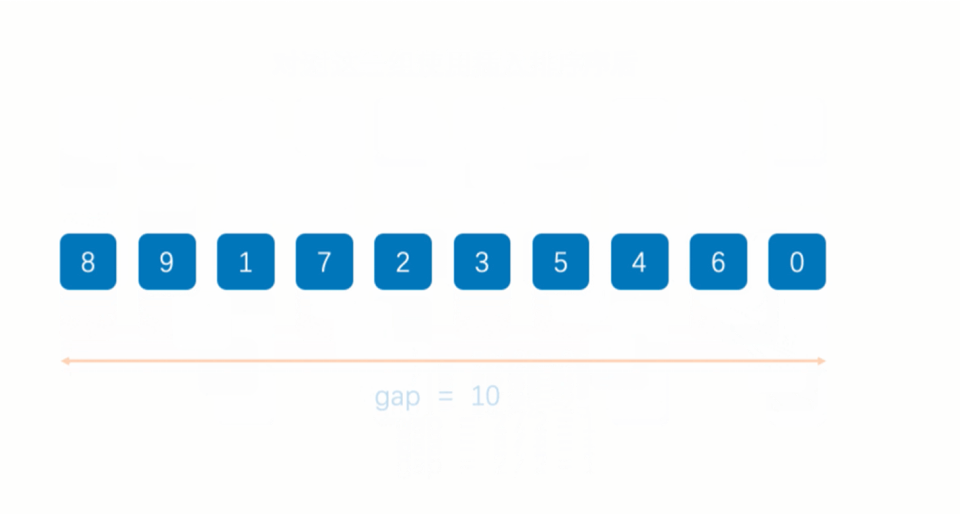
我们用序列长度的一半作为第一次排序时gap的值,此时相隔距离为5的元素被分为一组(共分了5组,每组有2个元素),然后分别对每一组进行直接插入排序。

gap的值折半,此时相隔距离为2的元素被分为一组(共分了2组,每组有5个元素),然后再分别对每一组进行直接插入排序。

gap的值再次折半,此时gap减为1,即整个序列被分为一组,进行一次直接插入排序。

该例子中,前两趟就是希尔排序的预排序,而最后一趟实现的是希尔排序的直接插入排序。
代码实现:
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
//gap = gap / 2;
gap = gap / 3 + 1;
for (int i = 0; i < n - gap; ++i)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些书籍中给出的希尔排序的时间复杂度都不固定。


因为咱们的gap是按照Knuth提出的方式取值的,而且Knuth进行了大量的试验统计,我们暂时就按照:O(N1.25)或者O(1.6*N1.25)来进行计算。
稳定性:不稳定
选择排序
动图演示:
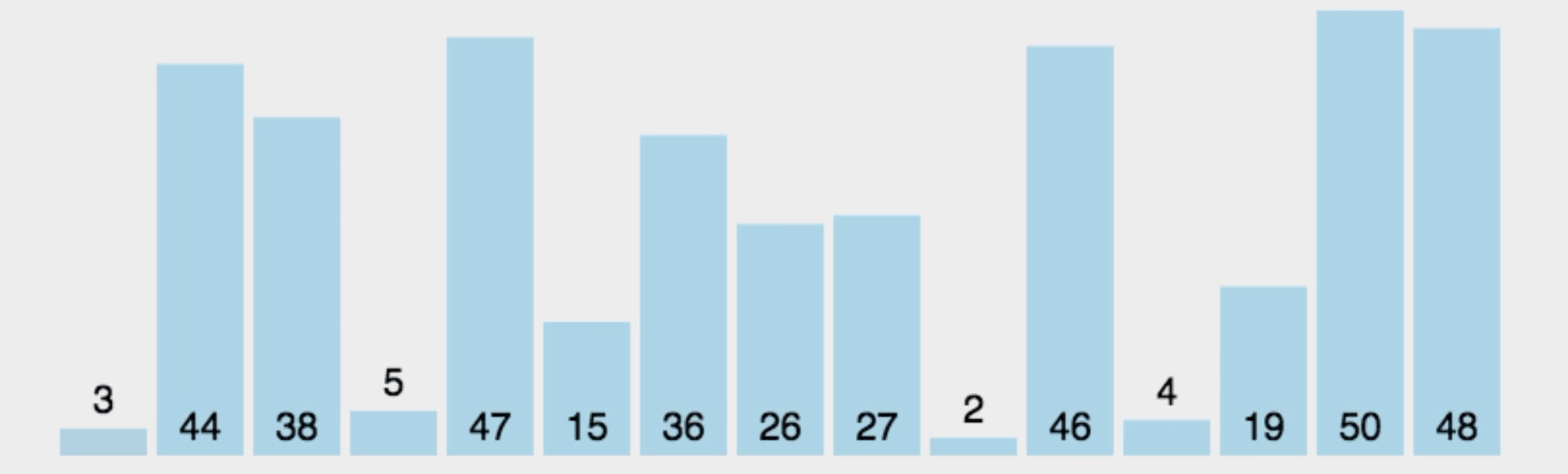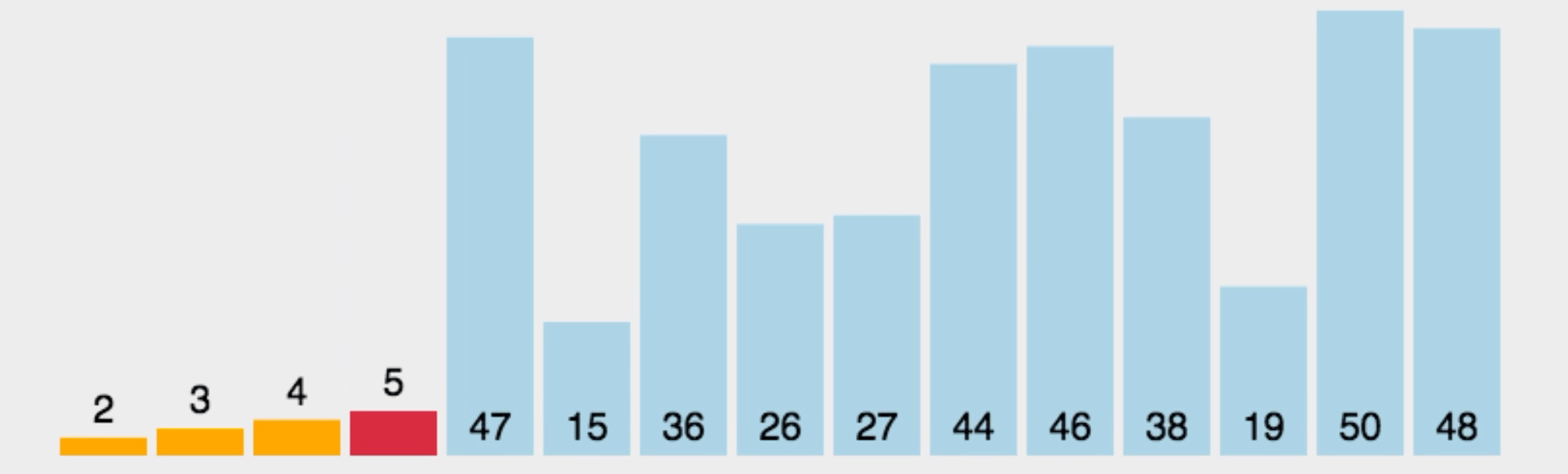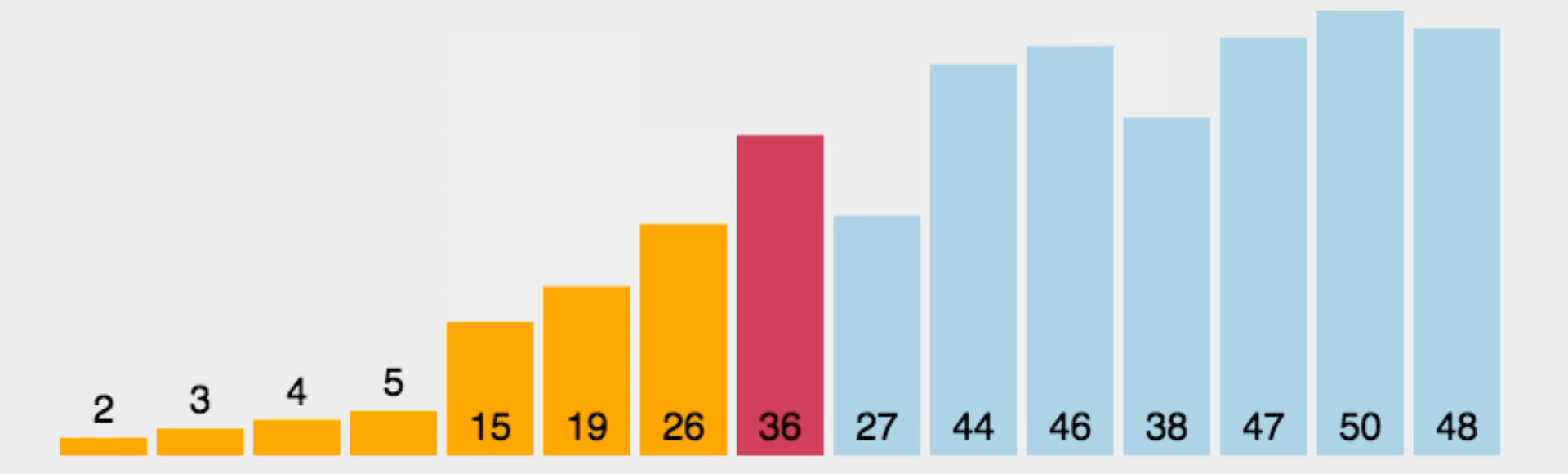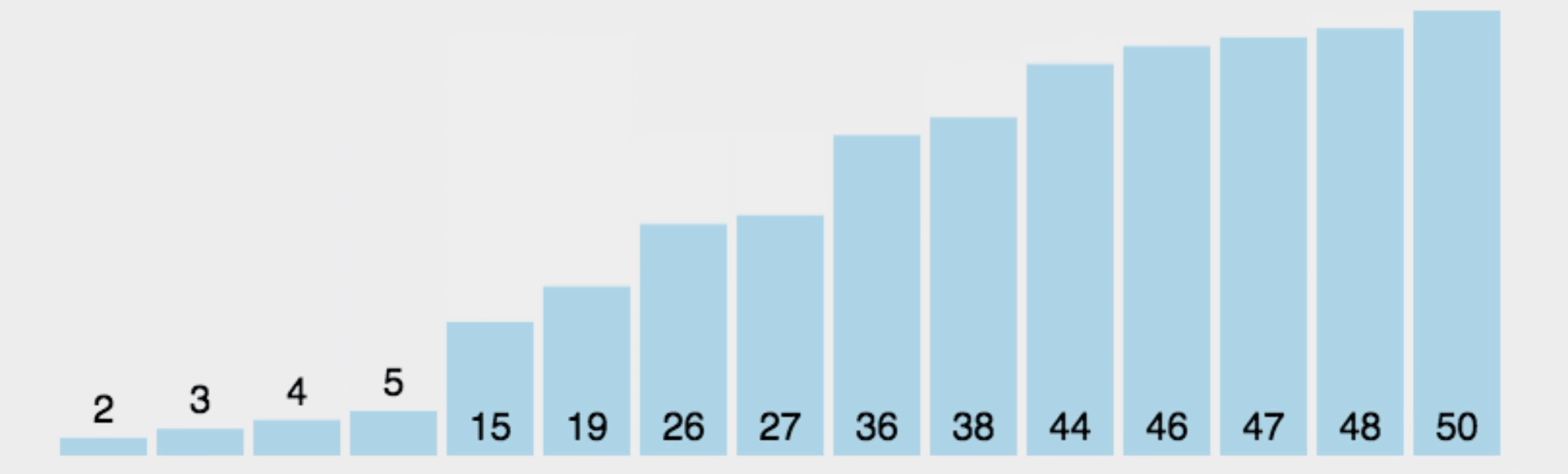
选择排序,即每次从待排序列中选出一个最小值,然后放在序列的起始位置,直到全部待排数据排完即可。
//选择排序(一次选一个数)
void SelectSort(int* a, int n)
{
int i = 0;
for (i = 0; i < n; i++)//i代表参与该趟选择排序的第一个元素的下标
{
int start = i;
int min = start;//记录最小元素的下标
while (start < n)
{
if (a[start] < a[min])
min = start;//最小值的下标更新
start++;
}
Swap(&a[i], &a[min]);//最小值与参与该趟选择排序的第一个元素交换位置
}
}
我们可以一趟选出两个值,一个最大值一个最小值,然后将其放在序列开头和末尾,这样可以使选择排序的效率快一倍。
代码实现:
//选择排序(一次选两个数)
void SelectSort(int* a, int n)
{
int left = 0;//记录参与该趟选择排序的第一个元素的下标
int right = n - 1;//记录参与该趟选择排序的最后一个元素的下标
while (left < right)
{
int minIndex = left;//记录最小元素的下标
int maxIndex = left;//记录最大元素的下标
int i = 0;
//找出最大值及最小值的下标
for (i = left; i <= right; i++)
{
if (a[i] < a[minIndex])
minIndex = i;
if (a[i] > a[maxIndex])
maxIndex = i;
}
//将最大值和最小值放在序列开头和末尾
Swap(&a[minIndex], &a[left]);
if (left == maxIndex)
{
maxIndex = minIndex;//防止最大值位于序列开头,被最小值交换
}
Swap(&a[maxIndex], &a[right]);
left++;
right--;
}
}
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
堆排序
动图演示:

在之前的文章:堆的介绍中,我们知道堆的介绍,如何建堆,以及堆的向上,向下调整法的实现,而堆排序就是依靠建堆,通过堆的方式的进行排序。至于堆的建立与实现,本文章就不过多叙述了,详情请点击堆的介绍与实现查看。
堆建好后,如何进行堆排序,步骤如下:
1、将堆顶数据与堆的最后一个数据交换,然后对根位置进行一次堆的向下调整,但是调整时被交换到最后的那个最大的数不参与向下调整。
2、完成步骤1后,这棵树除最后一个数之外,其余数又成一个大堆,然后又将堆顶数据与堆的最后一个数据交换,这样一来,第二大的数就被放到了倒数第二个位置上,然后该数又不参与堆的向下调整…反复执行下去,直到堆中只有一个数据时便结束。此时该序列就是一个升序。
代码实现:
//向下调整法:
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
// 找出小的那个孩子
if (child + 1 < n && a[child + 1] > a[child])
{
++child;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
// 继续往下调整
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
/堆排序
void HeapSort(int* a, int n)
{
// 向下调整建堆
// O(N)
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
// O(N*logN)
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
冒泡排序
动图演示:
冒泡排序(Bubble Sort):是一种交换排序,它的基本思想是:两两比较相邻记录的关键字,如果反序则交换,直到没有反序的记录为止。
void BubbleSort(int* a, int n)
{
for (size_t j = 0; j < n; j++)
{
int exchange = 0;
for (size_t i = 1; i < n - j; i++)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
{
break;
}
}
}
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
快速排序
递归实现
Hoare版本
动图演示:
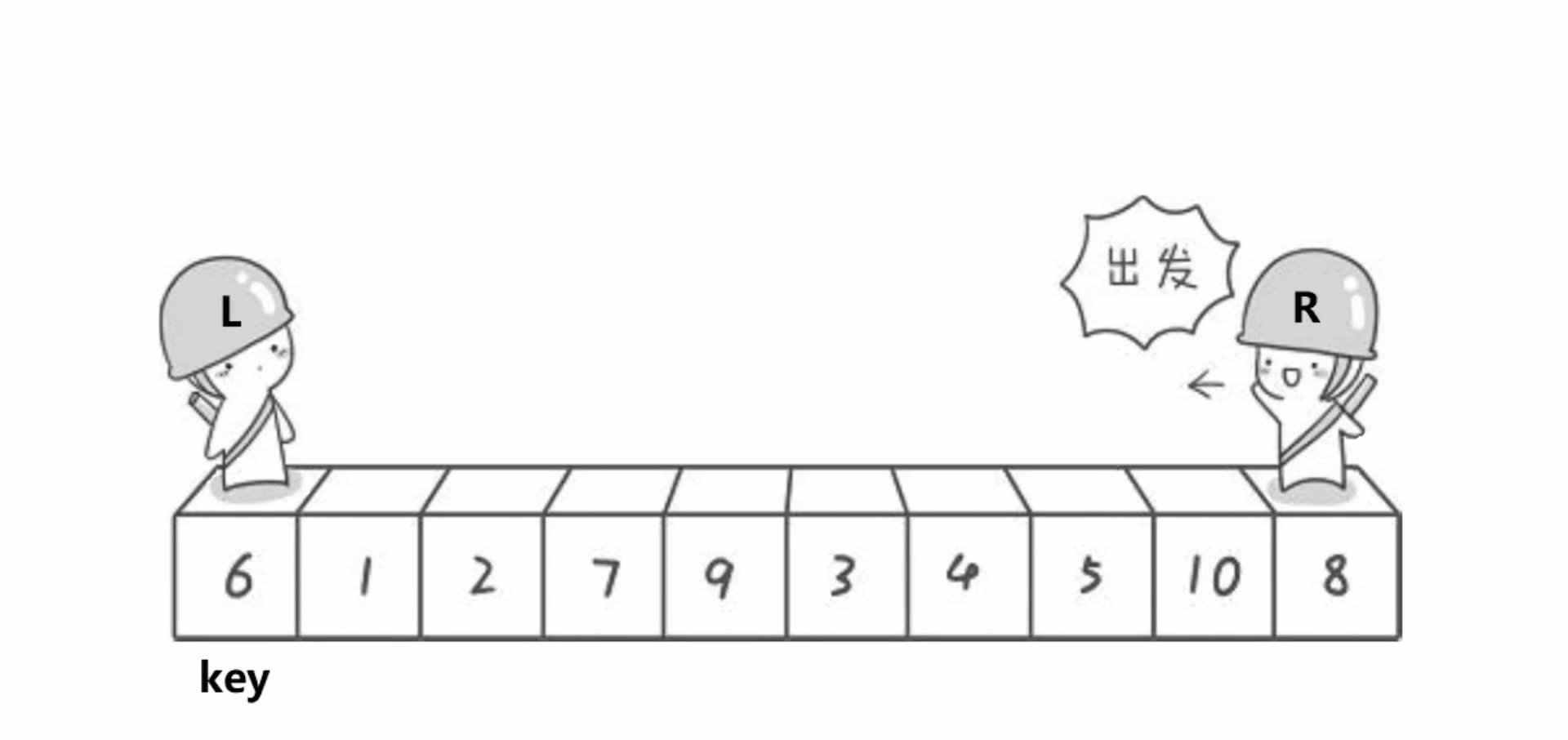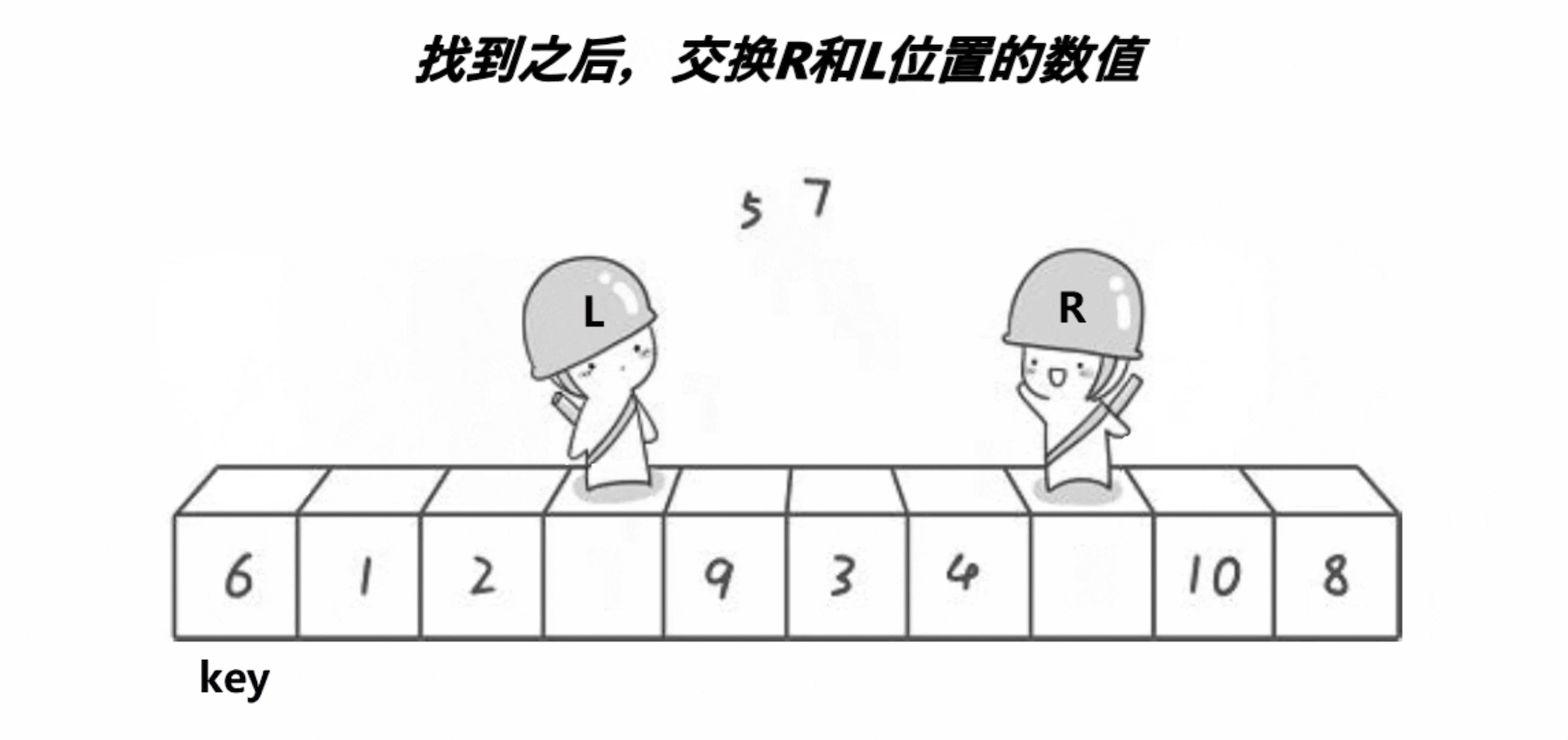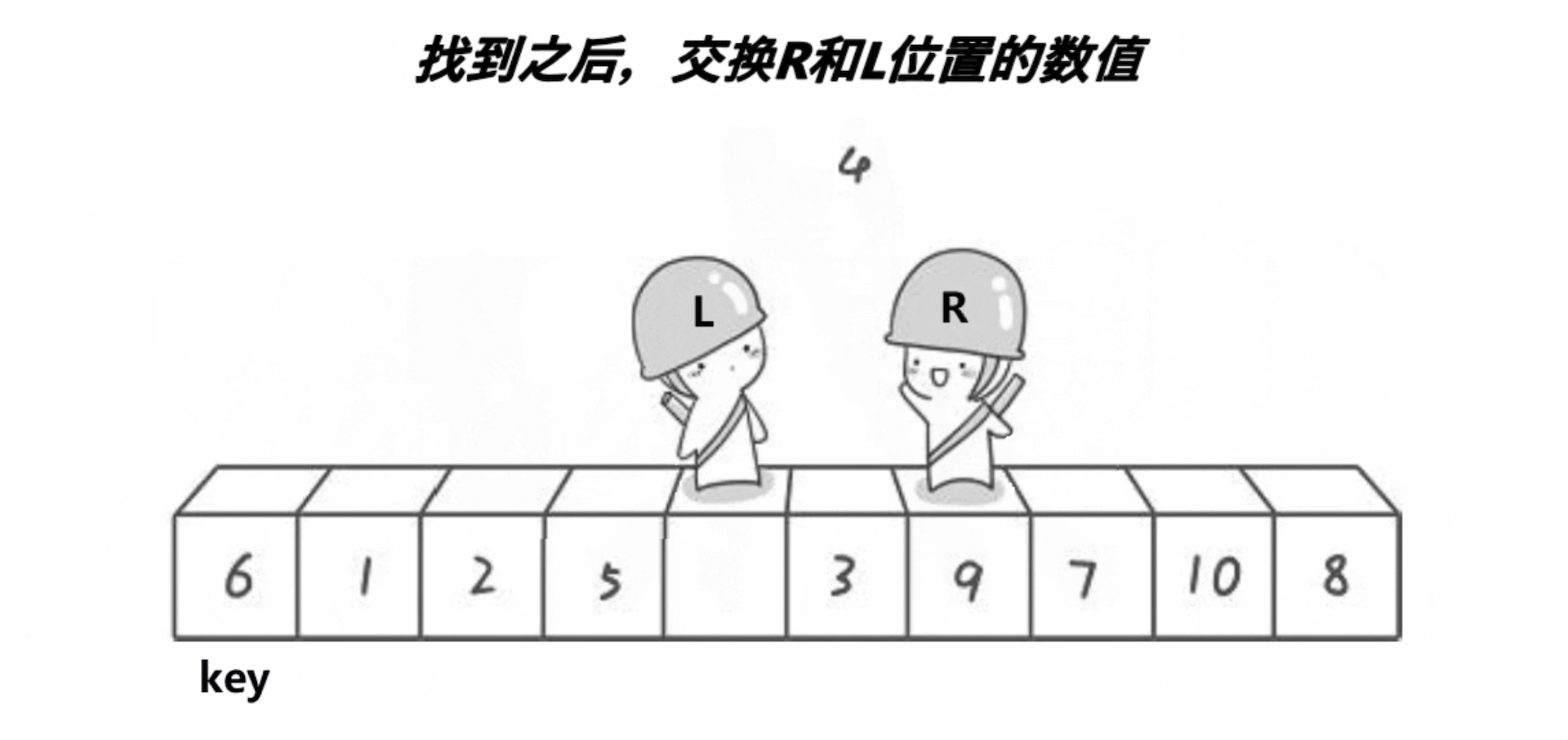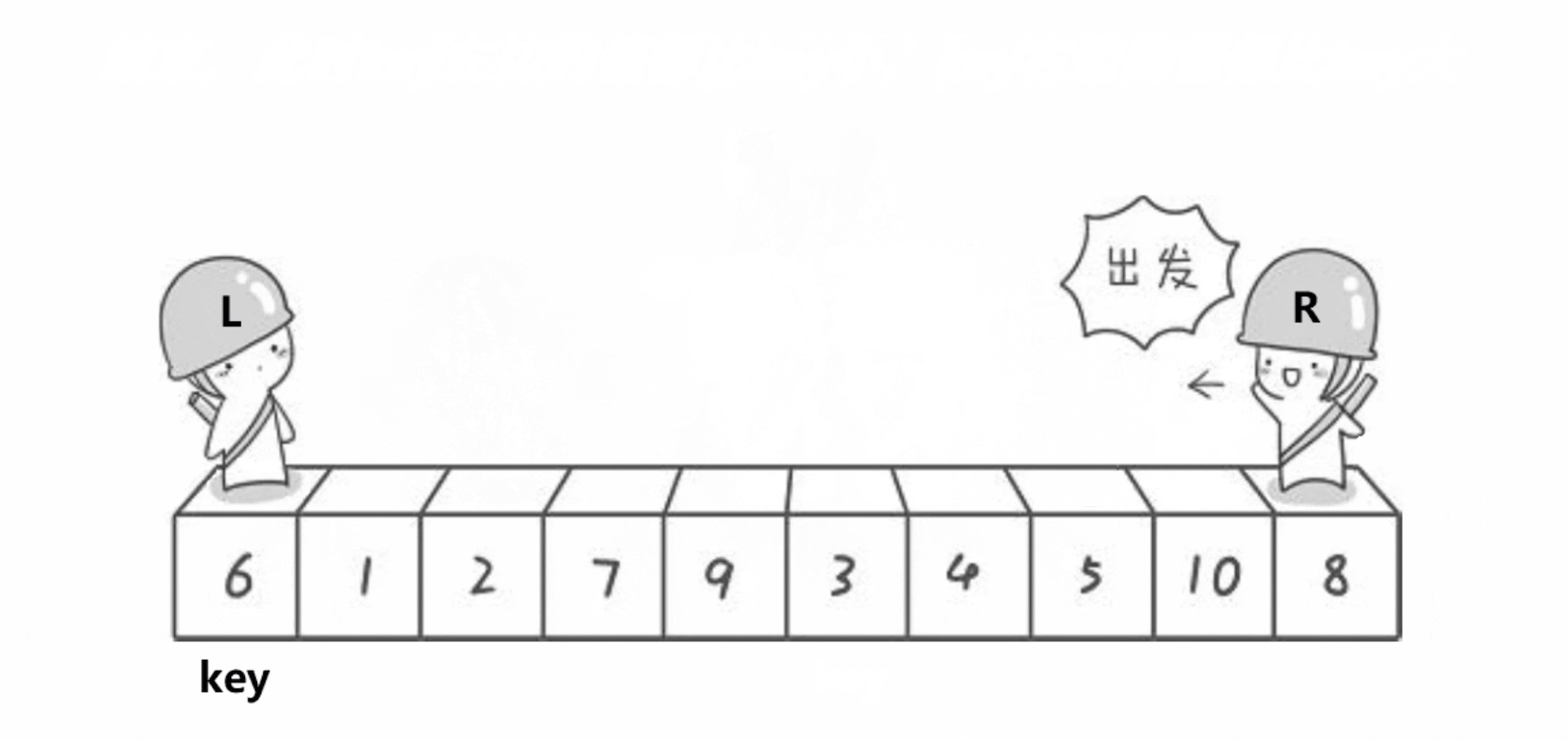
Hoare版本的单趟排序的基本步骤如下:
1、选出一个key,一般是最左边或是最右边的。
2、定义一个L和一个R,L从左向右走,R从右向左走。(需要注意的是:若选择最左边的数据作为key,则需要R先走;若选择最右边的数据作为key,则需要L先走)。
3、在走的过程中,若R遇到小于key的数,则停下,L开始走,直到L遇到一个大于key的数时,将L和R的内容交换,R再次开始走,如此进行下去,直到L和R最终相遇,此时将相遇点的内容与key交换即可。(选取最左边的值作为key)
经过一次单趟排序,最终使得key左边的数据全部都小于key,key右边的数据全部都大于key。
然后我们在将key的左序列和右序列再次进行这种单趟排序,如此反复操作下去,直到左右序列只有一个数据,或是左右序列不存在时,便停止操作,因为这种序列可以认为是有序的。
单趟排序代码实现:
// Hoare版本
int PartSort1(int* a, int left, int right)
{
//三数取中
/*int midi = GetMidi(a, left, right);
Swap(&a[left], &a[midi]);*/
int keyi = left;
while (left < right)
{
// 找小
while (left < right && a[right] >= a[keyi])
{
--right;
}
// 找大
while (left < right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[left], &a[right]);
}
Swap(&a[keyi], &a[left]);
return left;
}
整体递归实现:
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
return;
int keyi = PartSort1(a, begin, end);
// [begin, keyi-1] keyi [keyi+1, end]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
挖坑法
动图演示:
挖坑法的单趟排序的基本步骤如下:
1、选出一个数据(一般是最左边或是最右边的)存放在key变量中,在该数据位置形成一个坑。
2、还是定义一个L和一个R,L从左向右走,R从右向左走。(若在最左边挖坑,则需要R先走;若在最右边挖坑,则需要L先走)。
3、在走的过程中,若R遇到小于key的数,则将该数抛入坑位,并在此处形成一个坑位,这时L再向后走,若遇到大于key的数,则将其抛入坑位,又形成一个坑位,如此循环下去,直到最终L和R相遇,这时将key抛入坑位即可。(选取最左边的作为坑位)
经过一次单趟排序,最终也使得key左边的数据全部都小于key,key右边的数据全部都大于key。
然后也是将key的左序列和右序列再次进行这种单趟排序,如此反复操作下去,直到左右序列只有一个数据,或是左右序列不存在时,便停止操作。
单趟排序代码实现:
// 挖坑法
int PartSort2(int* a, int left, int right)
{
//三数取中优化
/*int midi = GetMidi(a, left, right);
Swap(&a[left], &a[midi]);*/
int key = a[left];
// 保存key值以后,左边形成第一个坑
int hole = left;
while (left < right)
{
// 右边先走,找小,填到左边的坑,右边形成新的坑位
while (left < right && a[right] >= key)
{
--right;
}
a[hole] = a[right];
hole = right;
// 左边再走,找大,填到右边的坑,左边形成新的坑位
while (left < right && a[left] <= key)
{
++left;
}
a[hole] = a[left];
hole = left;
}
a[hole] = key;
return hole;
}
整体递归实现:
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
return;
int keyi = PartSort2(a, begin, end);
// [begin, keyi-1] keyi [keyi+1, end]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
前后指针法
动图演示:
前后指针法的单趟排序的基本步骤如下:
1、选出一个key,一般是最左边或是最右边的。
2、起始时,prev指针指向序列开头,cur指针指向prev+1。
3、若cur指向的内容小于key,则prev先向后移动一位,然后交换prev和cur指针指向的内容,然后cur指针++;若cur指向的内容大于key,则cur指针直接++。如此进行下去,直到cur指针越界,此时将key和prev指针指向的内容交换即可。
经过一次单趟排序,最终也能使得key左边的数据全部都小于key,key右边的数据全部都大于key。
然后也还是将key的左序列和右序列再次进行这种单趟排序,如此反复操作下去,直到左右序列只有一个数据,或是左右序列不存在时,便停止操作。
单趟排序代码实现:
// 前后指针
int PartSort3(int* a, int left, int right)
{
//三数取中
/*int midi = GetMidi(a, left, right);
Swap(&a[left], &a[midi]);*/
int prev = left;
int cur = prev + 1;
int keyi = left;
while (cur <= right)
{
if (a[cur] < a[keyi] && ++prev != cur)
{
Swap(&a[prev], &a[cur]);
}
++cur;
}
Swap(&a[prev], &a[keyi]);
return prev;
}
整体递归实现:
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
return;
int keyi = PartSort3(a, begin, end);
// [begin, keyi-1] keyi [keyi+1, end]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
- 时间复杂度:O(N*logN)
- 空间复杂度:O(logN)
- 稳定性:不稳定
非递归实现
快速排序的非递归算法基本思路:
1、先将待排序列的第一个元素的下标和最后一个元素的下标入栈。
2、当栈不为空时,读取栈中的信息(一次读取两个:一个是L,另一个是R),然后调用某一版本的单趟排序,排完后获得了key的下标,然后判断key的左序列和右序列是否还需要排序,若还需要排序,就将相应序列的L和R入栈;若不需排序了(序列只有一个元素或是不存在),就不需要将该序列的信息入栈。
3、反复执行步骤2,直到栈为空为止。
在实现快排的非递归时,需要用到栈,所以,我们首先要进行栈的实现,代码如下:
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
//#define N 10
//struct Stack
//{
// int a[N];
// int top;
//};
typedef int STDataType;
typedef struct Stack
{
STDataType* a;
int top;
int capacity;
}ST;
void STInit(ST* ps)
{
assert(ps);
ps->a = NULL;
ps->capacity = 0;
ps->top = 0;
}
void STDestroy(ST* ps)
{
assert(ps);
free(ps->a);
ps->a = NULL;
ps->top = ps->capacity = 0;
}
void STPush(ST* ps, STDataType x)
{
assert(ps);
// 11:40
if (ps->top == ps->capacity)
{
int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newCapacity);
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
ps->a = tmp;
ps->capacity = newCapacity;
}
ps->a[ps->top] = x;
ps->top++;
}
void STPop(ST* ps)
{
assert(ps);
//
assert(ps->top > 0);
--ps->top;
}
STDataType STTop(ST* ps)
{
assert(ps);
//
assert(ps->top > 0);
return ps->a[ps->top - 1];
}
int STSize(ST* ps)
{
assert(ps);
return ps->top;
}
bool STEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;
}
要是对栈的基本操作实现还有问题的,可以查看小编的文章:栈的介绍与实现
非递归快排完整代码如下:
//快排非递归实现:
void QuickSortNonR(int* a, int begin, int end)
{
ST st;
STInit(&st);
STPush(&st, end);
STPush(&st, begin);
while (!STEmpty(&st))
{
int left = STTop(&st);
STPop(&st);
int right = STTop(&st);
STPop(&st);
int keyi = PartSort1(a, left, right);
// [lefy,keyi-1] keyi [keyi+1, right]
if (keyi + 1 < right)
{
STPush(&st, right);
STPush(&st, keyi + 1);
}
if (left < keyi - 1)
{
STPush(&st, keyi - 1);
STPush(&st, left);
}
}
STDestroy(&st);
}
快速排序的两个优化版本
三数取中
快速排序的时间复杂度是O(NlogN),是我们在理想情况下计算的结果。在理想情况下,我们每次进行完单趟排序后,key的左序列与右序列的长度都相同:
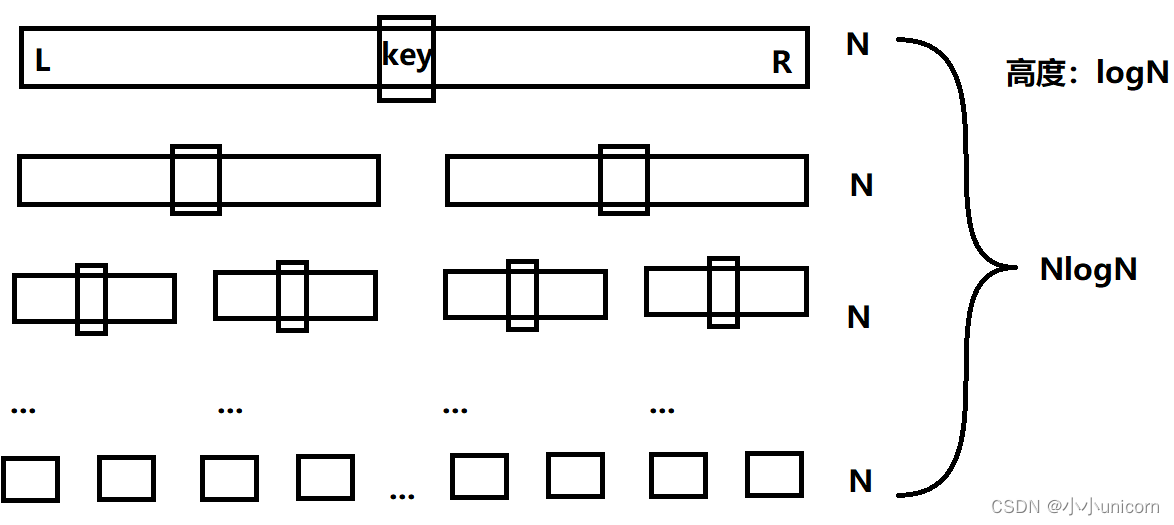
若每趟排序所选的key都正好是该序列的中间值,即单趟排序结束后key位于序列正中间,那么快速排序的时间复杂度就是O(NlogN)。
可是谁也不能保证每次选取的key都是正中间的那个数,当待排序列本就是一个有序的序列时,我们若是依然每次都选取最左边或是最右边的数作为key,那么快速排序的效率将达到最低:
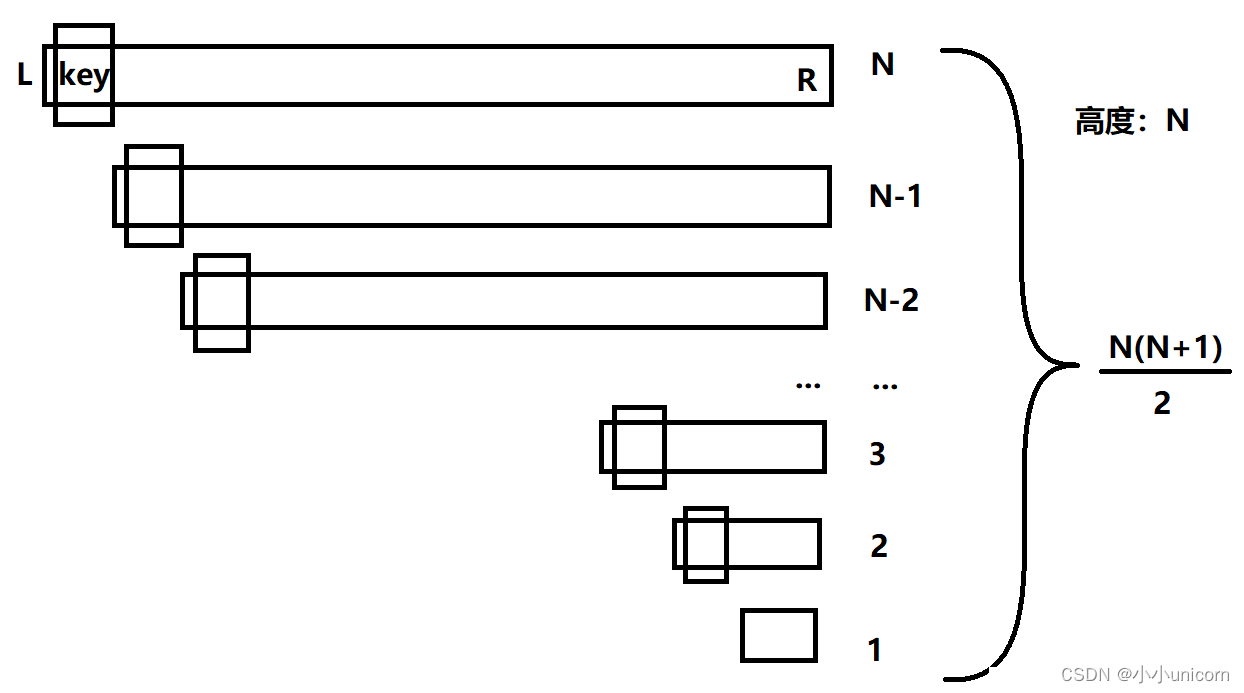
可以看到,这种情况下,快速排序的时间复杂度退化为O(N2)。其实,对快速排序效率影响最大的就是选取的key,若选取的key越接近中间位置,则则效率越高。
为了避免这种极端情况的发生,于是出现了三数取中:
三数取中,当中的三数指的是:最左边的数、最右边的数以及中间位置的数。三数取中就是取这三个数当中,值的大小居中的那个数作为该趟排序的key。这就确保了我们所选取的数不会是序列中的最大或是最小值了。
// 三数取中
int GetMidi(int* a, int left, int right)
{
int mid = (left + right) / 2;
// left mid right
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] > a[right]) // mid是最大值
{
return left;
}
else
{
return right;
}
}
else // a[left] > a[mid]
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] < a[right]) // mid是最小
{
return left;
}
else
{
return right;
}
}
}
注意:当大小居中的数不在序列的最左或是最右端时,我们不是就以居中数的位置作为key的位置,而是将key的值与最左端的值进行交换,这样key就还是位于最左端了,所写代码就无需改变,而只需在单趟排序代码开头加上以下两句代码即可:
int midIndex = GetMidIndex(a, begin, end);//获取大小居中的数的下标
Swap(&a[begin], &a[midIndex]);//将该数与序列最左端的数据交换
//以下代码保持不变...
小区间优化
我们可以看到,就算是上面理想状态下的快速排序,也不能避免随着递归的深入,每一层的递归次数会以2倍的形式快速增长。
为了减少递归树的最后几层递归,我们可以设置一个判断语句,当序列的长度小于某个数的时候就不再进行快速排序,转而使用其他种类的排序。小区间优化若是使用得当的话,会在一定程度上加快快速排序的效率,而且待排序列的长度越长,该效果越明显。
代码实现:
//小区间优化
void QuickSort1(int* a, int begin, int end)
{
if (begin >= end)
return;
// 小区间优化,小区间不再递归分割排序,降低递归次数
if ((end - begin + 1) > 10)//可以自行微调
{
//可调用快速排序的单趟排序三种中的任意一种
//int keyi = PartSort1(a, begin, end);
//int keyi = PartSort2(a, begin, end);
int keyi = PartSort3(a, begin, end);
// [begin, keyi-1] keyi [keyi+1, end]
QuickSort1(a, begin, keyi - 1);
QuickSort1(a, keyi + 1, end);
}
else
{
InsertSort(a + begin, end - begin + 1);
}
}
归并排序
动图演示:

归并排序是采用分治法的一个非常典型的应用。其基本思想是:将已有序的子序合并,从而得到完全有序的序列,即先使每个子序有序,再使子序列段间有序。
那么如何得到有序的子序列呢?当序列分解到只有一个元素或是没有元素时,就可以认为是有序了,这时分解就结束了,开始合并:
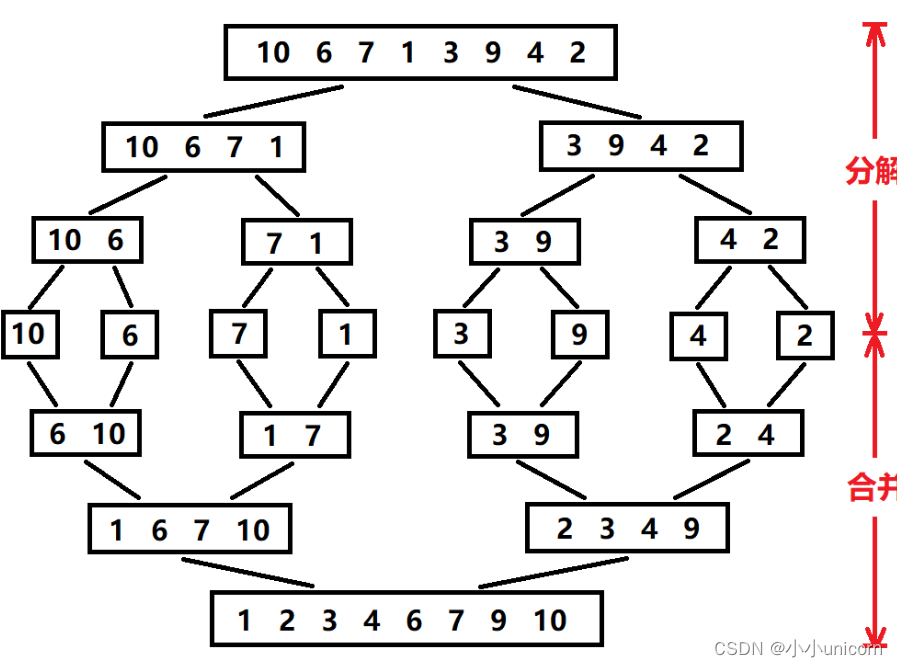
递归实现
//归并排序(子函数)
void _MergeSort(int* a, int left, int right, int* tmp)
{
if (left >= right)//归并结束条件:当只有一个数据或是序列不存在时,不需要再分解
{
return;
}
int mid = left + (right - left) / 2;//中间下标
_MergeSort(a, left, mid, tmp);//对左序列进行归并
_MergeSort(a, mid + 1, right, tmp);//对右序列进行归并
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
//将两段子区间进行归并,归并结果放在tmp中
int i = left;
while (begin1 <= end1&&begin2 <= end2)
{
//将较小的数据优先放入tmp
if (a[begin1] < a[begin2])
tmp[i++] = a[begin1++];
else
tmp[i++] = a[begin2++];
}
//当遍历完其中一个区间,将另一个区间剩余的数据直接放到tmp的后面
while (begin1 <= end1)
tmp[i++] = a[begin1++];
while (begin2 <= end2)
tmp[i++] = a[begin2++];
//归并完后,拷贝回原数组
int j = 0;
for (j = left; j <= right; j++)
a[j] = tmp[j];
}
//归并排序(主体函数)
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int)*n);//申请一个与原数组大小相同的空间
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
_MergeSort(a, 0, n - 1, tmp);//归并排序
free(tmp);//释放空间
}
非递归实现
非递归算法并不需要借助栈来完成,我们只需要控制每次参与合并的元素个数即可,最终便能使序列变为有序:
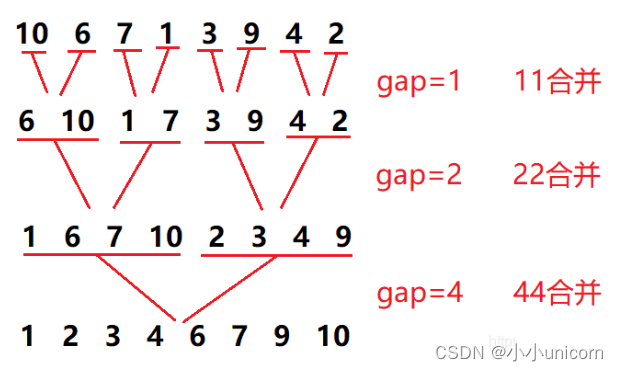
当然,以上例子是一个待排序列长度比较特殊的例子,我们若是想写出一个广泛适用的程序,必定需要考虑到某些极端情况:
情况一:
当最后一个小组进行合并时,第二个小区间存在,但是该区间元素个数不够gap个,这时我们需要在合并序列时,对第二个小区间的边界进行控制。
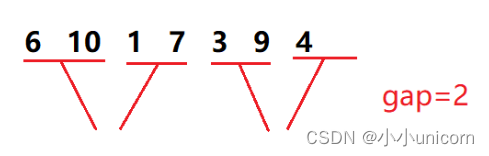
情况二:
当最后一个小组进行合并时,第二个小区间不存在,此时便不需要对该小组进行合并。
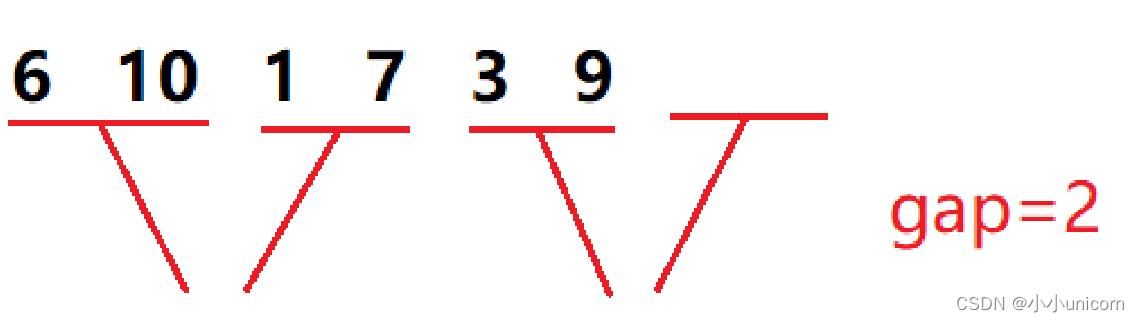
情况三:
当最后一个小组进行合并时,第二个小区间不存在,并且第一个小区间的元素个数不够gap个,此时也不需要对该小组进行合并。(可与情况二归为一类)
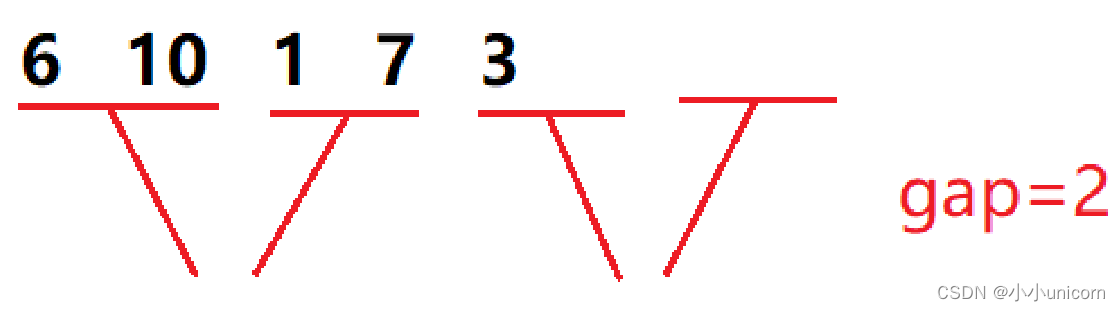
//归并排序(子函数)
void _MergeSortNonR(int* a, int* tmp, int begin1, int end1, int begin2, int end2)
{
int j = begin1;
//将两段子区间进行归并,归并结果放在tmp中
int i = begin1;
while (begin1 <= end1&&begin2 <= end2)
{
//将较小的数据优先放入tmp
if (a[begin1] < a[begin2])
tmp[i++] = a[begin1++];
else
tmp[i++] = a[begin2++];
}
//当遍历完其中一个区间,将另一个区间剩余的数据直接放到tmp的后面
while (begin1 <= end1)
tmp[i++] = a[begin1++];
while (begin2 <= end2)
tmp[i++] = a[begin2++];
//归并完后,拷贝回原数组
for (; j <= end2; j++)
a[j] = tmp[j];
}
//归并排序(主体函数)
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int)*n);//申请一个与待排序列大小相同的空间,用于辅助合并序列
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
int gap = 1;//需合并的子序列中元素的个数
while (gap < n)
{
int i = 0;
for (i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
if (begin2 >= n)//最后一组的第二个小区间不存在或是第一个小区间不够gap个,此时不需要对该小组进行合并
break;
if (end2 >= n)//最后一组的第二个小区间不够gap个,则第二个小区间的后界变为数组的后界
end2 = n - 1;
_MergeSortNonR(a, tmp, begin1, end1, begin2, end2);//合并两个有序序列
}
gap = 2 * gap;//下一趟需合并的子序列中元素的个数翻倍
}
free(tmp);//释放空间
}
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
计数排序
计数排序,又叫非比较排序。顾名思义,该算法不是通过比较数据的大小来进行排序的,而是通过统计数组中相同元素出现的次数,然后通过统计的结果将序列回收到原来的序列中。
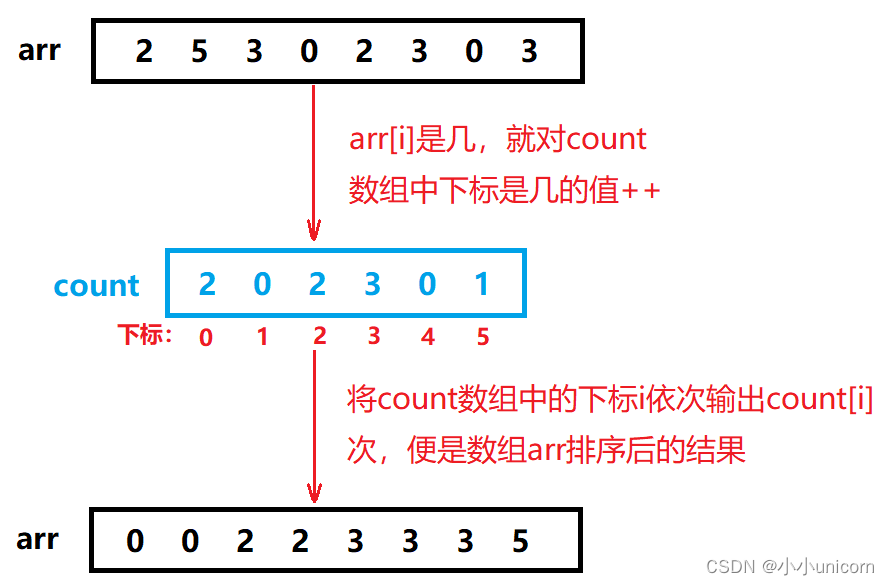
上列中的映射方法称为绝对映射,即arr数组中的元素是几就在count数组中下标为几的位置++,但这样会造成空间浪费。例如,我们要将数组:1020,1021,1018,进行排序,难道我们要开辟1022个整型空间吗?
若是使用计数排序,我们应该使用相对映射,简单来说,数组中的最小值就相对于count数组中的0下标,数组中的最大值就相对于count数组中的最后一个下标。这样,对于数组:1020,1021,1018,我们就只需要开辟用于储存4个整型的空间大小了,此时count数组中下标为i的位置记录的实际上是1018+i这个数出现的次数。
总结:
绝对映射:count数组中下标为i的位置记录的是arr数组中数字i出现的次数。
相对映射:count数组中下标为i的位置记录的是arr数组中数字min+i出现的次数。
注意:计数排序只适用于数据范围较集中的序列的排序,若待排序列的数据较分散,则会造成空间浪费,并且计数排序只适用于整型排序,不适用与浮点型排序。
代码如下:
//计数排序
void CountSort(int* a, int n)
{
int min = a[0];//记录数组中的最小值
int max = a[0];//记录数组中的最大值
for (int i = 0; i < n; i++)
{
if (a[i] < min)
min = a[i];
if (a[i] > max)
max = a[i];
}
int range = max - min + 1;//min和max之间的自然数个数(包括min和max本身)
int* count = (int*)calloc(range, sizeof(int));//开辟可储存range个整型的内存空间,并将内存空间置0
if (count == NULL)
{
printf("malloc fail\n");
exit(-1);
}
//统计相同元素出现次数(相对映射)
for (int i = 0; i < n; i++)
{
count[a[i] - min]++;
}
int i = 0;
//根据统计结果将序列回收到原来的序列中
for (int j = 0; j < range; j++)
{
while (count[j]--)
{
a[i++] = j + min;
}
}
free(count);//释放空间
}
- 时间复杂度:O(MAX(N,range))
- 空间复杂度:O(range)
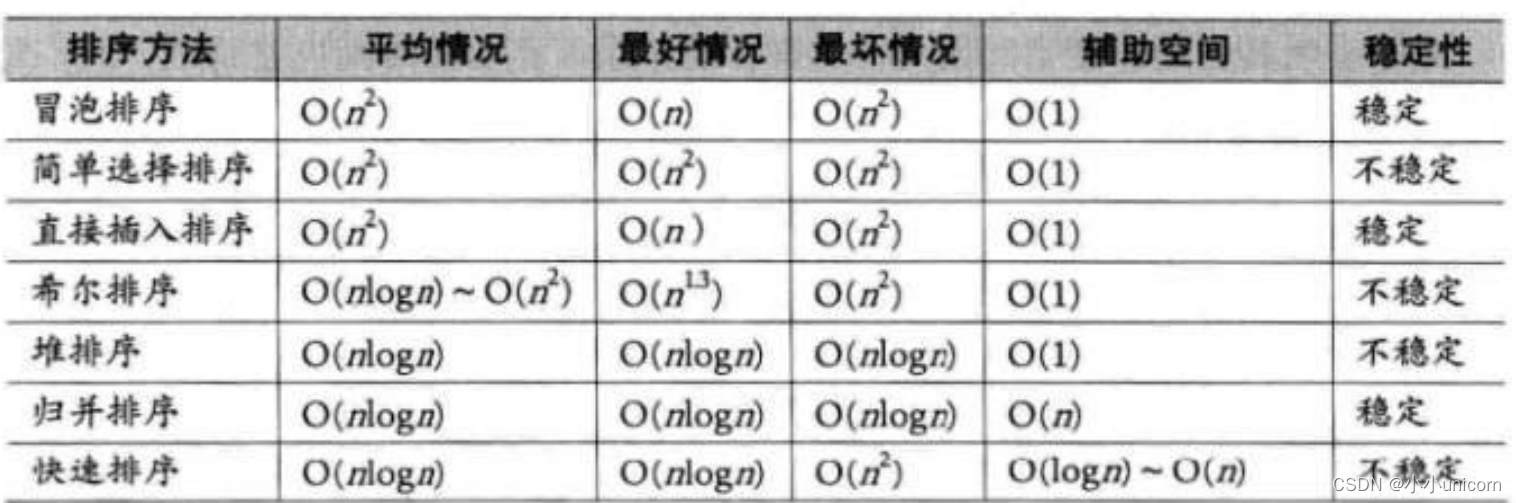
排序算法复杂度及稳定性分析