数据结构-----平衡二叉树

news2024/7/6 18:00:14

 目录

前言

1.平衡二叉树

1.1概念与特点

1.2与二叉排序树比较

1.3判断平衡二叉树

2.平衡二叉树的构建

2.1平衡因子 BF

2.2 LL型失衡（右旋）

2.3 RR型失衡（左旋）

2.4 LR型失衡（先左旋再右旋）

 2.5 RL型失衡（先右旋再左旋）

2.6构建平衡二叉树代码实现

 3.删除节点操作

3.1删除叶子节点

​编辑

3.2删除只有一个左（右）子树的节点

3.3删除有左右子树的节点

​编辑

3.4删除节点代码实现

4.平衡二叉树相关操作

4.1查找数据

4.2判断是否为平衡二叉树

4.3中序遍历输出

4.4销毁平衡二叉树

前言

        前面我发布了一篇介绍二叉排序树的相关文章，那么今天我们学习一种新的树----平衡二叉树，在此之前我们要学习过二叉排序树，才能更好的去学习平衡二叉树，平衡二叉树是二叉排序树的进一步优化，下面就一起来看看吧！

1.平衡二叉树

1.1概念与特点

        在计算机科学中，AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis，他们在1962年的论文《An algorithm for the organization of information》中发表了它。

二叉排序树相关链接：数据结构-----二叉排序树_Gretel Tade的博客-CSDN博客 

 特性：

  • 平衡二叉树是一个二叉排序树
  • 它的左子树和右子树都是平衡二叉树
  • 左右子树高度之差（简称平衡因子）的绝对值不超过 1（即：-1，0，1）

 如图所示: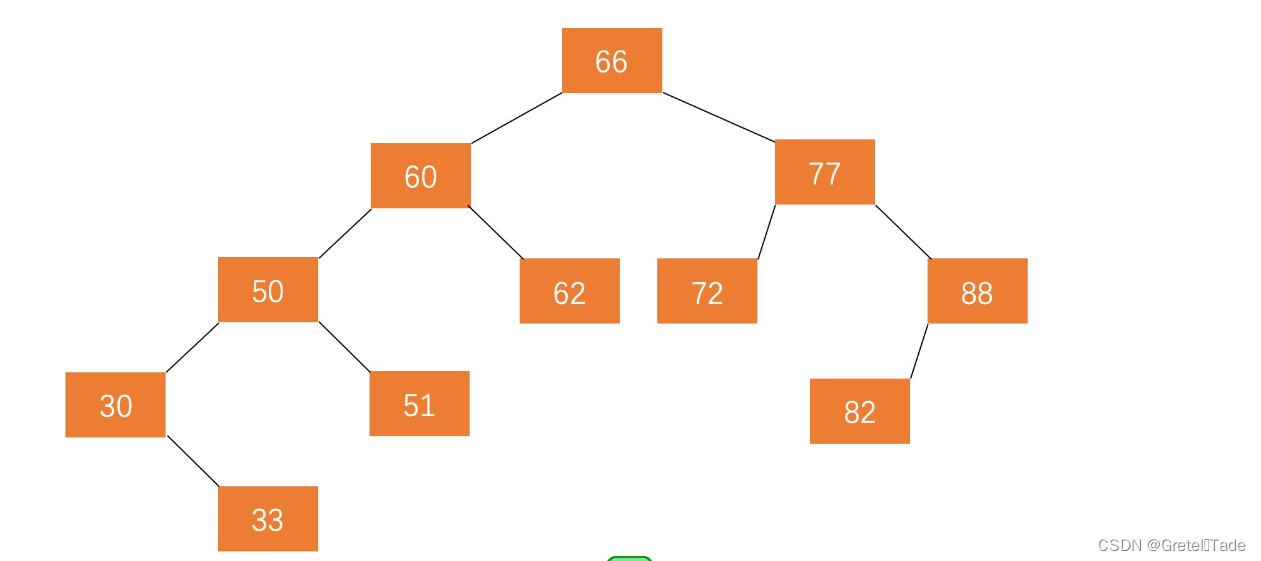

1.2与二叉排序树比较

在此之前我们学习过了二叉排序树的相关知识点，二叉排序树又名为二叉搜索树，但是当一个二叉排序树的形态是一个链状的话，那么搜索效率跟一个链表的搜索效率是毫无区别的，但是如果是一个平衡二叉树就不同了，因为平衡二叉树规定了左右子树高度差不会大于1，这样就可以大大提高了搜索的效率，下面看比较：

当前我插入[1,2,3,4,5,6] 这一数组构建一个二叉排序树的时候，其形态是如下图所示，很明显是一个链态的，无异于一个链表，当我要去搜索数字6的时候，就要遍历到最后一个数字，搜索效率为 O(n)。 

但是如果我通过构建平衡二叉树来储存这些数据的话，那就会有很大的不同，如下图所示，当我要去搜索最后一个节点的时候，就不需要去遍历这么多节点了，可以这么说，平衡二叉树是排序二叉树的优化结果。

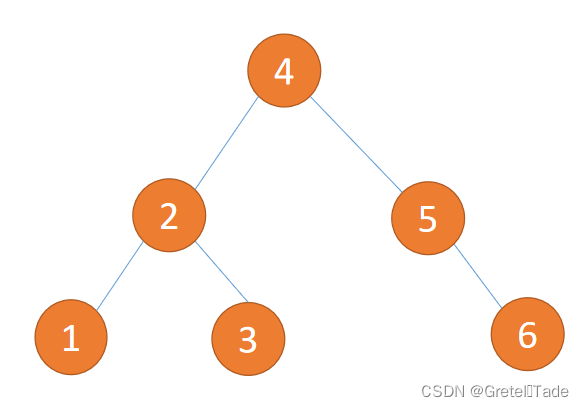
1.3判断平衡二叉树

  • 1. 是二叉排序树
  • 2. 任何一个节点的左子树或者右子树都是平衡二叉树，而且左右高度差小于等于 1

（1）这个不是平衡二叉树， 因为右子树比左子树高度差大于2

（2）这个不是平衡二叉树，因为没有符合二叉排序树的要求

（3）这个是平衡二叉树，既满足二叉排序树的要求，而且左右子树高度差小于2.

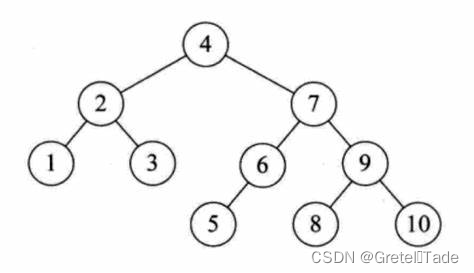
2.平衡二叉树的构建

        前面去构建一个二叉排序树，非常简单，只需要排序就行了，那构建一个平衡二叉树不仅仅要考虑到排序问题，还要考虑到左右子树高度不大于1才行，下面我介绍一种通过旋转的方法来去构建平衡二叉树。

2.1平衡因子 BF

定义：左子树和右子树高度差

计算方法：左子树高度减右子树高度的绝对值

 当满足BF<=1的时候，这个树就满足平衡条件。当不满足平衡条件的话，那就只能去通过旋转来实现平衡。下面有4种不满足平衡条件的情况，如图所示：

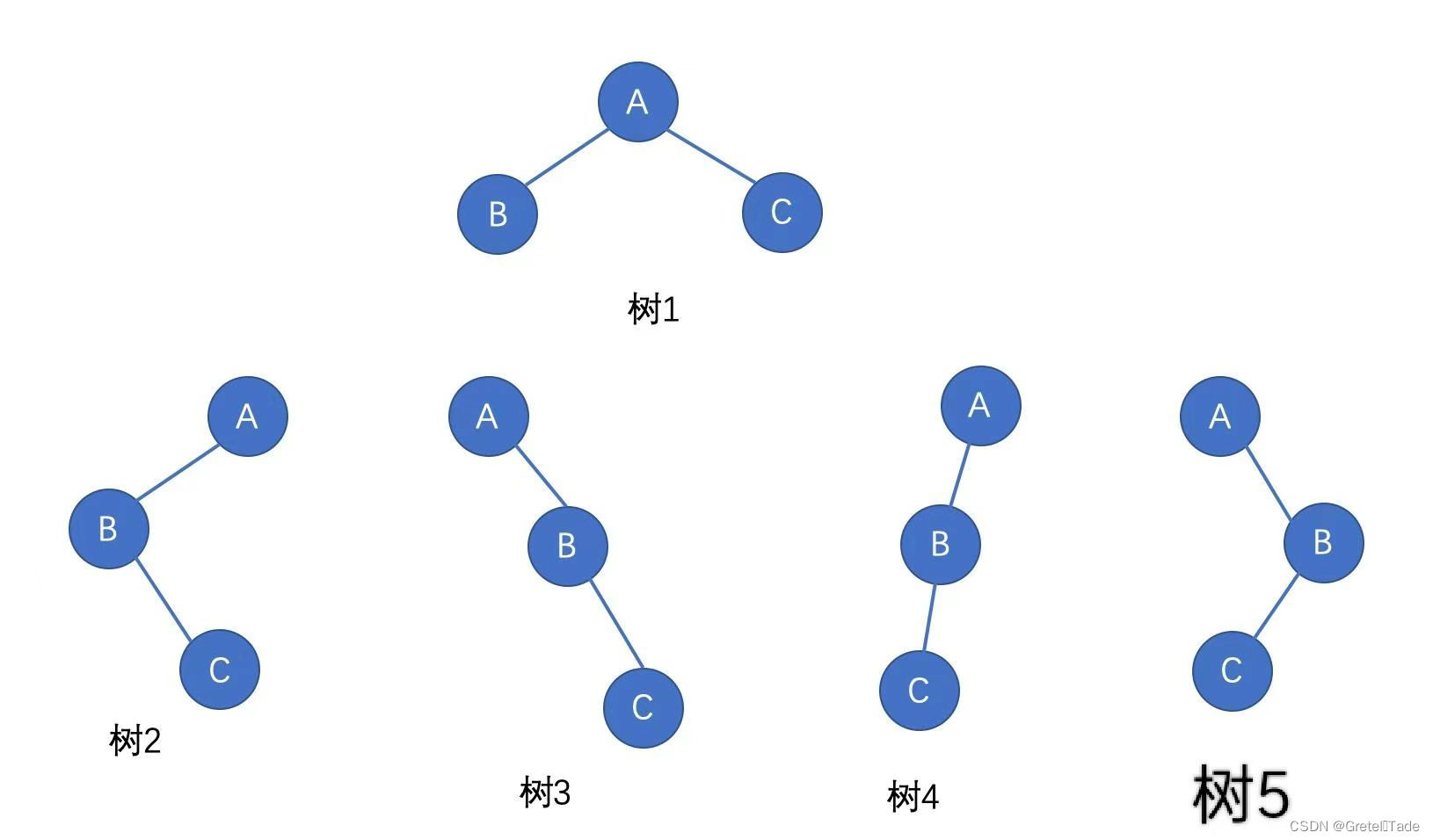
 树1是满足平衡条件的情况；

树2是在左子树右子节点出现失衡情况，属于 LR型

树3是在右子树右子节点出现失衡情况，属于 RR型

树4是在左子树左子节点出现失衡情况，属于 LL型

树5是在右子树左子节点出现失衡情况，属于 LR型

下面我就一一讲解怎么去通过旋转来处理上面这四种失衡问题。

2.2 LL型失衡（右旋）

 右旋就是通过顺时针旋转来实现平衡，就是处于右边的根结点落下变为叶子节点，而中间的节点变为新的根节点，最左边的叶子节点保持不变，最后形成新的结构。

动图演示：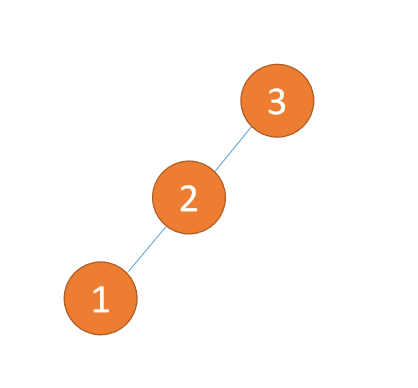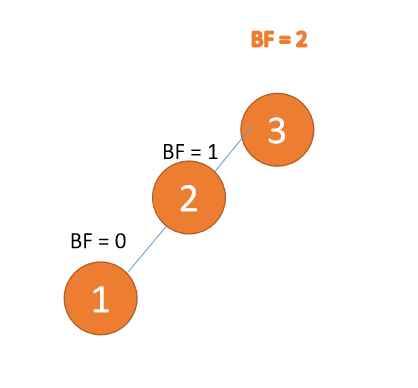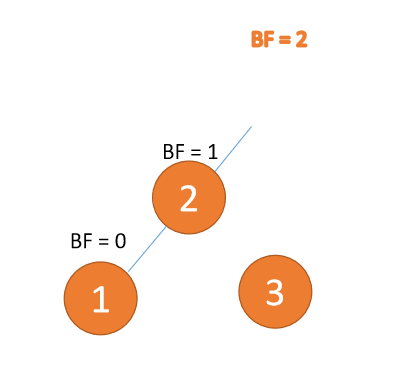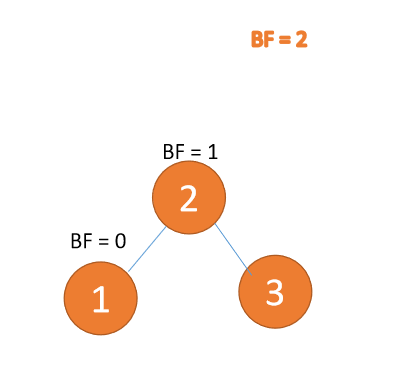

2.3 RR型失衡（左旋）

对于RR型失衡，通过逆时针旋转，最左边的根结点落下，变成叶子节点，中间的节点变为新的根节点，最右边的叶子节点保持不变。

动图演示：

2.4 LR型失衡（先左旋再右旋）

对于LR型失衡，先在根节点左子树进行左旋处理，变成LL型失衡，然后再去通过右旋来实现整体平衡。动图演示如下：

 先左旋：

再右旋: 

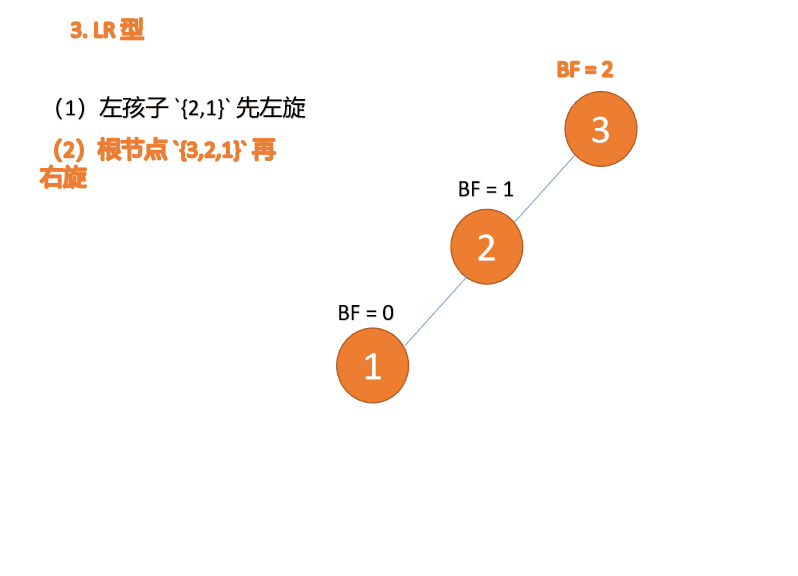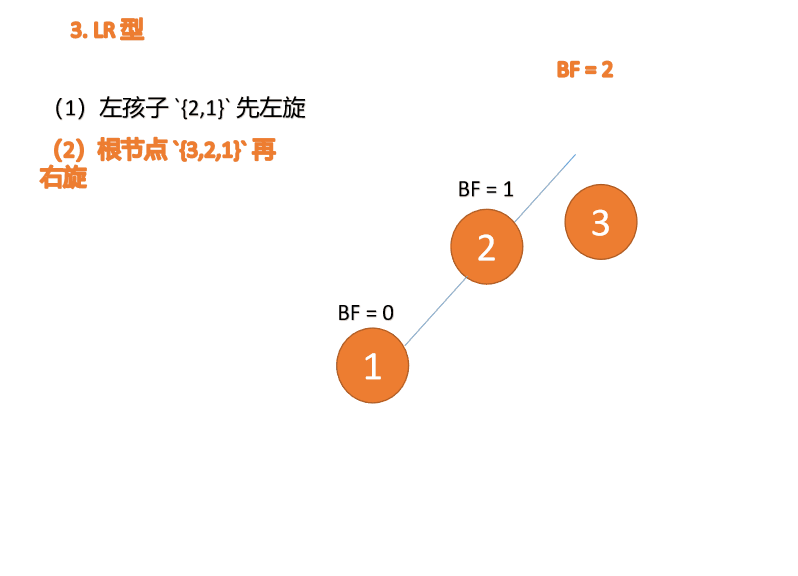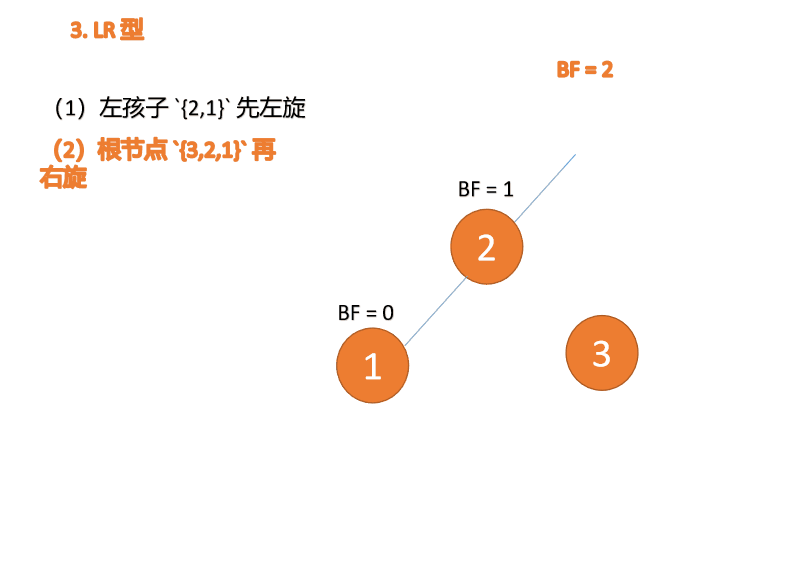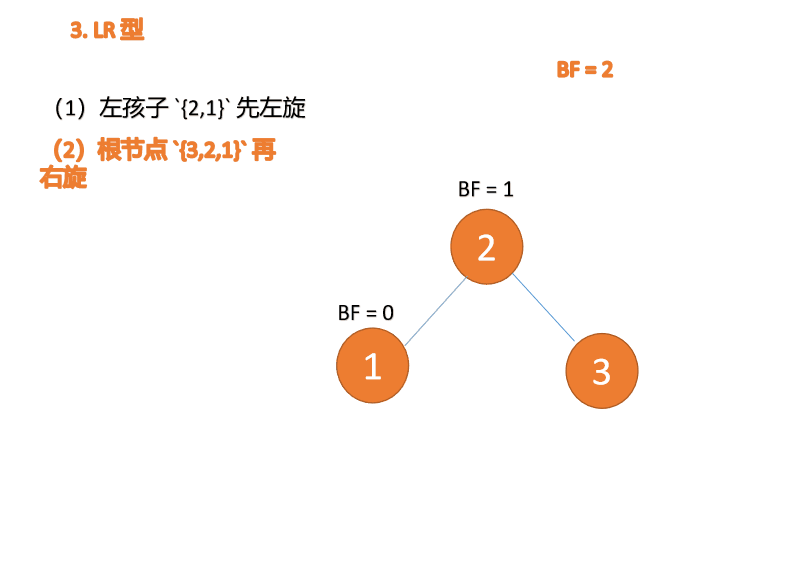
 2.5 RL型失衡（先右旋再左旋）

对于RL型失衡，在根节点的右子树先进行右旋处理，形成RR型失衡，然后整体进行左旋处理，最后达到平衡状态，动态演示如下：

先右旋： 

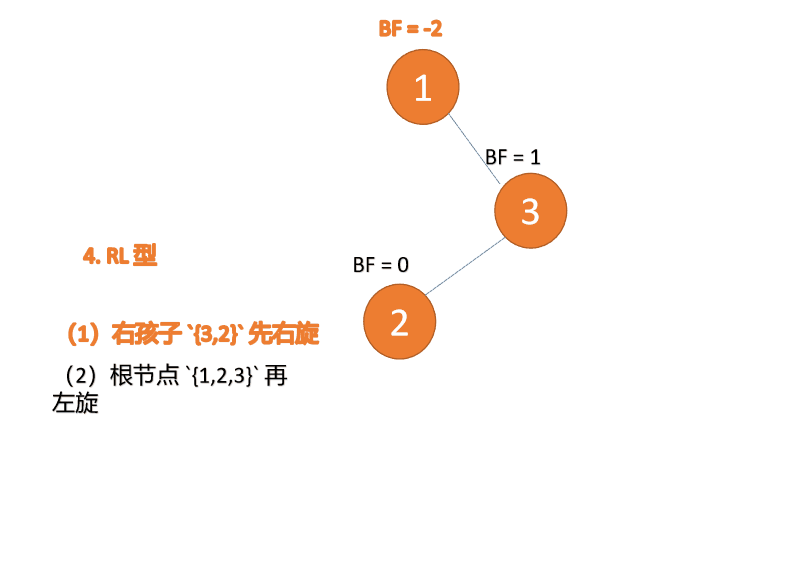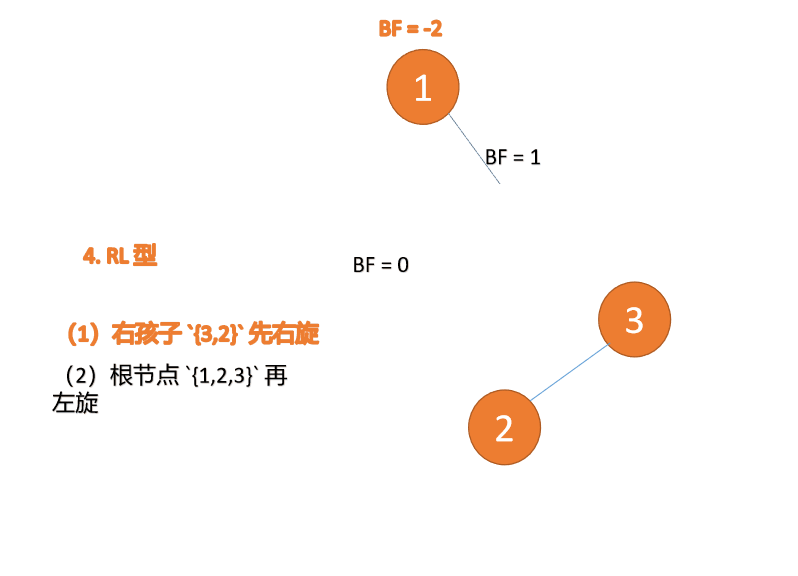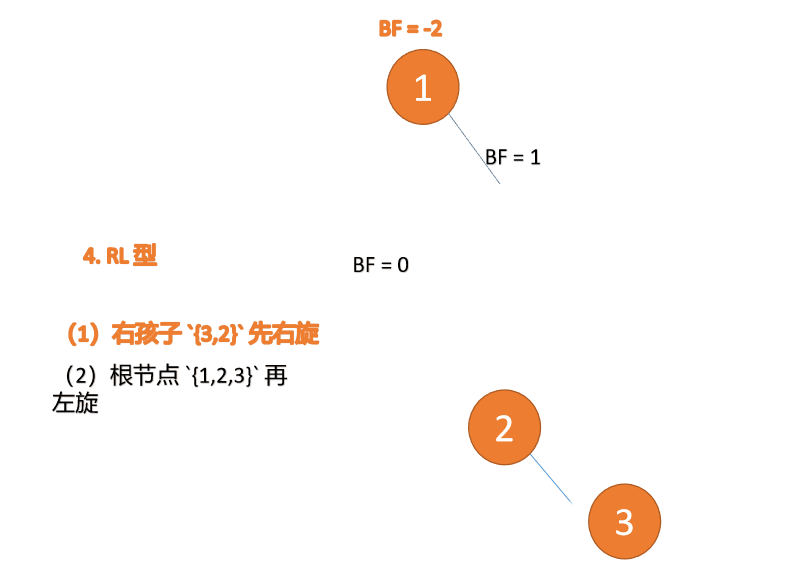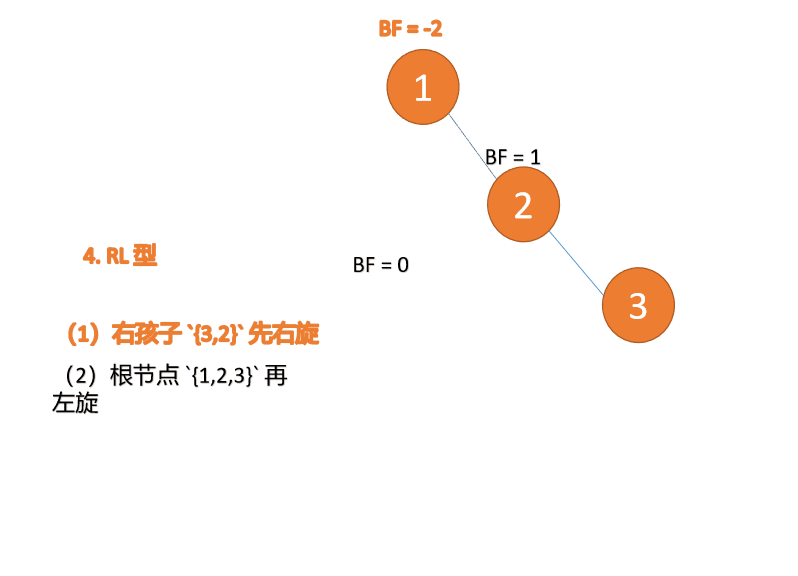 再左旋：

2.6构建平衡二叉树代码实现

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>

typedef int	Datatype;
typedef struct AVLtree {
	Datatype data;
	int heigh;//高度
	struct AVLtree* left;
	struct AVLtree* right;
}Node;

//绝对值
int abs(int a, int b) {
	return a - b > 0 ? a - b : b - a;
}

//创建一个节点
Node* Create_node(Datatype data) {
	Node* new_node = (Node*)malloc(sizeof(Node));
	if (!new_node) {
		printf("ERROR\n");
		exit(-1);
	}
	new_node->data = data;
	new_node->left = new_node->right = NULL;
	new_node->heigh = 0;
	return new_node;
}


//获取高度
int get_height(Node* T) {
	if (!T)
		return 0;
	else
		return T->heigh;
}


//1.插入右子树右节点，右旋
void right_rigth(Node** root) {
	Node* k = (*root)->right;
	(*root)->right = k->left;
	k->left = (*root);
	k->heigh = get_height(k->left) > get_height(k->right) ? get_height(k->left) : get_height(k->right);
	(*root)->heigh = get_height((*root)->left) > get_height((*root)->right) ? get_height((*root)->left) : get_height((*root)->right);
	*root = k;
}
//2.插入左子树左节点，失去平衡，左旋
void left_left(Node** root) {
	Node* k = (*root)->left;
	(*root)->left = k->right;
	k->right = (*root);
	k->heigh = get_height(k->left) > get_height(k->right) ? get_height(k->left) : get_height(k->right);
	(*root)->heigh = get_height((*root)->left) > get_height((*root)->right) ? get_height((*root)->left) : get_height((*root)->right);
	*root = k;
}
//3.插入左子树，右节点，失去平衡，先右旋再左旋
void left_right(Node** root) {
	right_rigth(&((*root)->left));
	left_left(&(*root));
}
//4.插入右子树左节点，失去平衡，先左旋再右旋
void rigth_left(Node** root) {
	left_left(&((*root)->right));
	right_rigth(&(*root));
}


//插入节点
void Insert_node(Datatype data, Node** root) {
	if (!(*root)) {
		(*root) = Create_node(data);
		return;
	}
	else {
		if (data < (*root)->data) {
			Insert_node(data, &((*root)->left));
			if (get_height((*root)->left) - get_height((*root)->right) > 1) {//如果出现失衡的情况
				if(data<(*root)->left->data)
					left_left(&(*root));
				else
					left_right(&(*root));
			}
		}
		else if (data > (*root)->data) {
			Insert_node(data, &((*root)->right));
			if (get_height((*root)->right) - get_height((*root)->left) > 1) {//如果出现失衡的情况
				if(data>(*root)->right->data)
					right_rigth(&(*root));
				else
					rigth_left(&(*root));
			}
		}
		else {
			printf("Do not insert numbers of the same size!\n");
			return;
		}
	}
	(*root)->heigh++;
}

//创建平衡二叉树
void Create_AVLtree(Node** T, Datatype* data,int n) {
	if (!data) {
		return;
	}
	for (int i = 0; i < n; i++) {
		Insert_node(data[i],T);
	}
}

 3.删除节点操作

在对平衡二叉树进行删除节点的操作时候，跟插入节点也是一样的，会出现失衡的情况，那这里就要通过旋转来去处理了，要进行那种旋转就要根据删除的节点属性去看，以下有4种情况：

  • 删除叶子结点
  • 删除结点只有左子树
  • 删除结点只有右子树
  • 删除结点有左、右子树

下面就一个一个来看，怎么去进行删除吧

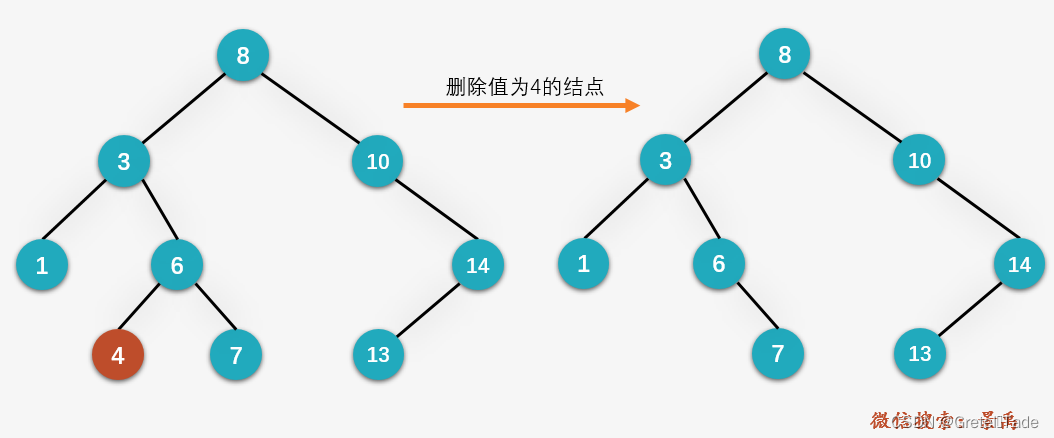
3.1删除叶子节点

删除叶子节点后要看，平衡二叉树是否失衡，如果没有失衡就直接删除即可；如果出现了失衡的情况就要从根节点开始向上依次检索看从哪个位置开始失衡了，一经发现失衡就进行相对于的旋转处理，直到根结点为止。

3.2删除只有一个左（右）子树的节点

这种情况就要用这个被删除节点的相邻节点来去顶替这个节点，然后整体进行相对于的旋转操作。如下图所示：

3.3删除有左右子树的节点

 要删除的节点有左右子树的话，那么就找到左子树的最大节点或者找到右子树最小节点来替换掉这个节点，然后把这个节点的空间释放掉就行了。

3.4删除节点代码实现

//查找数据节点
Node* Search_node(Node *T,Datatype target) {
	if (!T) {
		return NULL;
	}
	if (target == T->data)
		return T;
	else if (target < T->data)
		Search_node(T->left, target);
	else
		Search_node(T->right, target);
}

//删除指定数据的节点
void Del_node(Node** T, Datatype target) {
	Node* dnode = Search_node(*T, target);
	if (!dnode){//如果查找不成功，就返回
		printf("bye~~~error\n");
		return;
	}
	if (target < (*T)->data) {
		Del_node(&(*T)->left, target);
		if (get_height((*T)->left) - get_height((*T)->right) > 1) {
			if (target < (*T)->left->data)
				left_left(&*T);
			else
				left_right(&*T);
		}
	}
	else if (target > (*T)->data) {
		Del_node(&(*T)->right, target);
		if (get_height((*T)->right) - get_height((*T)->left) > 1) {
			if (target < (*T)->right->data)
				rigth_left(&*T);
			else
				right_rigth(&*T);
		}
	}
	//此时(*T)就是要删除的节点
	//1.如果这个节点都有左右子树的话
	else if ((*T)->left && (*T)->right) {
		//找到右子树最左边的节点，也就是比这个要删除节点大一位的节点
		Node* min = (*T)->right;
		while (min->left)
			min = min->left;
		(*T)->data = min->data;
		Del_node(&(*T)->right, min->data);
	}
	//2.如果这个节点有一个左右子树或者没有子树的情况
	else {
		Node* dnode = (*T);
		(*T) = (*T)->left ? (*T)->left : (*T)->right;//把这个节点进行替换掉
		free(dnode);//释放空间，删除这个节点
	}
	//高度重新处理
	if((*T))
		(*T)->heigh=get_height((*T)->left)>get_height((*T)->right)? 
		get_height((*T)->left)+1: get_height((*T)->right)+1;
}

4.平衡二叉树相关操作

4.1查找数据

查找数据然后返回这个节点，我们直接通过二分查找就行了，代码如下：

//查找数据节点
Node* Search_node(Node *T,Datatype target) {
	if (!T) {
		return NULL;
	}
	if (target == T->data)
		return T;
	else if (target < T->data)
		Search_node(T->left, target);
	else
		Search_node(T->right, target);
}

4.2判断是否为平衡二叉树

根据平衡二叉树的特性，我们需要判断这个二叉树是否排序，是否满足左右子树高度差不大于1 ,这里就需要用到递归一层一层检索了，最后取和运算，代码如下：

//判断一个树是否为平衡二叉树
bool Judge(Node* T) {
	if (!T){
		printf("NULL\n");
		exit(0);
	}
	if(T->left->data>T->data||T->right->data<T->data)
		return false;
	if (abs(get_height(T->left) - get_height(T->right)) > 1)
		return false;
	else
		return true;
	return Judge(T->left)&&Judge(T->right);
}

4.3中序遍历输出

//中序遍历输出
void In_travel(Node* T) {
	if (!T)
		return;
	In_travel(T->left);
	printf("%d ", T->data);
	In_travel(T->right);
}

4.4销毁平衡二叉树

销毁平衡二叉树就要把每一个节点的空间释放掉，那就直接从下往上去释放空间，代码如下：

//销毁
void Destroy(Node** T) {
	if (!*T)
		return;
	Destroy(&(*T)->left);
	Destroy(&(*T)->right);
	free(*T);
}

以上就是本期的全部内容了，我们下一期再见！

分享一张壁纸： 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1060619.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

springboot 集成 PageHelper 分页失效

springboot 集成 PageHelper 分页失效

前言 项目启动初期&#xff0c;在集成mybatis的分页插件&#xff0c;自定义封装了一个分页的工具类&#xff0c;方便后期项目的扩展。部分的代码如下&#xff1a; /*** 分页查询* 进行count计算** param pageNum 页数* param pageSize 每页数量* param supplier 查询操作* re…
阅读更多...
Redis相关概念

Redis相关概念

1. 什么是Redis&#xff1f;它主要用来什么的&#xff1f; Redis&#xff0c;英文全称是Remote Dictionary Server&#xff08;远程字典服务&#xff09;&#xff0c;是一个开源的使用ANSI C语言编写、支持网络、可基于内存亦可持久化的日志型、Key-Value数据库&#xff0c;并提…
阅读更多...
基于Java的毕业设计选题管理系统设计与实现(源码+lw+部署文档+讲解等)

基于Java的毕业设计选题管理系统设计与实现(源码+lw+部署文档+讲解等)

文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序&#xff08;小蔡coding&#xff09;有保障的售后福利 代码参考源码获取 前言 &#x1f497;博主介绍&#xff1a;✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…
阅读更多...
44 二叉搜索树中第K个小的元素

44 二叉搜索树中第K个小的元素

二叉搜索树中第K个小的元素 题解1 中序遍历题解2 AVL&#xff08;手撕平衡二叉树&#xff1a;谢谢力扣官方&#xff09; 给定一个二叉搜索树的根节点 root &#xff0c;和一个整数 k &#xff0c;请你设计一个算法查找其中第 k 个最小元素&#xff08;从 1 开始计数&#xf…
阅读更多...
免杀对抗-成品EXE免杀-反特征码-通用跳转

免杀对抗-成品EXE免杀-反特征码-通用跳转

一、exe程序生成 1.使用如下shellcode加载器&#xff0c;生成c/c语言的exe程序 加载器&#xff1a;1.c #include <Windows.h> #include <stdio.h>#pragma comment(linker,"/section:.data,RWE")unsigned char shellcode[] 生成的shellcode;int main() { …
阅读更多...
【一、灵犀考试系统项目设计、框架搭建】

【一、灵犀考试系统项目设计、框架搭建】

一、创建数据库 1、打开power designer&#xff0c;新建数据库模型 2、新建数据表&#xff0c;以及关系 【注意】 图片的类型有两种&#xff1a;varbinary 和 image varbinary : 二进制字节流&#xff0c;可以自动控制长度 image : 最大可放2G图片 3、创建数据库&#…
阅读更多...
基于郊狼优化的BP神经网络（分类应用） - 附代码

基于郊狼优化的BP神经网络（分类应用） - 附代码

基于郊狼优化的BP神经网络&#xff08;分类应用&#xff09; - 附代码 文章目录 基于郊狼优化的BP神经网络&#xff08;分类应用&#xff09; - 附代码1.鸢尾花iris数据介绍2.数据集整理3.郊狼优化BP神经网络3.1 BP神经网络参数设置3.2 郊狼算法应用 4.测试结果&#xff1a;5.M…
阅读更多...
国庆假期作业day2

国庆假期作业day2

作业&#xff1a;创建一个双向链表&#xff0c;将26个英文字母通过头插的方式插入到链表中&#xff0c;通过尾删的方式将数据读取出来并删除 #ifndef _TEXT_H #define _TEXT_H #include<myhead.h> typedef int datatype; typedef struct dblist {union {datatype data;/…
阅读更多...
逆强化学习

逆强化学习

1.逆强化学习的理论框架 1.teacher的行为被定义成best 2.学习的网络有两个&#xff0c;actor和reward 3.每次迭代中通过比较actor与teacher的行为来更新reward function&#xff0c;基于新的reward function来更新actor使得actor获得的reward最大。 loss的设计相当于一个排序问…
阅读更多...
Java基于SSM的校园一卡通系统设计与实现

Java基于SSM的校园一卡通系统设计与实现

末尾获取源码 开发语言&#xff1a;Java Java开发工具&#xff1a;JDK1.8 后端框架&#xff1a;SSM 前端&#xff1a;采用JSP技术开发 数据库&#xff1a;MySQL5.7和Navicat管理工具结合 服务器&#xff1a;Tomcat8.5 开发软件&#xff1a;IDEA / Eclipse 是否Maven项目&#x…
阅读更多...
解决stm32驱动LCD1602A时不显示第二行的问题

解决stm32驱动LCD1602A时不显示第二行的问题

根据这个教程&#xff0c;用仿真测试可以成功&#xff0c;但实际上上真机只显示第一行。 考虑到可能是电压的问题&#xff0c;我外接的是和stm32一样的3.3v&#xff0c;但实际上lcd的额定电压是5v&#xff0c;于是换为5V&#xff0c;结果变这样了&#xff1a; 只能恢复电压3.…
阅读更多...
Linux信号解析

Linux信号解析

文章目录 Linux信号概念信号种类Linux信号产生异步 LInux信号阻塞递达、未决、阻塞、忽略信号集操作函数阻塞信号集操作函数未决信号集操作函数 Linux信号捕捉signal函数sigaction函数 总结 Linux信号概念 信号在我们的生活中无处不在&#xff0c;常见的如电话铃声&#xff0c…
阅读更多...
openstack-ansible部署zed版本all-in-one

openstack-ansible部署zed版本all-in-one

目录 部署架构部署节点准备安装Rocky linux 9配置rocky 目标节点配置网络配置rocky linux网卡的创建永久网桥的方法&#xff1a; 部署前配置 部署架构 可用的操作系统&#xff1a; Debian11&#xff08;bullseye&#xff09; Ubuntu 22.04或20.04 CentOS Stream 9 或 Rocky Lin…
阅读更多...
【Golang】网络编程

【Golang】网络编程

网络编程 网络模型介绍 OSI七层网络模型 在软件开发中我们使用最多的是上图中将互联网划分为五个分层的模型&#xff1a; 物理层数据链路层网络层传输层应用层 物理层 我们的电脑要与外界互联网通信&#xff0c;需要先把电脑连接网络&#xff0c;我们可以用双绞线、光纤、…
阅读更多...
CocosCreator3.8研究笔记（二十五）CocosCreator 动画系统-2d骨骼动画spine

CocosCreator3.8研究笔记（二十五）CocosCreator 动画系统-2d骨骼动画spine

大家都知道&#xff0c;在游戏中 一般用帧动画或者骨骼动画&#xff0c;实现 人物的行走、奔跑、攻击等动作。 帧动画&#xff0c;在上一篇已经做了介绍&#xff0c;感兴趣的朋友可以前往阅读&#xff1a; CocosCreator3.8研究笔记&#xff08;二十四&#xff09;CocosCreator …
阅读更多...
10.5作业

10.5作业

磕磕绊绊还是差不多完成了,tcp多客户端在线词典 代码&#xff1a; 数据库导入&#xff1a;有点粗糙&#xff0c;不知道怎么搞成两列&#xff0c;一个单词中间还是空格卧槽难搞 #include <stdio.h> #include <string.h> #include <stdlib.h> #include <s…
阅读更多...
NPDP产品经理知识(产品创新流程)

NPDP产品经理知识(产品创新流程)

1.复习组合管理： 组合管理的目标 ===> 价值最大化，项目平衡，战略一致，管道平衡(资源需求和供给)，盈利充分 (实现财务目标) 产品创新流程就是管理风险的过程。 模糊前端： 产品创新章程：PIC 包含 =====> 背景，聚焦舞台，目标和目的，特别准则，可持续性 新产…
阅读更多...
mysql面试题13：MySQL中什么是异步复制？底层实现？

mysql面试题13：MySQL中什么是异步复制？底层实现？

该文章专注于面试，面试只要回答关键点即可，不需要对框架有非常深入的回答，如果你想应付面试，是足够了，抓住关键点 面试官：讲一讲mysql中什么是异步复制？底层实现？ MySQL中的异步复制（Asynchronous Replication）是一种复制模式，主服务器将数据写入二进制日志后，无…
阅读更多...
计组——I/O方式

计组——I/O方式

一、程序查询方式 CPU不断轮询检查I/O控制器中“状态寄存器”&#xff0c;检测到状态为“已完成”之后&#xff0c;再从数据寄存器取出输入数据。 过程&#xff1a; 1.CPU执行初始化程序&#xff0c;并预置传送参数&#xff1b;设置计数器、设置数据首地址。 2. 向I/O接口发…
阅读更多...
星际争霸之小霸王之小蜜蜂（十六）--狂奔的花猫

星际争霸之小霸王之小蜜蜂（十六）--狂奔的花猫

系列文章目录 星际争霸之小霸王之小蜜蜂&#xff08;十五&#xff09;--剧将终场 星际争霸之小霸王之小蜜蜂&#xff08;十四&#xff09;--资本家的眼泪 星际争霸之小霸王之小蜜蜂&#xff08;十三&#xff09;--接着奏乐接着舞 星际争霸之小霸王之小蜜蜂&#xff08;十二…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023