原文链接:https://openreview.net/pdf?id=1FvkSpWosOl https://openreview.net/pdf?id=1FvkSpWosOl
https://openreview.net/pdf?id=1FvkSpWosOl
代码库:GitHub - Gsunshine/Enjoy-Hamburger: [ICLR 2021 top 3%] Is Attention Better Than Matrix Decomposition?[ICLR 2021 top 3%] Is Attention Better Than Matrix Decomposition? - GitHub - Gsunshine/Enjoy-Hamburger: [ICLR 2021 top 3%] Is Attention Better Than Matrix Decomposition? https://github.com/Gsunshine/Enjoy-Hamburger
https://github.com/Gsunshine/Enjoy-Hamburger
0.摘要
作为现代深度学习中的重要组成部分,特别是自注意力机制,在全局相关性发现中起着至关重要的作用。然而,在建模全局上下文时,手工设计的注意力机制是否不可替代?我们有趣的发现是,自注意力并不比20年前开发的矩阵分解(MD)模型在编码长距离依赖性方面的性能和计算成本更好。我们将全局上下文问题建模为一个低秩完成问题,并展示其优化算法能够帮助设计全局信息块。本文提出了一系列汉堡包,其中我们利用优化算法来解决MD,将输入表示分解为子矩阵并重建一个低秩嵌入。当仔细处理通过MD反向传播的梯度时,具有不同MD的汉堡包可以在与流行的全局上下文模块自注意力竞争时表现出色。我们在需要学习全局上下文的视觉任务中进行了全面的实验,包括语义分割和图像生成,在性能上显著优于自注意力及其变种。代码已经提供。
1.引言
自从自注意力和Transformer(Vaswani et al.,2017)在捕捉长距离依赖性方面显示出明显优势后,注意力机制被广泛应用于计算机视觉(Wang et al.,2018; Zhang et al.,2019a)和自然语言处理(Devlin et al.,2019)中,用于全局信息挖掘。然而,在建模全局上下文时,手工设计的注意力机制是否不可替代?本文重点研究了一种设计全局上下文模块的新方法。关键思想是,如果我们将像全局上下文这样的归纳偏置形式化为目标函数,则最小化目标函数的优化算法可以构建一个计算图,即我们在网络中所需要的架构。我们通过为最具代表性的全局上下文模块自注意力开发一个对应模块来具体化这个思想。考虑到在网络中提取全局信息就像找到一个字典和相应的编码来捕捉内在关联性,我们将上下文发现建模为输入张量的低秩完成问题,并通过矩阵分解来解决。本文提出了一个全局相关性模块,即汉堡包,通过采用矩阵分解将学习到的表示分解为子矩阵,以恢复干净的低秩信号子空间。解决矩阵分解的迭代优化算法定义了中心计算图,即汉堡包的架构。我们的工作利用矩阵分解模型作为汉堡包的基础,包括向量量化(Vector Quantization,VQ)(Gray & Neuhoff,1998),概念分解(Concept Decomposition,CD)(Dhillon & Modha,2001)和非负矩阵分解(Non-negative Matrix Factorization,NMF)(Lee & Seung,1999)。此外,我们采用截断BPTT(Back-Propagation Through Time)算法(Werbos et al.,1990)而不是直接应用于迭代优化的BPTT算法,即一步梯度,以有效地反向传播梯度。我们在全局信息被证明至关重要的基本视觉任务中,包括语义分割和图像生成,展示了汉堡包的优势。实验证明,经过优化设计的汉堡包在避免通过MD的迭代计算图反向传播的不稳定梯度时,可以与最先进的注意力模型竞争。汉堡包在PASCAL VOC数据集(Everingham et al.,2010)和PASCAL Context数据集(Mottaghi et al.,2014)上为语义分割设立了新的最先进记录,并在ImageNet(Deng et al.,2009)上的大规模图像生成中超越了现有的注意力模块。
本文的贡献如下:
- 我们展示了一种白盒方法来设计全局信息模块,即通过将最小化目标函数的优化算法转化成架构,其中将全局相关性建模为低秩完成问题。
- 我们提出了一种轻量而强大的全局上下文模块Hamburger,其复杂度为O(n),在语义分割和图像生成等任务上超越了各种注意力模块。
- 我们发现将MD应用于网络中的主要障碍是其迭代优化算法中不稳定的反向梯度。作为一种实用的解决方案,我们提出的一步梯度有助于使用MD训练Hamburger。
2.方法学
2.1.预热
矩阵分解在提出的Hamburger中起着关键作用,我们首先回顾一下矩阵分解的思想。常见的观点是,矩阵分解将观察到的矩阵分解为几个子矩阵的乘积,例如奇异值分解。然而,更有启发性的观点是,通过假设生成过程,矩阵分解作为生成的逆过程,将组成复杂数据的原子分解开来。通过重建原始矩阵,矩阵分解可以恢复观察到的数据的潜在结构。假设给定的数据被排列成一个大矩阵X=[x1;···;xn]∈R^d×n,一个通用的假设是,存在一个低维子空间或多个子空间的并集隐藏在X中。也就是说,存在一个字典矩阵D=[d1;···;dr]∈R^d×r和相应的编码C=[c1;···;cn]∈R^r×n,使得X可以表示为 其中,X̄ ∈ Rd×n 是输出的低秩重建矩阵,E ∈ Rd×n 是要丢弃的噪声矩阵。我们假设恢复的矩阵X̄具有低秩性质,即 rank(X̄) ≤ min(rank(D), rank(C)) ≤ r ≤ min(d, n)。通过对矩阵D、C和E假设结构,可以得到不同的矩阵分解方法 (Kolda & Bader, 2009; Udell et al., 2016)。矩阵分解通常被建模为具有各种约束的目标函数,并通过优化算法进行求解,经典应用包括图像去噪 (Wright et al., 2009; Lu et al., 2014)、修复 (Mairal et al., 2010)和特征提取 (Zhang et al., 2012)。
其中,X̄ ∈ Rd×n 是输出的低秩重建矩阵,E ∈ Rd×n 是要丢弃的噪声矩阵。我们假设恢复的矩阵X̄具有低秩性质,即 rank(X̄) ≤ min(rank(D), rank(C)) ≤ r ≤ min(d, n)。通过对矩阵D、C和E假设结构,可以得到不同的矩阵分解方法 (Kolda & Bader, 2009; Udell et al., 2016)。矩阵分解通常被建模为具有各种约束的目标函数,并通过优化算法进行求解,经典应用包括图像去噪 (Wright et al., 2009; Lu et al., 2014)、修复 (Mairal et al., 2010)和特征提取 (Zhang et al., 2012)。
2.2.提出的方法
我们专注于为无需费力手工设计的网络构建全局上下文模块。在开始讨论之前,我们简要回顾了代表性的手工设计的上下文块——自注意力机制。注意机制旨在从大量无意识的上下文中找到一组概念,以进行进一步的有意识推理 (Xu et al., 2015; Bengio, 2017; Goyal et al., 2019)。作为一个代表性的例子,自注意力机制 (Vaswani et al., 2017) 被提出用于学习机器翻译中的长程依赖关系。 其中,Q、K、V ∈ R^n×d 是通过线性变换从输入中投影出来的特征。自注意力机制通过同时关注所有标记,而不是逐一处理的循环神经网络,从而提取全局信息。
其中,Q、K、V ∈ R^n×d 是通过线性变换从输入中投影出来的特征。自注意力机制通过同时关注所有标记,而不是逐一处理的循环神经网络,从而提取全局信息。 尽管自注意力及其变种取得了巨大的成功,但研究人员面临两个问题:一是基于自注意力进行新的全局上下文模块开发,通常需要手工设计;二是解释当前注意力模型的工作原理。本文绕过这两个问题,并找到了一种通过定义明确的白盒工具包来轻松设计全局上下文模块的方法。我们试图将人类归纳偏见(如全局上下文)形式化为一个目标函数,并使用优化算法来解决这个问题,以设计模块的架构。优化算法创建一个计算图,接受一些输入,并最终输出解决方案。我们将优化算法的计算图应用于我们上下文模块的核心部分。基于这种方法,我们需要将网络的全局信息问题建模为一个优化问题。以卷积神经网络(CNN)为例进行进一步讨论。在我们将图像输入网络后,网络输出一个张量X∈R^C×H×W。由于张量可以看作是一个HW个C维超像素的集合,我们将张量展开成一个矩阵X∈R^C×HW。当模块学习长程依赖或全局上下文时,隐藏的假设是超像素之间存在固有的相关性。为了简化起见,我们假设超像素是线性相关的,这意味着X中的每个超像素都可以表示为基向量的线性组合,而基向量的元素通常远小于HW。在理想情况下,X中隐藏的全局信息可以是低秩的。然而,由于传统CNN对于建模全局上下文的能力较差(Wang et al., 2018; Zhang et al., 2019a),学习得到的X通常会受到冗余信息或不完整性的干扰。上述分析提出了一种潜在的方法来建模全局上下文,即通过完成展开矩阵X中的低秩部分X̄,丢弃噪声部分E,使用Eq.(1)中描述的经典矩阵分解模型来同时过滤冗余和不完整性。因此,我们将学习全局上下文建模为一个低秩完成问题,并将矩阵分解作为其解决方案。根据第2.1节的概念,矩阵分解的一般目标函数为
尽管自注意力及其变种取得了巨大的成功,但研究人员面临两个问题:一是基于自注意力进行新的全局上下文模块开发,通常需要手工设计;二是解释当前注意力模型的工作原理。本文绕过这两个问题,并找到了一种通过定义明确的白盒工具包来轻松设计全局上下文模块的方法。我们试图将人类归纳偏见(如全局上下文)形式化为一个目标函数,并使用优化算法来解决这个问题,以设计模块的架构。优化算法创建一个计算图,接受一些输入,并最终输出解决方案。我们将优化算法的计算图应用于我们上下文模块的核心部分。基于这种方法,我们需要将网络的全局信息问题建模为一个优化问题。以卷积神经网络(CNN)为例进行进一步讨论。在我们将图像输入网络后,网络输出一个张量X∈R^C×H×W。由于张量可以看作是一个HW个C维超像素的集合,我们将张量展开成一个矩阵X∈R^C×HW。当模块学习长程依赖或全局上下文时,隐藏的假设是超像素之间存在固有的相关性。为了简化起见,我们假设超像素是线性相关的,这意味着X中的每个超像素都可以表示为基向量的线性组合,而基向量的元素通常远小于HW。在理想情况下,X中隐藏的全局信息可以是低秩的。然而,由于传统CNN对于建模全局上下文的能力较差(Wang et al., 2018; Zhang et al., 2019a),学习得到的X通常会受到冗余信息或不完整性的干扰。上述分析提出了一种潜在的方法来建模全局上下文,即通过完成展开矩阵X中的低秩部分X̄,丢弃噪声部分E,使用Eq.(1)中描述的经典矩阵分解模型来同时过滤冗余和不完整性。因此,我们将学习全局上下文建模为一个低秩完成问题,并将矩阵分解作为其解决方案。根据第2.1节的概念,矩阵分解的一般目标函数为 其中,L是重构损失,R1和R2是字典D和代码C的正则化项。将最小化Eq.(4)的优化算法表示为M。M是我们在全局上下文模块中使用的核心架构。为了帮助读者进一步理解这个建模过程,我们在附录G中提供了更直观的说明。在后面的章节中,我们介绍了我们的全局上下文块Hamburger,并讨论了M的详细MD模型和优化算法。最后,我们解决了通过矩阵分解进行反向传播的梯度问题。
其中,L是重构损失,R1和R2是字典D和代码C的正则化项。将最小化Eq.(4)的优化算法表示为M。M是我们在全局上下文模块中使用的核心架构。为了帮助读者进一步理解这个建模过程,我们在附录G中提供了更直观的说明。在后面的章节中,我们介绍了我们的全局上下文块Hamburger,并讨论了M的详细MD模型和优化算法。最后,我们解决了通过矩阵分解进行反向传播的梯度问题。
2.2.1.Hambuger
Hamburger由一片“火腿”(矩阵分解)和两片“面包”(线性变换)组成。顾名思义,Hamburger首先通过线性变换Wl将输入Z∈R^{dz×n}映射到特征空间中,即“下面包”,然后使用矩阵分解M来解决低秩信号子空间,对应于“火腿”,最后使用另一个线性变换Wu将提取的信号转换为输出,称为“上面包”。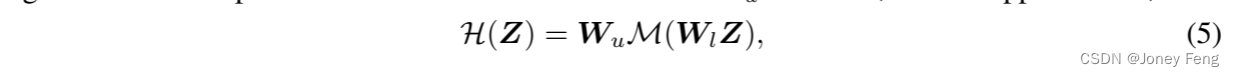 其中,矩阵分解M用于恢复清晰的潜在结构,起到全局非线性的作用。关于M的详细架构,即分解X的优化算法,在2.2.2节中进行了讨论。图1描述了Hamburger的架构,它通过批量归一化(BN)(Ioffe&Szegedy,2015)、跳跃连接与网络协作,并最终输出Y。
其中,矩阵分解M用于恢复清晰的潜在结构,起到全局非线性的作用。关于M的详细架构,即分解X的优化算法,在2.2.2节中进行了讨论。图1描述了Hamburger的架构,它通过批量归一化(BN)(Ioffe&Szegedy,2015)、跳跃连接与网络协作,并最终输出Y。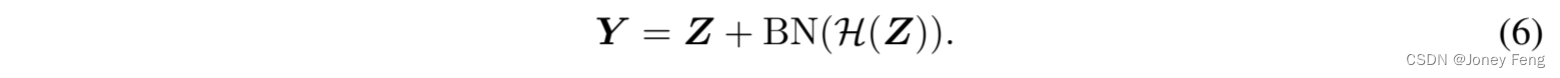
2.2.2.Hams
本节描述了“ham”的结构,即Eq.(5)中的M。如前一节所讨论的,通过将全局信息发现形式化为MD的优化问题,自然地可以将解决MD的算法组合成M。M以“下面包”的输出作为输入,并计算一个低秩重构作为其输出,分别表示为X和X̄。 我们研究了两种MD模型来解决D和C并重构X̄,分别为向量量化(VQ)和非负矩阵分解(NMF),而将概念分解(CD)留给附录B。选定的MD模型仅作简要介绍,因为我们致力于阐明低秩归纳偏差和基于优化的设计方法对全局上下文模块的重要性,而不是特定的MD模型。在本文的上下文中,更倾向于将MD部分作为一个整体,即M,并重点关注Hamburger如何展现其整体上的优势。
我们研究了两种MD模型来解决D和C并重构X̄,分别为向量量化(VQ)和非负矩阵分解(NMF),而将概念分解(CD)留给附录B。选定的MD模型仅作简要介绍,因为我们致力于阐明低秩归纳偏差和基于优化的设计方法对全局上下文模块的重要性,而不是特定的MD模型。在本文的上下文中,更倾向于将MD部分作为一个整体,即M,并重点关注Hamburger如何展现其整体上的优势。
向量量化(Vector Quantization,VQ)(Gray&Neuhoff,1998)是一种经典的数据压缩算法,可以通过矩阵分解的形式来表述为一个优化问题: 其中ei是单位基向量,ei =[0;···;1;···;0]>ith。为了最小化Eq.(8)中的目标函数,解决方案是K-means算法(Gray&Neuhoff,1998)。然而,为了确保VQ是可微的,我们用softmax和余弦相似度替换了硬arg min和欧氏距离,得到Alg.1,其中cosine(D;X)是一个相似度矩阵,其元素满足cosine(D;X)ij =kdd>ikkxxjk,softmax是逐列应用的,并且T是温度参数。当T不等于0时,我们可以通过一个one-hot向量得到一个硬分配。
其中ei是单位基向量,ei =[0;···;1;···;0]>ith。为了最小化Eq.(8)中的目标函数,解决方案是K-means算法(Gray&Neuhoff,1998)。然而,为了确保VQ是可微的,我们用softmax和余弦相似度替换了硬arg min和欧氏距离,得到Alg.1,其中cosine(D;X)是一个相似度矩阵,其元素满足cosine(D;X)ij =kdd>ikkxxjk,softmax是逐列应用的,并且T是温度参数。当T不等于0时,我们可以通过一个one-hot向量得到一个硬分配。 如果我们对字典D和编码C施加非负约束,就得到了非负矩阵分解(Non-negative Matrix Factorization,NMF)(Lee&Seung,1999):
如果我们对字典D和编码C施加非负约束,就得到了非负矩阵分解(Non-negative Matrix Factorization,NMF)(Lee&Seung,1999): 为了满足非负约束,在将X输入NMF之前,我们在其上添加了ReLU非线性函数。我们采用了乘法更新(Multiplicative Update)规则(Lee&Seung,2001)来解决NMF,这保证了收敛性。作为白盒全局上下文模块,VQ、CD和NMF都直观且轻量,表现出了显著的效率。它们被转化为主要由矩阵乘法组成的优化算法,其复杂度为O(ndr),比自注意力中的O(n2d)复杂度要低得多,其中r << n。这三种MD都很友好地使用内存,因为它们避免生成一个大的n×n矩阵作为中间变量,就像自注意力中的Q和K的乘积在Eq.(3)中一样。在后面的部分,我们的实验证明,尽管M的架构是通过优化创建的,并且与经典的点积自注意力看起来不同,但MD至少与自注意力不相上下。
为了满足非负约束,在将X输入NMF之前,我们在其上添加了ReLU非线性函数。我们采用了乘法更新(Multiplicative Update)规则(Lee&Seung,2001)来解决NMF,这保证了收敛性。作为白盒全局上下文模块,VQ、CD和NMF都直观且轻量,表现出了显著的效率。它们被转化为主要由矩阵乘法组成的优化算法,其复杂度为O(ndr),比自注意力中的O(n2d)复杂度要低得多,其中r << n。这三种MD都很友好地使用内存,因为它们避免生成一个大的n×n矩阵作为中间变量,就像自注意力中的Q和K的乘积在Eq.(3)中一样。在后面的部分,我们的实验证明,尽管M的架构是通过优化创建的,并且与经典的点积自注意力看起来不同,但MD至少与自注意力不相上下。
2.3.一步梯度
由于M涉及到一个优化算法作为其计算图,将其融入网络的关键是如何迭代算法进行梯度反向传播。优化的类似RNN行为暗示了通过时间反向传播(Back-Propagation Through Time,BPTT)算法(Werbos et al.,1990)作为区分迭代过程的标准选择。我们首先回顾一下BPTT算法。然而,在实践中,BPTT带来的不稳定梯度对Hamburger的性能有害。因此,我们建立了一个抽象模型来分析BPTT的缺点,并尝试在考虑MD作为优化算法的性质时找到一个实用的解决方案。如图2所示,x,y和ht分别表示时间步t的输入、输出和中间结果,F和G是运算符。在每个时间步,模型接收由底层网络处理的相同输入x。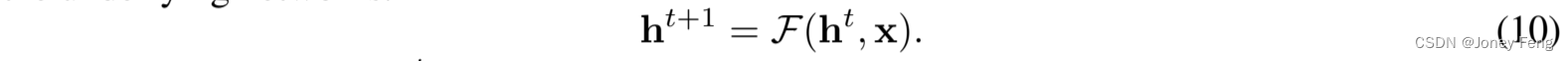 所有的中间结果hi都被丢弃了,只有最后一步的输出ht经过G生成输出y。
所有的中间结果hi都被丢弃了,只有最后一步的输出ht经过G生成输出y。 在BPTT算法中,根据链式法则,可以得到从输出y到输入x的梯度。
在BPTT算法中,根据链式法则,可以得到从输出y到输入x的梯度。 一个思维实验是考虑t趋向于无穷大,导致完全收敛的结果h∗和方程(12)中的无限项。我们假设F和G对于h具有常数Lh的Lipschitz连续性,对于x和LG的常数Lx和LG的Lipschitz连续性,且Lh < 1。需要注意的是,这些假设适用于很多优化或数值方法。然后我们有:
一个思维实验是考虑t趋向于无穷大,导致完全收敛的结果h∗和方程(12)中的无限项。我们假设F和G对于h具有常数Lh的Lipschitz连续性,对于x和LG的常数Lx和LG的Lipschitz连续性,且Lh < 1。需要注意的是,这些假设适用于很多优化或数值方法。然后我们有: 当Lh接近0时,很容易导致相对于h0的梯度消失,当Lh接近1时,很容易导致相对于x的梯度爆炸。此外,雅可比矩阵 @@yx 在Lh接近1时会出现病态条件的项(I −@@hF∗)−1,即@@Fh的最大特征值,即F相对于h的Lipschitz常数接近1,而其最小特征值通常接近0,从而限制了梯度在参数空间中搜索良好泛化解的能力。梯度通过优化算法反向传播的不规则尺度和频谱表明,直接将BPTT应用于Hamburger是不可行的,这在使用与第3.1节相同的消融设置的实验中得到了证实(见表1)。这种分析启发了我们一个可能的解决方案。需要注意的是,在BPTT算法中,存在多个雅可比矩阵的乘法 @hj @hj−@hj @hj−1 和无穷级数的求和,导致梯度的尺度无法控制。这启示我们在保留主导项的同时去除一些次要项,以确保梯度的方向大致正确。考虑将式(12)的项视为级数,即f@@hyt Qt j−=1t−i @@hhj+1 j @h@tx−i gi,如果其项的尺度按算子范数衡量以指数形式衰减,那么使用这个级数的第一项来近似梯度是有意义的。梯度的第一项来自于优化的最后一步,导致了一步梯度。
当Lh接近0时,很容易导致相对于h0的梯度消失,当Lh接近1时,很容易导致相对于x的梯度爆炸。此外,雅可比矩阵 @@yx 在Lh接近1时会出现病态条件的项(I −@@hF∗)−1,即@@Fh的最大特征值,即F相对于h的Lipschitz常数接近1,而其最小特征值通常接近0,从而限制了梯度在参数空间中搜索良好泛化解的能力。梯度通过优化算法反向传播的不规则尺度和频谱表明,直接将BPTT应用于Hamburger是不可行的,这在使用与第3.1节相同的消融设置的实验中得到了证实(见表1)。这种分析启发了我们一个可能的解决方案。需要注意的是,在BPTT算法中,存在多个雅可比矩阵的乘法 @hj @hj−@hj @hj−1 和无穷级数的求和,导致梯度的尺度无法控制。这启示我们在保留主导项的同时去除一些次要项,以确保梯度的方向大致正确。考虑将式(12)的项视为级数,即f@@hyt Qt j−=1t−i @@hhj+1 j @h@tx−i gi,如果其项的尺度按算子范数衡量以指数形式衰减,那么使用这个级数的第一项来近似梯度是有意义的。梯度的第一项来自于优化的最后一步,导致了一步梯度。 根据命题2,当t趋向于无穷大时,一步梯度是BPTT算法的线性近似。它很容易实现,只需要在PyTorch中进行no_grad操作(Paszke等,2019),或在TensorFlow中进行stop_gradient操作(Abadi等,2016),并将时间和空间复杂度从BPTT的O(t)降低到O(1)。我们测试了将更多的项添加到梯度中,但其性能比使用一步梯度要差。根据实验结果,一步梯度可以接受地通过MD进行梯度反向传播。
根据命题2,当t趋向于无穷大时,一步梯度是BPTT算法的线性近似。它很容易实现,只需要在PyTorch中进行no_grad操作(Paszke等,2019),或在TensorFlow中进行stop_gradient操作(Abadi等,2016),并将时间和空间复杂度从BPTT的O(t)降低到O(1)。我们测试了将更多的项添加到梯度中,但其性能比使用一步梯度要差。根据实验结果,一步梯度可以接受地通过MD进行梯度反向传播。
表2:对Hamburger的NMF Ham组件进行消融实验。
3.实验
在本节中,我们提供了实验结果,以展示上述技术的效果。我们选择了两个需要全局信息和注意机制的视觉任务进行实验,包括语义分割(超过50篇使用注意力的论文)和深度生成模型,如GAN(自注意力自SAGAN以来,大多数最先进的GAN都采用了自注意力)(Zhang等,2019a)。这两个任务具有很高的竞争性,足以用来比较Hamburger和自注意力。消融研究表明了Hamburger中MD的重要性以及一步梯度的必要性。我们强调Hamburger在建模全局上下文方面的优越性,无论是在性能还是在计算成本上。
3.1.消融实验
我们选择在PASCAL VOC数据集(Everingham等,2010)上进行所有消融实验,用于语义分割,并以最佳(均值)的形式报告验证集上5次运行的mIoU。对于所有消融实验,ResNet-50(He等,2016)是骨干网络,输出步幅为16。我们使用一个3×3的带有BN(Ioffe&Szegedy,2015)和ReLU的卷积层将通道数从2048减少到512,然后在与语义分割中常见的注意力位置添加Hamburger。有关详细的训练设置,请参见附录E.1。
 面包和火腿我们对Hamburger的每个部分进行消融实验。移除MD(ham)导致性能的严重下降,证明了MD的重要性。即使只添加了无参数的MD(只有ham),性能也可以明显提高。参数化还有助于Hamburger处理提取的特征。面包,特别是上层面包,对性能有相当大的贡献。
面包和火腿我们对Hamburger的每个部分进行消融实验。移除MD(ham)导致性能的严重下降,证明了MD的重要性。即使只添加了无参数的MD(只有ham),性能也可以明显提高。参数化还有助于Hamburger处理提取的特征。面包,特别是上层面包,对性能有相当大的贡献。
 值得注意的是,latent dimension(潜在维度)d和r之间的关系与mIoU测量的性能之间没有简单的线性关系,尽管d = 8r是一个令人满意的选择。实验证明,即使r = 8也表现良好,这表明对于建模全局上下文来说,它可能非常廉价。
值得注意的是,latent dimension(潜在维度)d和r之间的关系与mIoU测量的性能之间没有简单的线性关系,尽管d = 8r是一个令人满意的选择。实验证明,即使r = 8也表现良好,这表明对于建模全局上下文来说,它可能非常廉价。
3.2.仔细观察Hamburger
为了理解Hamburger在网络中的行为,我们在PASCAL VOC验证集上可视化了Hamburger之前和之后的表示的频谱。输入和输出张量被展开成RC×HW。在展开矩阵中,最大r个奇异值的平方之和与总奇异值的平方之和的累积比例在图5中显示。由于低秩重构,经典矩阵分解模型的结果通常观察到截断的频谱。在网络中,Hamburger也通过跳跃连接提升了能量的集中,同时保留了信息丰富的细节。另外,我们在图6中可视化了Hamburger之前和之后的特征图。MD通过将无信息的通道清零,去除不规则的噪声,并根据上下文完善细节,帮助Hamburger学习可解释的全局信息。
3.3.与注意力的比较
本节展示了基于MD的Hamburger在计算成本、内存消耗和推理时间方面相对于注意力相关的上下文模块的优势。我们将Hamburger(Ham)与自注意力(SA)(Vaswani等,2017)、DANet中的双注意力(DA)模块(Fu等,2019)、A2 Net中的双重注意力模块(Chen等,2018b)、APCNet中的APC模块(He等,2019b)、DMNet中的DM模块(He等,2019a)、CFNet中的ACF模块(Zhang等,2019b)进行比较,并在表3中报告了处理一个张量Z(大小为1×512×128×128)的参数和成本。在实际应用中,过多的内存使用是与注意力协作的关键瓶颈。因此,我们还提供了在NVIDIA TITAN Xp上的GPU负载和推理时间。总体而言,与注意力相关的全局上下文模块相比,Hamburger在计算和内存方面轻量级。
3.4.语义分割
我们在PASCAL VOC数据集(Everingham等,2010)和PASCAL Context数据集(Mottaghi等,2014)上对Hamburger进行了基准测试,并与最先进的注意力模型进行了比较。我们使用ResNet-101(He等,2016)作为我们的主干网络。主干网络的输出步幅为8。分割头与消融实验中的相同。在消融研究中,NMF通常比CD和VQ表现更好(参见表1)。因此,我们在后续实验中主要测试NMF。我们使用HamNet来表示带有Hamburger的ResNet。在PASCAL VOC测试集和PASCAL Context验证集上的结果分别在表4和表5中显示。我们将所有基于注意力的模型标记为∗,其中多样的注意力组成了分割头。尽管语义分割是一个饱和的任务,并且大多数现代发布的工作具有近似的性能,但Hamburger在以前的最先进的注意力模块上显示出了相当大的改进。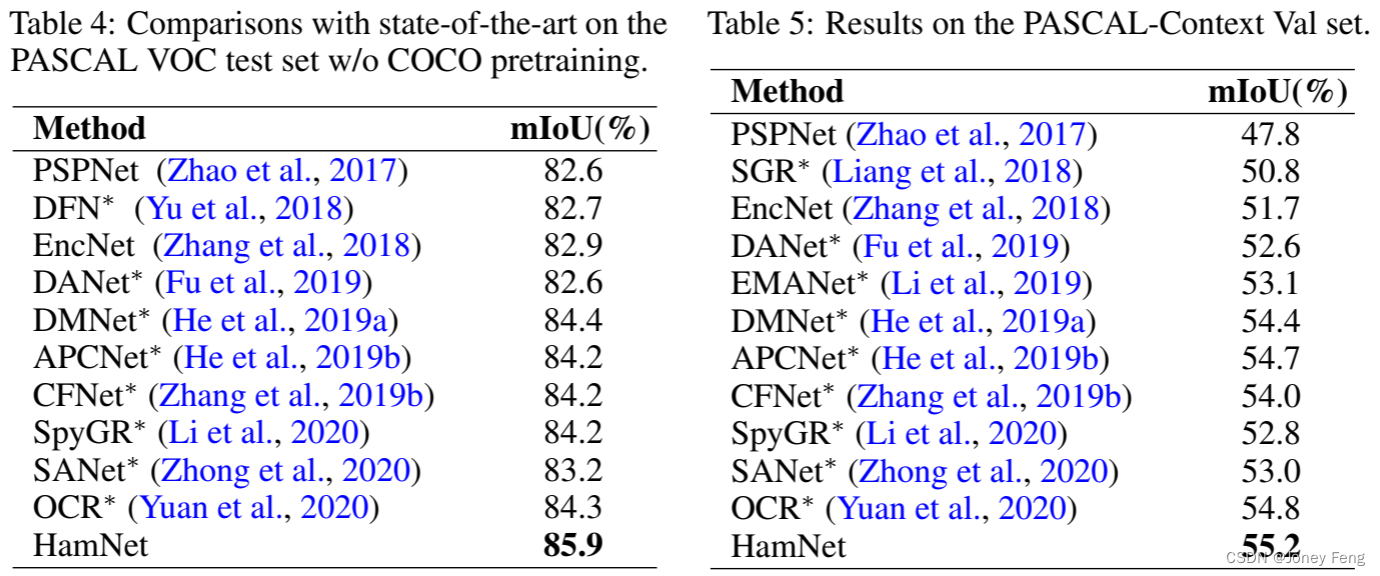
3.5.图像生成
在深度生成模型(如GANs)中,注意力作为全局上下文描述块存在。自从SAGAN(Zhang等,2019a)之后,大多数用于条件图像生成的最先进的GANs都将自注意力集成到它们的架构中,例如BigGAN(Brock等,2018)、S3GAN(Lucić等,2019)和LOGAN(Wu等,2019)。在具有挑战性的ImageNet(Deng等,2009)条件图像生成任务中,对基于MD的Hamburger进行基准测试是有说服力的。我们进行了实验,比较了Hamburger和自注意力在ImageNet 128×128上的表现。在特征分辨率为32×32的生成器和判别器中,自注意力被NMF Hamburger替代,命名为HamGAN-baby。HamGAN在Frechet Inception Distance(FID)(Heusel等,2017)上相对于SAGAN取得了可观的改善。此外,我们还使用最近开发的注意力变体Your Local GAN(YLG)(Daras等,2020)的代码库和相同的训练设置来比较Hamburger,命名为HamGAN-strong。HamGAN-strong在FID上提供了超过5%的改善,同时在总训练时间上快了15%,模块时间快了3.6倍(HamGAN的1.54 iters/sec,YLG的1.31 iters/sec,没有任何上下文模块的平均值为1.65 iters/sec,基于1000次迭代)。这些实验在相同的TPUv3训练平台上进行。

4.相关工作
在深度学习领域,过去五年见证了注意力机制(Bahdanau等,2015;Mnih等,2014;Xu等,2015;Luong等,2015)取得了巨大的成功。粗略地说,注意力机制是根据需求自适应地生成目标权重以进行关注。它的架构多种多样,其中最著名的是点积自注意力(Vaswani等,2017)。注意力机制有广泛的应用领域,从单一来源(Lin等,2017)到多源输入(Luong等,2015;Parikh等,2016),从全局信息发现(Wang等,2018;Zhang等,2019a)到局部特征提取(Dai等,2017;Parmar等,2019)。以往的研究人员尝试从多个方面解释注意力机制的有效性。捕捉长程依赖关系(Wang等,2018)、顺序分解视觉场景(Eslami等,2016;Kosiorek等,2018)、推断部分和整体之间的关系(Sabour等,2017;Hinton等,2018)、模拟对象之间的交互(Greff等,2017;van Steenkiste等,2018)以及学习环境的动态(Goyal等,2019)通常被认为是注意力的潜在机制。
从生物学角度来看,一个常见的观点是注意力模拟了许多无意识情境中的关注点的出现(Xu等,2015)。一些工作试图通过可视化或攻击注意力权重(Serrano和Smith,2019;Jain和Wallace,2019;Wiegreffe和Pinter,2019)来解释注意力机制,而其他人则将注意力形式化为非局部操作(Wang等,2018)或扩散模型(Tao等,2018;Lu等,2019),或者通过最大期望算法(Greff等,2017;Hinton等,2018;Li等,2019)或变分推断(Eslami等,2016)在混合模型上构建类似于注意力的模型。还讨论了Transformer和图神经网络之间的连接(Liang等,2018;Zhang等,2019c)。总体而言,关于注意力的讨论仍然远未达成一致意见或一致结论。
最近的研究通过低秩逼近在计算机视觉(Chen等,2018b;Zhu等,2019;Chen等,2019;Li等,2019)和自然语言处理(Mehta等,2019;Katharopoulos等,2020;Wang等,2020;Song等,2020)中开发了高效的注意力模块。从技术上讲,低秩逼近通常针对相关矩阵,即softmax操作后的Q和K的乘积,使用两个较小矩阵的乘积来逼近相关矩阵,并应用结合律来节省内存和计算成本,其中逼近涉及核函数或其他相似性函数。其他研究(Babiloni等,2020;Ma等,2019)努力将注意力形式化为张量形式,但可能会生成大型中间变量。本文不对注意力进行逼近或使其高效。本文将建模全局上下文视为低秩完成问题。计算和内存效率是对干净信号子空间的低秩假设和优化算法作为架构的副产品。
在深度学习中,矩阵分解与深度学习的结合有着悠久的历史。研究人员通过对权重进行因式分解来减少网络中的参数,包括softmax层(Sainath等,2013)、卷积层(Zhong等,2019)和嵌入层(Lan等,2019)。Tariyal等(2016)尝试构建深度字典学习用于特征提取,并通过贪婪训练模型。本文试图对表示进行因式分解,以恢复干净信号子空间作为全局上下文,并通过矩阵分解提供了一种建模长程依赖关系的新方法。
5.总结
本文研究了在网络中建模长程依赖关系。我们将学习全局上下文的过程形式化为一个低秩完成问题。受到低秩形式化的启发,我们基于广为研究的矩阵分解模型开发了Hamburger模块。通过特定的矩阵分解目标函数,其优化算法创建的计算图自然地定义了Hamburger的核心架构。Hamburger通过去噪和完成其输入来学习可解释的全局上下文,并改善谱的集中度。令人惊讶的是,当谨慎处理反向梯度时,即使是20年前提出的简单矩阵分解在具有挑战性的视觉任务(如语义分割和图像生成)中也能与自注意力一样强大,而且轻量、快速和内存高效。我们计划通过整合位置信息和设计类似Transformer的解码器,将Hamburger扩展到自然语言处理领域,为一步梯度技巧建立理论基础,或找到更好的区分矩阵分解的方法,并在未来整合先进的矩阵分解方法。
# -*- coding: utf-8 -*-
"""
Hamburger for Pytorch
@author: Gsunshine
"""
from functools import partial
import numpy as np
import settings
import torch
from sync_bn.nn.modules import SynchronizedBatchNorm2d
from torch import nn
from torch.nn import functional as F
from torch.nn.modules.batchnorm import _BatchNorm
norm_layer = partial(SynchronizedBatchNorm2d, momentum=settings.BN_MOM)
class ConvBNReLU(nn.Module):
@classmethod
def _same_paddings(cls, kernel_size):
if kernel_size == 1:
return 0
elif kernel_size == 3:
return 1
def __init__(self, in_c, out_c,
kernel_size=1, stride=1, padding='same',
dilation=1, groups=1):
super().__init__()
if padding == 'same':
padding = self._same_paddings(kernel_size)
self.conv = nn.Conv2d(in_c, out_c,
kernel_size=kernel_size, stride=stride,
padding=padding, dilation=dilation,
groups=groups,
bias=False)
self.bn = norm_layer(out_c)
self.act = nn.ReLU(inplace=True)
def forward(self, x):
x = self.conv(x)
x = self.bn(x)
x = self.act(x)
return x# -*- coding: utf-8 -*-
"""
Hamburger for Pytorch
@author: Gsunshine
"""
import numpy as np
import torch
from torch import nn
from torch.nn import functional as F
from torch.nn.modules.batchnorm import _BatchNorm
from .bread import ConvBNReLU, norm_layer
from .ham import get_hams
class HamburgerV1(nn.Module):
def __init__(self, in_c, args=None):
super().__init__()
ham_type = getattr(args, 'HAM_TYPE', 'NMF')
D = getattr(args, 'MD_D', 512)
if ham_type == 'NMF':
self.lower_bread = nn.Sequential(nn.Conv2d(in_c, D, 1),
nn.ReLU(inplace=True))
else:
self.lower_bread = nn.Conv2d(in_c, D, 1)
HAM = get_hams(ham_type)
self.ham = HAM(args)
self.upper_bread = nn.Sequential(nn.Conv2d(D, in_c, 1, bias=False),
norm_layer(in_c))
self.shortcut = nn.Sequential()
self._init_weight()
print('ham', HAM)
def _init_weight(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
N = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
m.weight.data.normal_(0, np.sqrt(2. / N))
elif isinstance(m, _BatchNorm):
m.weight.data.fill_(1)
if m.bias is not None:
m.bias.data.zero_()
def forward(self, x):
shortcut = self.shortcut(x)
x = self.lower_bread(x)
x = self.ham(x)
x = self.upper_bread(x)
x = F.relu(x + shortcut, inplace=True)
return x
def online_update(self, bases):
if hasattr(self.ham, 'online_update'):
self.ham.online_update(bases)
class HamburgerV2(nn.Module):
def __init__(self, in_c, args=None):
super().__init__()
ham_type = getattr(args, 'HAM_TYPE', 'NMF')
C = getattr(args, 'MD_D', 512)
if ham_type == 'NMF':
self.lower_bread = nn.Sequential(nn.Conv2d(in_c, C, 1),
nn.ReLU(inplace=True))
else:
self.lower_bread = nn.Conv2d(in_c, C, 1)
HAM = get_hams(ham_type)
self.ham = HAM(args)
self.cheese = ConvBNReLU(C, C)
self.upper_bread = nn.Conv2d(C, in_c, 1, bias=False)
self.shortcut = nn.Sequential()
self._init_weight()
print('ham', HAM)
def _init_weight(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
N = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
m.weight.data.normal_(0, np.sqrt(2. / N))
elif isinstance(m, _BatchNorm):
m.weight.data.fill_(1)
if m.bias is not None:
m.bias.data.zero_()
def forward(self, x):
shortcut = self.shortcut(x)
x = self.lower_bread(x)
x = self.ham(x)
x = self.cheese(x)
x = self.upper_bread(x)
x = F.relu(x + shortcut, inplace=True)
return x
def online_update(self, bases):
if hasattr(self.ham, 'online_update'):
self.ham.online_update(bases)
class HamburgerV2Plus(nn.Module):
def __init__(self, in_c, args=None):
super().__init__()
ham_type = getattr(args, 'HAM_TYPE', 'NMF')
S = getattr(args, 'MD_S', 1)
D = getattr(args, 'MD_D', 512)
C = S * D
self.dual = getattr(args, 'DUAL', True)
if self.dual:
C = 2 * C
if ham_type == 'NMF':
self.lower_bread = nn.Sequential(nn.Conv2d(in_c, C, 1),
nn.ReLU(inplace=True))
else:
self.lower_bread = nn.Conv2d(in_c, C, 1)
HAM = get_hams(ham_type)
if self.dual:
args.SPATIAL = True
self.ham_1 = HAM(args)
args.SPATIAL = False
self.ham_2 = HAM(args)
else:
self.ham = HAM(args)
factor = getattr(args, 'CHEESE_FACTOR', S)
if self.dual:
factor = 2 * factor
self.cheese = ConvBNReLU(C, C // factor)
self.upper_bread = nn.Conv2d(C // factor, in_c, 1, bias=False)
zero_ham = getattr(args, 'ZERO_HAM', True)
if zero_ham:
coef_ham_init = 0.
else:
coef_ham_init = 1.
self.coef_shortcut = nn.Parameter(torch.tensor([1.]))
self.coef_ham = nn.Parameter(torch.tensor([coef_ham_init]))
self.shortcut = nn.Sequential()
self._init_weight()
print('ham', HAM)
print('dual', self.dual)
def _init_weight(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
N = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
m.weight.data.normal_(0, np.sqrt(2. / N))
elif isinstance(m, _BatchNorm):
m.weight.data.fill_(1)
if m.bias is not None:
m.bias.data.zero_()
def forward(self, x):
shortcut = self.shortcut(x)
x = self.lower_bread(x)
if self.dual:
x = x.view(x.shape[0], 2, x.shape[1] // 2, *x.shape[2:])
x_1 = self.ham_1(x.narrow(1, 0, 1).squeeze(dim=1))
x_2 = self.ham_2(x.narrow(1, 1, 1).squeeze(dim=1))
x = torch.cat([x_1, x_2], dim=1)
else:
x = self.ham(x)
x = self.cheese(x)
x = self.upper_bread(x)
x = self.coef_ham * x + self.coef_shortcut * shortcut
x = F.relu(x, inplace=True)
return x
def online_update(self, bases):
if hasattr(self.ham, 'online_update'):
self.ham.online_update(bases)
def get_hamburger(version):
burgers = {'V1':HamburgerV1,
'V2':HamburgerV2,
'V2+': HamburgerV2Plus}
assert version in burgers
return burgers[version]# -*- coding: utf-8 -*-
"""
Hamburger for Pytorch
@author: Gsunshine
"""
import torch
from torch import nn
from torch.nn import functional as F
from torch.nn.modules.batchnorm import _BatchNorm
class _MatrixDecomposition2DBase(nn.Module):
def __init__(self, args):
super().__init__()
self.spatial = getattr(args, 'SPATIAL', True)
self.S = getattr(args, 'MD_S', 1)
self.D = getattr(args, 'MD_D', 512)
self.R = getattr(args, 'MD_R', 64)
self.train_steps = getattr(args, 'TRAIN_STEPS', 6)
self.eval_steps = getattr(args, 'EVAL_STEPS', 7)
self.inv_t = getattr(args, 'INV_T', 100)
self.eta = getattr(args, 'ETA', 0.9)
self.rand_init = getattr(args, 'RAND_INIT', True)
print('spatial', self.spatial)
print('S', self.S)
print('D', self.D)
print('R', self.R)
print('train_steps', self.train_steps)
print('eval_steps', self.eval_steps)
print('inv_t', self.inv_t)
print('eta', self.eta)
print('rand_init', self.rand_init)
def _build_bases(self, B, S, D, R, cuda=False):
raise NotImplementedError
def local_step(self, x, bases, coef):
raise NotImplementedError
@torch.no_grad()
def local_inference(self, x, bases):
# (B * S, D, N)^T @ (B * S, D, R) -> (B * S, N, R)
coef = torch.bmm(x.transpose(1, 2), bases)
coef = F.softmax(self.inv_t * coef, dim=-1)
steps = self.train_steps if self.training else self.eval_steps
for _ in range(steps):
bases, coef = self.local_step(x, bases, coef)
return bases, coef
def compute_coef(self, x, bases, coef):
raise NotImplementedError
def forward(self, x, return_bases=False):
B, C, H, W = x.shape
# (B, C, H, W) -> (B * S, D, N)
if self.spatial:
D = C // self.S
N = H * W
x = x.view(B * self.S, D, N)
else:
D = H * W
N = C // self.S
x = x.view(B * self.S, N, D).transpose(1, 2)
if not self.rand_init and not hasattr(self, 'bases'):
bases = self._build_bases(1, self.S, D, self.R, cuda=True)
self.register_buffer('bases', bases)
# (S, D, R) -> (B * S, D, R)
if self.rand_init:
bases = self._build_bases(B, self.S, D, self.R, cuda=True)
else:
bases = self.bases.repeat(B, 1, 1)
bases, coef = self.local_inference(x, bases)
# (B * S, N, R)
coef = self.compute_coef(x, bases, coef)
# (B * S, D, R) @ (B * S, N, R)^T -> (B * S, D, N)
x = torch.bmm(bases, coef.transpose(1, 2))
# (B * S, D, N) -> (B, C, H, W)
if self.spatial:
x = x.view(B, C, H, W)
else:
x = x.transpose(1, 2).view(B, C, H, W)
# (B * H, D, R) -> (B, H, N, D)
bases = bases.view(B, self.S, D, self.R)
if not self.rand_init and not self.training and not return_bases:
self.online_update(bases)
# if not self.rand_init or return_bases:
# return x, bases
# else:
return x
@torch.no_grad()
def online_update(self, bases):
# (B, S, D, R) -> (S, D, R)
update = bases.mean(dim=0)
self.bases += self.eta * (update - self.bases)
self.bases = F.normalize(self.bases, dim=1)
class VQ2D(_MatrixDecomposition2DBase):
def __init__(self, args):
super().__init__(args)
def _build_bases(self, B, S, D, R, cuda=False):
if cuda:
bases = torch.randn((B * S, D, R)).cuda()
else:
bases = torch.randn((B * S, D, R))
bases = F.normalize(bases, dim=1)
return bases
@torch.no_grad()
def local_step(self, x, bases, _):
# (B * S, D, N), normalize x along D (for cosine similarity)
std_x = F.normalize(x, dim=1)
# (B * S, D, R), normalize bases along D (for cosine similarity)
std_bases = F.normalize(bases, dim=1, eps=1e-6)
# (B * S, D, N)^T @ (B * S, D, R) -> (B * S, N, R)
coef = torch.bmm(std_x.transpose(1, 2), std_bases)
# softmax along R
coef = F.softmax(self.inv_t * coef, dim=-1)
# normalize along N
coef = coef / (1e-6 + coef.sum(dim=1, keepdim=True))
# (B * S, D, N) @ (B * S, N, R) -> (B * S, D, R)
bases = torch.bmm(x, coef)
return bases, coef
def compute_coef(self, x, bases, _):
with torch.no_grad():
# (B * S, D, N) -> (B * S, 1, N)
x_norm = x.norm(dim=1, keepdim=True)
# (B * S, D, N) / (B * S, 1, N) -> (B * S, D, N)
std_x = x / (1e-6 + x_norm)
# (B * S, D, R), normalize bases along D (for cosine similarity)
std_bases = F.normalize(bases, dim=1, eps=1e-6)
# (B * S, N, D)^T @ (B * S, D, R) -> (B * S, N, R)
coef = torch.bmm(std_x.transpose(1, 2), std_bases)
# softmax along R
coef = F.softmax(self.inv_t * coef, dim=-1)
return coef
class CD2D(_MatrixDecomposition2DBase):
def __init__(self, args):
super().__init__(args)
self.beta = getattr(args, 'BETA', 0.1)
print('beta', self.beta)
def _build_bases(self, B, S, D, R, cuda=False):
if cuda:
bases = torch.randn((B * S, D, R)).cuda()
else:
bases = torch.randn((B * S, D, R))
bases = F.normalize(bases, dim=1)
return bases
@torch.no_grad()
def local_step(self, x, bases, _):
# normalize x along D (for cosine similarity)
std_x = F.normalize(x, dim=1)
# (B * S, N, D) @ (B * S, D, R) -> (B * S, N, R)
coef = torch.bmm(std_x.transpose(1, 2), bases)
# softmax along R
coef = F.softmax(self.inv_t * coef, dim=-1)
# normalize along N
coef = coef / (1e-6 + coef.sum(dim=1, keepdim=True))
# (B * S, D, N) @ (B * S, N, R) -> (B * S, D, R)
bases = torch.bmm(x, coef)
# normalize along D
bases = F.normalize(bases, dim=1, eps=1e-6)
return bases, coef
def compute_coef(self, x, bases, _):
# [(B * S, R, D) @ (B * S, D, R) + (B * S, R, R)] ^ (-1) -> (B * S, R, R)
temp = torch.bmm(bases.transpose(1, 2), bases) \
+ self.beta * torch.eye(self.R).repeat(x.shape[0], 1, 1).cuda()
temp = torch.inverse(temp)
# (B * S, D, N)^T @ (B * S, D, R) @ (B * S, R, R) -> (B * S, N, R)
coef = x.transpose(1, 2).bmm(bases).bmm(temp)
return coef
class NMF2D(_MatrixDecomposition2DBase):
def __init__(self, args):
super().__init__(args)
self.inv_t = 1
def _build_bases(self, B, S, D, R, cuda=False):
if cuda:
bases = torch.rand((B * S, D, R)).cuda()
else:
bases = torch.rand((B * S, D, R))
bases = F.normalize(bases, dim=1)
return bases
@torch.no_grad()
def local_step(self, x, bases, coef):
# (B * S, D, N)^T @ (B * S, D, R) -> (B * S, N, R)
numerator = torch.bmm(x.transpose(1, 2), bases)
# (B * S, N, R) @ [(B * S, D, R)^T @ (B * S, D, R)] -> (B * S, N, R)
denominator = coef.bmm(bases.transpose(1, 2).bmm(bases))
# Multiplicative Update
coef = coef * numerator / (denominator + 1e-6)
# (B * S, D, N) @ (B * S, N, R) -> (B * S, D, R)
numerator = torch.bmm(x, coef)
# (B * S, D, R) @ [(B * S, N, R)^T @ (B * S, N, R)] -> (B * S, D, R)
denominator = bases.bmm(coef.transpose(1, 2).bmm(coef))
# Multiplicative Update
bases = bases * numerator / (denominator + 1e-6)
return bases, coef
def compute_coef(self, x, bases, coef):
# (B * S, D, N)^T @ (B * S, D, R) -> (B * S, N, R)
numerator = torch.bmm(x.transpose(1, 2), bases)
# (B * S, N, R) @ (B * S, D, R)^T @ (B * S, D, R) -> (B * S, N, R)
denominator = coef.bmm(bases.transpose(1, 2).bmm(bases))
# multiplication update
coef = coef * numerator / (denominator + 1e-6)
return coef
def get_hams(key):
hams = {'VQ':VQ2D,
'CD':CD2D,
'NMF':NMF2D}
assert key in hams
return hams[key]import math
import os.path as osp
from functools import partial
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.nn.modules.batchnorm import _BatchNorm
import settings
from hamburger import ConvBNReLU, get_hamburger
from sync_bn.nn.modules import SynchronizedBatchNorm2d
norm_layer = partial(SynchronizedBatchNorm2d, momentum=settings.BN_MOM)
class Bottleneck(nn.Module):
expansion = 4
def __init__(self, inplanes, planes, stride=1, dilation=1,
downsample=None, previous_dilation=1):
super().__init__()
self.conv1 = nn.Conv2d(inplanes, planes, 1, bias=False)
self.bn1 = norm_layer(planes)
self.conv2 = nn.Conv2d(planes, planes, 3, stride, dilation, dilation,
bias=False)
self.bn2 = norm_layer(planes)
self.conv3 = nn.Conv2d(planes, planes * 4, 1, bias=False)
self.bn3 = norm_layer(planes * 4)
self.relu = nn.ReLU(inplace=True)
self.downsample = downsample
self.dilation = dilation
self.stride = stride
def forward(self, x):
residual = x
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
out = self.relu(out)
out = self.conv3(out)
out = self.bn3(out)
if self.downsample is not None:
residual = self.downsample(x)
out += residual
out = self.relu(out)
return out
class ResNet(nn.Module):
def __init__(self, block, layers, num_classes=1000, stride=8):
self.inplanes = 128
super().__init__()
self.conv1 = nn.Sequential(
nn.Conv2d(3, 64, kernel_size=3, stride=2, padding=1, bias=False),
norm_layer(64),
nn.ReLU(inplace=True),
nn.Conv2d(64, 64, kernel_size=3, stride=1, padding=1, bias=False),
norm_layer(64),
nn.ReLU(inplace=True),
nn.Conv2d(64, 128, kernel_size=3, stride=1, padding=1, bias=False))
self.bn1 = norm_layer(self.inplanes)
self.relu = nn.ReLU(inplace=True)
self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
self.layer1 = self._make_layer(block, 64, layers[0])
self.layer2 = self._make_layer(block, 128, layers[1], stride=2)
if stride == 16:
self.layer3 = self._make_layer(block, 256, layers[2], stride=2)
self.layer4 = self._make_layer(
block, 512, layers[3], stride=1, dilation=2, grids=[1,2,4])
elif stride == 8:
self.layer3 = self._make_layer(
block, 256, layers[2], stride=1, dilation=2)
self.layer4 = self._make_layer(
block, 512, layers[3], stride=1, dilation=4, grids=[1,2,4])
self.avgpool = nn.AvgPool2d(7, stride=1)
self.fc = nn.Linear(512 * block.expansion, num_classes)
for m in self.modules():
if isinstance(m, nn.Conv2d):
n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
m.weight.data.normal_(0, math.sqrt(2. / n))
elif isinstance(m, _BatchNorm):
m.weight.data.fill_(1)
if m.bias is not None:
m.bias.data.zero_()
def _make_layer(self, block, planes, blocks, stride=1, dilation=1,
grids=None):
downsample = None
if stride != 1 or self.inplanes != planes * block.expansion:
downsample = nn.Sequential(
nn.Conv2d(self.inplanes, planes * block.expansion,
kernel_size=1, stride=stride, bias=False),
norm_layer(planes * block.expansion))
layers = []
if grids is None:
grids = [1] * blocks
if dilation == 1 or dilation == 2:
layers.append(block(self.inplanes, planes, stride, dilation=1,
downsample=downsample,
previous_dilation=dilation))
elif dilation == 4:
layers.append(block(self.inplanes, planes, stride, dilation=2,
downsample=downsample,
previous_dilation=dilation))
else:
raise RuntimeError('=> unknown dilation size: {}'.format(dilation))
self.inplanes = planes * block.expansion
for i in range(1, blocks):
layers.append(block(self.inplanes, planes,
dilation=dilation*grids[i],
previous_dilation=dilation))
return nn.Sequential(*layers)
def forward(self, x):
x = self.conv1(x)
x = self.bn1(x)
x = self.relu(x)
x = self.maxpool(x)
x = self.layer1(x)
x = self.layer2(x)
x = self.layer3(x)
x = self.layer4(x)
x = self.avgpool(x)
x = x.view(x.size(0), -1)
x = self.fc(x)
return x
def resnet(n_layers, stride):
layers = {
50: [3, 4, 6, 3],
101: [3, 4, 23, 3],
152: [3, 8, 36, 3],
}[n_layers]
pretrained_path = {
50: osp.join(settings.MODEL_DIR, 'resnet50-ebb6acbb.pth'),
101: osp.join(settings.MODEL_DIR, 'resnet101-2a57e44d.pth'),
152: osp.join(settings.MODEL_DIR, 'resnet152-0d43d698.pth'),
}[n_layers]
net = ResNet(Bottleneck, layers=layers, stride=stride)
state_dict = torch.load(pretrained_path)
net.load_state_dict(state_dict, strict=False)
return net
class CrossEntropyLoss2d(nn.Module):
def __init__(self, weight=None, reduction='none', ignore_index=-1):
super(CrossEntropyLoss2d, self).__init__()
self.nll_loss = nn.NLLLoss(weight, reduction=reduction,
ignore_index=ignore_index)
def forward(self, inputs, targets):
loss = self.nll_loss(F.log_softmax(inputs, dim=1), targets)
return loss.mean(dim=2).mean(dim=1)
class HamNet(nn.Module):
def __init__(self, n_classes, n_layers):
super().__init__()
backbone = resnet(n_layers, settings.STRIDE)
self.backbone = nn.Sequential(
backbone.conv1,
backbone.bn1,
backbone.relu,
backbone.maxpool,
backbone.layer1,
backbone.layer2,
backbone.layer3,
backbone.layer4)
C = settings.CHANNELS
self.squeeze = ConvBNReLU(2048, C, 3)
Hamburger = get_hamburger(settings.VERSION)
self.hamburger = Hamburger(C, settings)
self.align = ConvBNReLU(C, 256, 3)
self.fc = nn.Sequential(nn.Dropout2d(p=0.1),
nn.Conv2d(256, n_classes, 1))
# Put the criterion inside the model to make GPU load balanced
self.crit = CrossEntropyLoss2d(ignore_index=settings.IGNORE_LABEL,
reduction='none')
def forward(self, img, lbl=None, size=None):
x = self.backbone(img)
x = self.squeeze(x)
x = self.hamburger(x)
x = self.align(x)
x = self.fc(x)
if size is None:
size = img.size()[-2:]
pred = F.interpolate(x, size=size, mode='bilinear', align_corners=True)
if self.training and lbl is not None:
loss = self.crit(pred, lbl)
return loss
else:
return pred
def test_net():
model = HamNet(n_classes=21, n_layers=50)
model.eval()
print(list(model.named_children()))
image = torch.randn(1, 3, 513, 513)
label = torch.zeros(1, 513, 513).long()
pred = model(image, label)
print(pred.size())
if __name__ == '__main__':
test_net()






![[linux] SFTP文件传输基本命令 --- xshell 直接上传文件](https://img-blog.csdnimg.cn/1e168d7d1f3a443e9eba3c9f3b054397.png)