深度之眼官方账号 - 01-04-mp4-计算图与动态图机制
前置知识:计算图
可以参考我的笔记:
【学习笔记】计算机视觉与深度学习(2.全连接神经网络)
计算图
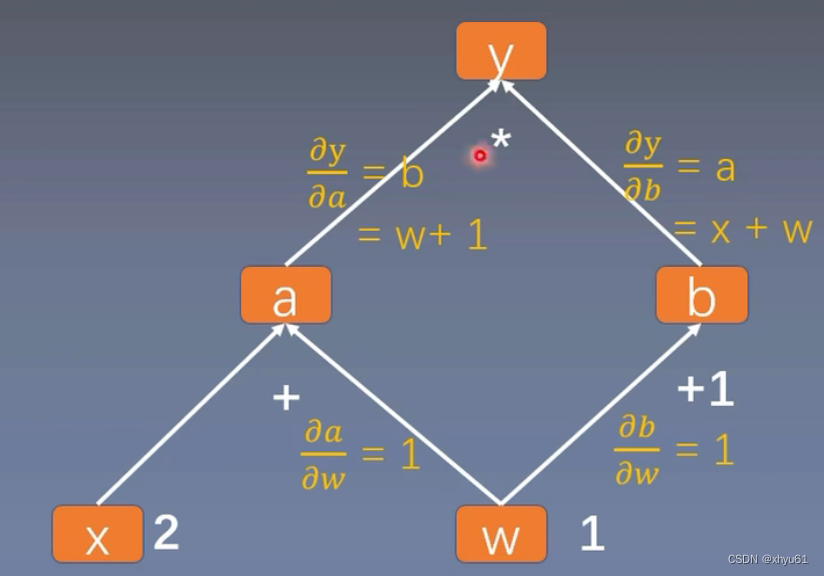
以这棵计算图为例。这个计算图中,叶子节点为x和w。
import torch
w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)
# 调用backward()方法,开始反向求梯度
y.backward()
print(w.grad)
print("is_leaf:\n", w.is_leaf, x.is_leaf, a.is_leaf, b.is_leaf, y.is_leaf)
print("gradient:\n", w.grad, x.grad, a.grad, b.grad, y.grad)
输出:
tensor([5.])
is_leaf:
True True False False False
gradient:
tensor([5.]) tensor([2.]) None None None
由此可见,非叶子节点在最后不会被保留梯度。这是出于节省空间的需要而这样设计的。实际的计算图会非常大,如果每个节点都保留梯度,会占用非常大的存储空间,而这些节点的梯度对于我们学习并没有什么帮助。
如果非要看他们的梯度,可以这样操作:在a = torch.add(w, x)的后面加上一句a.retain_grad(),这样a的梯度就会被存储起来。
输出会变成:
tensor([5.])
is_leaf:
True True False False False
gradient:
tensor([5.]) tensor([2.]) tensor([2.]) None None
对于节点,还可以看这些节点进行的运算。grad_fn,gradient function的缩写,表示这个节点的tensor是什么运算产生的。加一句:
print("gradient function:\n", w.grad_fn, '\n', x.grad_fn, '\n', a.grad_fn, '\n', b.grad_fn, '\n', y.grad_fn)
会输出
gradient function:
None
None
<AddBackward0 object at 0x000001B1DA3651C0>
<AddBackward0 object at 0x000001B1DA3651F0>
<MulBackward0 object at 0x000001B1DA3515B0>
retain_graph
import torch
w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
a = torch.add(w, x)
a.retain_grad()
b = torch.add(w, 1)
y = torch.mul(a, b)
# 调用backward()方法,开始反向求梯度
y.backward()
y.backward()
连续两次调用backward()方法,会报这样的错误:
RuntimeError: Trying to backward through the graph a second time (or directly access saved tensors after they have already been freed). Saved intermediate values of the graph are freed when you call .backward() or autograd.grad(). Specify retain_graph=True if you need to backward through the graph a second time or if you need to access saved tensors after calling backward.
原因是我们进行第一次backward()后,计算图就被自动释放掉了,进行第二次backward()时,没有计算图可以计算梯度,于是报错。
解决方案:backward内部添加一个参数:retain_graph=True,意思是计算完梯度后保留计算图。
# 调用backward()方法,开始反向求梯度
y.backward(retain_graph=True)
y.backward()
这样就不会报错了。
gradient
当计算图末部的节点有1个以上时,有时我们会希望他们之间的梯度有一个权重关系。这时就会用上gradient。
import torch
w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
a = torch.add(w, x)
b = torch.add(w, 1)
# 不难看出,y0和y1是两个互不干扰的末部节点
y0 = torch.mul(a, b)
y1 = torch.add(a, b)
# 将两个末部节点打包起来
loss = torch.cat([y0, y1], dim=0)
grad_tensors = torch.tensor([1., 2.])
# 将grad_tensors中的内容作为权重,变成y0+2y1
loss.backward(gradient=grad_tensors)
print(w.grad)
输出
tensor([9.])
如果把grad_tensors改成:
grad_tensors = torch.tensor([1., 3.])
输出变成:
tensor([11.])
torch.autograd.grad()
除了加减乘除法,我们还可以对torch进行求导操作。求的是 d ( o u t p u t s ) d ( i n p u t s ) \frac{d(outputs)}{d(inputs)} d(inputs)d(outputs)。
torch.autograd.grad(outputs,
inputs,
grad_outputs=None,
retain_graph=None,
create_graph=False)
outputs和inputs已在上述定义中给出;
grad_outputs:多梯度权重;
retain_graph:保留计算图;
create_graph:创建计算图。
import torch
# y = x ** 2
x = torch.tensor([3.], requires_grad=True)
y = torch.pow(x, 2)
# grad_1 = dy / dx = 2x = 6
grad_1 = torch.autograd.grad(y, x, create_graph=True)
print(grad_1)
# grad_2 = d(dy / dx) / dx = 2
grad_2 = torch.autograd.grad(grad_1, x)
print(grad_2)
输出
(tensor([6.], grad_fn=<MulBackward0>),)
(tensor([2.]),)
autograd注意事项
1.梯度不会自动清零
import torch
w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
for i in range(4):
a = torch.add(w, x)
b = torch.mul(w, x)
y = torch.mul(a, b)
y.backward()
print("w's grad: ", w.grad)
# w.grad.zero_()
输出:
w's grad: tensor([8.])
w's grad: tensor([16.])
w's grad: tensor([24.])
w's grad: tensor([32.])
由此可以看出,在不加上注释掉的那一行时,梯度在w处是不断累积的。而如果我们把print后面的那句w.grad.zero_()加上,输出就会变成:
w's grad: tensor([8.])
w's grad: tensor([8.])
w's grad: tensor([8.])
w's grad: tensor([8.])
w.grad.zero_()的意思就是把w处积累的梯度清零。
2.依赖于叶子节点的节点,requires_grad默认为True
可以从上面的代码中发现,我们只有在定义w和x两个tensor时,设置requires_grad为True。这个参数在定义tensor时默认为False。后面我们的a、b、y都没有设置这个参数。
如果我们定义w和x的时候不加上requires_grad=True,那么y.backward()这一步就会报错,因为我们的预设,这两个tensor不需要梯度,于是就无法求梯度。而w和x是我们计算图上的叶子节点,所以必须加上requires_grad=True。
而后面通过w和x延伸定义出的a、b、y,由于依赖的w、x的requires_grad是True,那么a、b、y的这个参数也被默认设置为了True,不需要我们手动添加。
3.叶子节点不可执行in-place操作
计算图上叶子节点处的tensor不能进行原地修改。
什么是in-place操作?
t = torch.tensor([1., 2.])
t.add_(3.)
print(t)
输出
tensor([4., 5.])
torch.Tensor.add_就是torch.add的in-place版本。所谓in-place,就是在tensor上进行原地修改。大部分的torch.tensor的运算,名字后面加一个下划线,就变成inplace操作了。
再比如求绝对值:
t = torch.tensor([-1., -2.])
t.abs_()
print(t)
输出
tensor([1., 2.])
知道什么是in-place操作后,我们尝试一下在requires_grad=True的叶子节点上原地修改,代码如下:
import torch
w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
a = torch.add(w, x)
b = torch.mul(w, x)
y = torch.mul(a, b)
w.add_(1)
y.backward()
报错信息:
RuntimeError: a leaf Variable that requires grad is being used in an in-place operation.