【SLAM数学基础】李群与李代数 BCH近似公式

news2025/1/15 21:00:21

三维旋转构成了三维旋转群 SO(3)，其对应的李代数为 $\mathfrak{so}$ (3)；三维变换构成了三维变换群 SE(3)，其对应的李代数为 $\mathfrak{se}$ (3)。

1.指数映射

李代数元素到李群元素的映射为指数映射，其中 $\mathfrak{so}$ (3) 至 SO(3) 的指数映射为：

$\exp(\bm{\phi}^{\wedge}) = \bm{R} = \text{Exp}(\bm{\phi})$

具体计算公式由罗德里格斯公式给出：

$\bm{R} = \cos\theta \cdot \bm{I} + (1-\cos \theta) \bm{n}\bm{n}^T + \sin\theta\cdot \bm{n}^{\wedge} = \exp(\bm{\phi}^{\wedge})$

其中 $\bm{\phi}\in \mathfrak{so}(3)$ 可以分解为 $\bm{\phi} =\theta\bm{n}$ .

2.对数映射

从李群元素到李代数元素的映射为对数映射，记作

$\bm{\phi} = \log(\bm{R})^{\vee} = \text{Log}(\bm{R})$

其中 $\bm{\phi}\in \mathfrak{so}(3)$ 可以分解为 $\bm{\phi} =\theta\bm{n}$ ，具体的计算过程由下式给出：

$\theta = \arccos\left(\frac{tr(\bm{R}) - 1}{2}\right) \\ \bm{R}\bm{n} = \bm{n}$

其中转轴 $\bm{n}$ 是矩阵 $R$ 特征值1对应的单位特征向量。

3. BCH公式及其线性近似表达

两个李代数指数映射乘积的完整形式，由 Baker-Campbell-Hausdorff 公式（BCH公式）给出，其展开式的前几项为：

$\ln\left(\exp(A)\exp(B)\right) = A + B + \frac{1}{2}[A, B] + \frac{1}{12}[A,[A,B]] - \frac{1}{12}[B,[A,B]] + \cdots$

其中 [ ] 为李括号。特别地，考虑 SO(3) 上的李代数 $\ln\left(\exp(\bm{\phi}^{\wedge}_1)\exp(\bm{\phi}^{\wedge}_2)\right)^{\vee}$ ，当 $\bm{\phi}_1$ 或 $\bm{\phi}_2$ 为小量时，小量二次以上的项可以忽略，此时 BCH 具有线性近似表达：

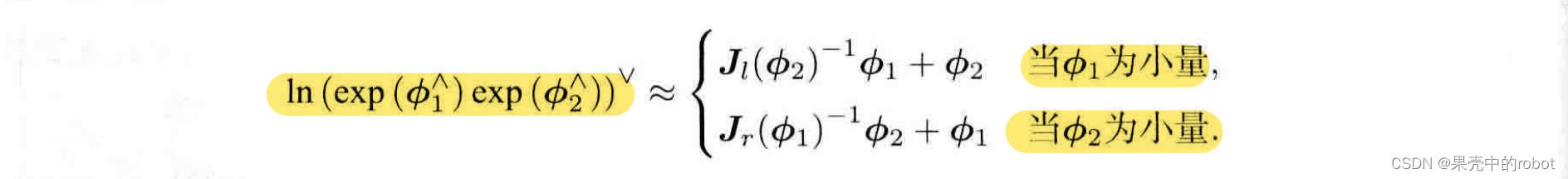
在这里插入图片描述

第一个近似公式表明，当对一个旋转矩阵 $\bm{R}_2$ (李代数为 $\bm{\phi}_2$ ) 左乘一个微小旋转矩阵 $\bm{R}_1$ (李代数为 $\bm{\phi}_1$ )时，可以近似看作在原来的李代数 $\bm{\phi}_2$ 加上了一项 $\bm{J}_l(\bm{\phi}_2)^{-1}\bm{\phi}_1$ 。同理，第二个近似公式描述了右乘一个微小旋转的情况。

因此，李代数在BCH近似下分成了左乘和右乘近似两种，使用时需要注意区分。

4. SO(3)上的BCH近似公式

BCH公式给出了李代数上的小量加法与李群上小量乘法之间的关系（李代数加法 $\Leftrightarrow$ 李群乘法），其线性近似公式广泛应用于各种函数的线性化。

在SO(3)中，某个旋转 $\bm{R}$ 对应的李代数为 $\bm{\phi}$ ，左乘一个微小旋转，记作 $\Delta \bm{R}$ ，对应的李代数为 $\Delta \bm{\phi}$ ，那么在李群上得到的结果就是 $\Delta \bm{R} \bm{R}$ ，而在李代数上，根据BCH近似，为 $\bm{J}_l(\bm{\phi})^{-1}\Delta\bm{\phi} + \bm{\phi}$ ，合并后可以简单写成：

$\Delta \bm{R} \bm{R} = \exp(\Delta \bm{\phi}^{\wedge})\exp(\bm{\phi}^{\wedge}) = \exp \left( (\bm{\phi} + \bm{J}_l(\bm{\phi})^{-1}\Delta\bm{\phi})^{\wedge} \right)$

反过来，如果在李代数上进行加法，让一个 $\bm{\phi}$ 加上小量 $\Delta \bm{\phi}$ ，那么可以近似为李群上带左右雅克比矩阵的乘法：

$\exp((\bm{\phi} + \Delta \bm{\phi})^{\wedge}) = \exp((\bm{J}_l(\bm{\phi})\Delta \bm{\phi})^\wedge) \exp(\bm{\phi}^\wedge) = \exp( \bm{\phi}^\wedge) \exp((\bm{J}_r(\bm{\phi})\Delta\bm{\phi})^\wedge)$

其中SO(3)的左雅克比矩阵为

$\bm{J}_l(\theta\bm{a}) = \frac{\sin\theta}{\theta} \bm{I} + (1-\frac{\sin\theta}{\theta})\bm{a}\bm{a}^T+(\frac{1-\cos\theta}{\theta})\bm{a}^{\wedge} \\ \bm{J}^{-1}_l(\theta\bm{a}) = \frac{\theta}{2}\cot\frac{\theta}{2} \bm{I} + (1-\frac{\theta}{2}\cot\frac{\theta}{2})\bm{a}\bm{a}^T-\frac{\theta}{2}\bm{a}^{\wedge}$

而SO(3)的右雅克比矩阵为

$\bm{J}_r(\bm{\phi}) = \bm{J}_l(-\bm{\phi})$

值得注意的是，由于李代数 $\bm{\phi}$ 可以和旋转矩阵 $\bm{R}$ 简单地对应起来，因此有时也把 $\bm{J}_r(\bm{\phi})$ 简单地记作 $\bm{J}_r(\bm{R})$ 而不是 $\bm{J}_r(\text{Log}(\bm{R}))$ 。另外，在很多情况下，也会省略 $\bm{J}_r(\bm{\phi})$ 括号里的内容，而直接记为 $\bm{J}_r$ 和 $\bm{J}_l$ ，这都是为了让公式看上去更加简洁。