💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
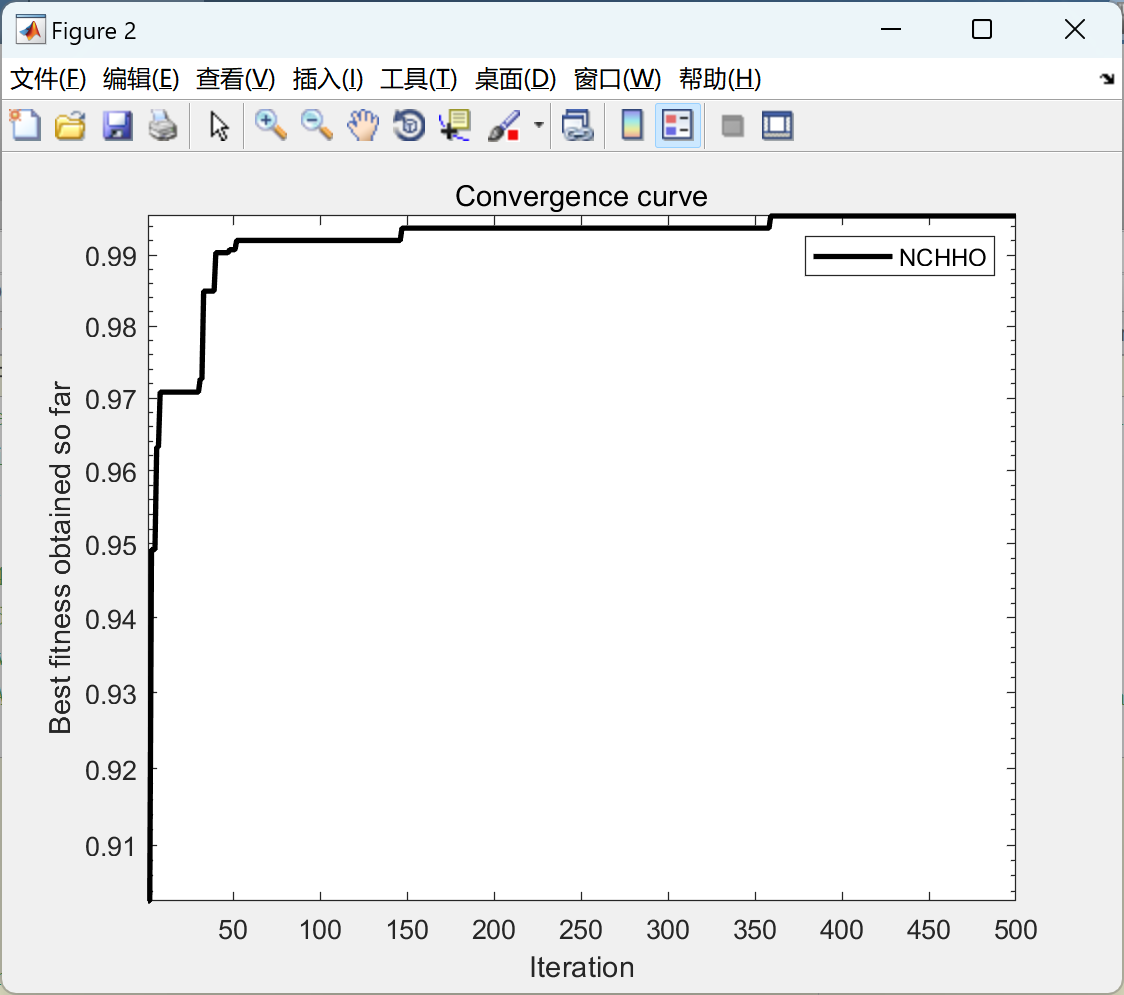
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码及文献
💥1 概述
Harris Hawks Optimizer (HHO) 是元启发式领域的众多最新算法之一。HHO算法模仿哈里斯鹰的合作行为及其在自然界中的觅食行为,称为惊喜突袭。HHO受益于少量的控制参数设置,实施的简单性以及高水平的勘探和开发。为了缓解该算法的缺点,该文提出一种基于非线性的混沌哈里斯鹰优化(NCHHO)的改进版本。NCHHO使用混沌和非线性控制参数来提高HHO的优化性能。在所提出的方法中使用混沌地图的主要目的是改善HHO的探索行为。此外,本文还引入了一个非线性控制参数来调整HHO的探索和开发行为。所提出的NCHHO算法使用各种混沌图展示了性能的改进,这些混沌图是为了识别最有效的混沌图,并在几个众所周知的基准函数上进行了测试。本文还考虑解决车联网(IoV)优化问题,该问题展示了NCHHO在解决大规模现实问题方面的适用性。结果表明,与其他算法相比,NCHHO算法非常具有竞争力,并且通常更胜一筹。特别是,NCHHO在求解问题维数为D = 92和30的单模态和多模态函数时,平均提供了50%更好的结果,而对于更高维的问题,我们提出的算法与其他算法相比,在D = 100和100的情况下显示出1000%一致的改进。在解决车联网问题时,成功率为62.5%,与最先进的算法相比,这要好得多。为此,本文提出的NCHHO算法展示了一种被不同应用广泛使用的有前途的方法,这为行业和企业解决日常遇到的优化问题带来了好处,例如资源分配,信息检索,寻找通过网络发送数据的最佳路径,路径规划以及许多其他应用。
【改进哈里鹰算法(NCHHO)】是一种使用混沌和非线性控制参数来提高哈里鹰算法优化性能的方法,用于解决与车联网相关的路由问题。
NCHHO方法通过引入混沌地图和非线性控制参数来改进HHO算法的性能。其中,混沌地图的应用旨在改善HHO算法的搜索行为,增强其对解空间的探索能力。此外,还引入了非线性控制参数来调节HHO算法的探索性和剥削性行为,使其具备更好的适应性和灵活性。
在该研究中,NCHHO算法通过采用多个混沌地图,并在多个众所周知的基准函数上进行测试,展示了性能的改进。通过比较不同混沌地图的效果,研究者能够确定最有效的混沌地图,并对算法进行优化。此外,该方法还考虑了解决车联网(IoV)优化问题,展示了NCHHO在解决大规模现实问题上的适用性和有效性。
这项研究为改进哈里鹰算法提供了一种新的方法,通过引入混沌和非线性控制参数,显著提高了算法的性能和适应性。通过在车联网路由问题中的应用,研究者们展示了NCHHO算法在实际场景下解决问题的能力。这对于提升车联网系统的路由效果和优化性能具有重要意义。

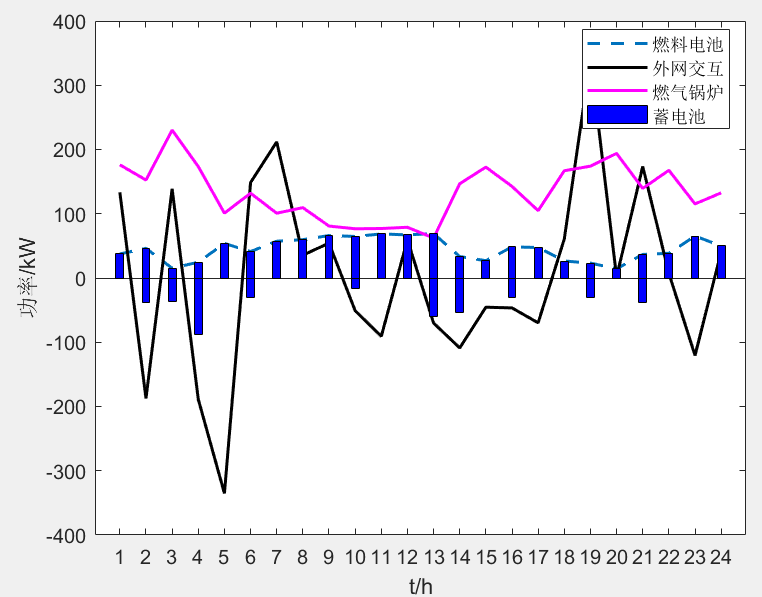
📚2 运行结果

部分代码:
function [Rabbit_Energy,Rabbit_Location,CNVG] = NCHHO_IoV(N,T,lb,ub,dim,fobj)
% initialize the location and Energy of the rabbit
Rabbit_Location=zeros(1,dim);
Rabbit_Energy=0;
%Initialize the locations of Harris' hawks
X=initialization(N,dim,ub,lb);
CNVG=zeros(1,T);
t=0; % Loop counter
while t<T
for i=1:size(X,1)
% Check boundries
FU=X(i,:)>ub;FL=X(i,:)<lb;X(i,:)=(X(i,:).*(~(FU+FL)))+ub.*FU+lb.*FL;
% fitness of locations
fitness=fobj(X(i,:));
% Update the location of Rabbit
if fitness>Rabbit_Energy
Rabbit_Energy=fitness;
Rabbit_Location=X(i,:);
end
end
E1=abs(2*(1-(t/T))-2); % factor to show the decreaing energy of rabbit
a1 = 4; % Initial chaotic map parameter configuration
teta = 0.7; % Initial chaotic map parameter configuration
% Update the location of Harris' hawks
for i=1:size(X,1)
for ii=1:4
Cm(1,ii) = abs((a1/4)*sin(pi*teta));
teta = Cm(1,ii);
end
E0=2*rand()-1; %-1<E0<1
Escaping_Energy=E1*(E0); % escaping energy of rabbit
if abs(Escaping_Energy)>=1
%% Exploration:
% Harris' hawks perch randomly based on 2 strategy:
q=rand();
rand_Hawk_index = floor(N*rand()+1);
X_rand = X(rand_Hawk_index, :);
if q<0.5
% perch based on other family members
X(i,:)=X_rand-Cm(1,1)*abs(X_rand-2*Cm(1,2)*X(i,:));
elseif q>=0.5
% perch on a random tall tree (random site inside group's home range)
X(i,:)=(Rabbit_Location(1,:)-mean(X))-Cm(1,3)*((ub-lb)*Cm(1,4)+lb);
end
elseif abs(Escaping_Energy)<1
%% Exploitation:
% Attacking the rabbit using 4 strategies regarding the behavior of the rabbit
%% phase 1: surprise pounce (seven kills)
% surprise pounce (seven kills): multiple, short rapid dives by different hawks
r=rand(); % probablity of each event
if r>=0.5 && abs(Escaping_Energy)<0.5 % Hard besiege
X(i,:)=(Rabbit_Location)-Escaping_Energy*abs(Rabbit_Location-X(i,:));
end
if r>=0.5 && abs(Escaping_Energy)>=0.5 % Soft besiege
Jump_strength=2*(1-rand()); % random jump strength of the rabbit
X(i,:)=(Rabbit_Location-X(i,:))-Escaping_Energy*abs(Jump_strength*Rabbit_Location-X(i,:));
end
%% phase 2: performing team rapid dives (leapfrog movements)
if r<0.5 && abs(Escaping_Energy)>=0.5 % Soft besiege % rabbit try to escape by many zigzag deceptive motions
w1=2*exp(-(8*t/T)^2); % Non-linear control Parameter
Jump_strength=2*(1-rand());
X1=w1*Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-X(i,:));
if fobj(X1)>fobj(X(i,:)) % improved move?
X(i,:)=X1;
else % hawks perform levy-based short rapid dives around the rabbit
X2=w1*Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-X(i,:))+rand(1,dim).*Levy(dim);
if (fobj(X2)>fobj(X(i,:))) % improved move?
X(i,:)=X2;
end
end
end
if r<0.5 && abs(Escaping_Energy)<0.5 % Hard besiege % rabbit try to escape by many zigzag deceptive motions
% hawks try to decrease their average location with the rabbit
w1=2*exp(-(8*t/T)^2);
Jump_strength=2*(1-rand());
X1=w1*Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-mean(X));
if fobj(X1)>fobj(X(i,:)) % improved move?
X(i,:)=X1;
else % Perform levy-based short rapid dives around the rabbit
X2=w1*Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-mean(X))+rand(1,dim).*Levy(dim);
if (fobj(X2)>fobj(X(i,:))) % improved move?
X(i,:)=X2;
end
end
end
%%
end
end
t=t+1;
CNVG(t)=Rabbit_Energy;
end
endfunction [Rabbit_Energy,Rabbit_Location,CNVG] = NCHHO_IoV(N,T,lb,ub,dim,fobj)
% initialize the location and Energy of the rabbit
Rabbit_Location=zeros(1,dim);
Rabbit_Energy=0;
%Initialize the locations of Harris' hawks
X=initialization(N,dim,ub,lb);
CNVG=zeros(1,T);
t=0; % Loop counter
while t<T
for i=1:size(X,1)
% Check boundries
FU=X(i,:)>ub;FL=X(i,:)<lb;X(i,:)=(X(i,:).*(~(FU+FL)))+ub.*FU+lb.*FL;
% fitness of locations
fitness=fobj(X(i,:));
% Update the location of Rabbit
if fitness>Rabbit_Energy
Rabbit_Energy=fitness;
Rabbit_Location=X(i,:);
end
end
E1=abs(2*(1-(t/T))-2); % factor to show the decreaing energy of rabbit
a1 = 4; % Initial chaotic map parameter configuration
teta = 0.7; % Initial chaotic map parameter configuration
% Update the location of Harris' hawks
for i=1:size(X,1)
for ii=1:4
Cm(1,ii) = abs((a1/4)*sin(pi*teta));
teta = Cm(1,ii);
end
E0=2*rand()-1; %-1<E0<1
Escaping_Energy=E1*(E0); % escaping energy of rabbit
if abs(Escaping_Energy)>=1
%% Exploration:
% Harris' hawks perch randomly based on 2 strategy:
q=rand();
rand_Hawk_index = floor(N*rand()+1);
X_rand = X(rand_Hawk_index, :);
if q<0.5
% perch based on other family members
X(i,:)=X_rand-Cm(1,1)*abs(X_rand-2*Cm(1,2)*X(i,:));
elseif q>=0.5
% perch on a random tall tree (random site inside group's home range)
X(i,:)=(Rabbit_Location(1,:)-mean(X))-Cm(1,3)*((ub-lb)*Cm(1,4)+lb);
end
elseif abs(Escaping_Energy)<1
%% Exploitation:
% Attacking the rabbit using 4 strategies regarding the behavior of the rabbit
%% phase 1: surprise pounce (seven kills)
% surprise pounce (seven kills): multiple, short rapid dives by different hawks
r=rand(); % probablity of each event
if r>=0.5 && abs(Escaping_Energy)<0.5 % Hard besiege
X(i,:)=(Rabbit_Location)-Escaping_Energy*abs(Rabbit_Location-X(i,:));
end
if r>=0.5 && abs(Escaping_Energy)>=0.5 % Soft besiege
Jump_strength=2*(1-rand()); % random jump strength of the rabbit
X(i,:)=(Rabbit_Location-X(i,:))-Escaping_Energy*abs(Jump_strength*Rabbit_Location-X(i,:));
end
%% phase 2: performing team rapid dives (leapfrog movements)
if r<0.5 && abs(Escaping_Energy)>=0.5 % Soft besiege % rabbit try to escape by many zigzag deceptive motions
w1=2*exp(-(8*t/T)^2); % Non-linear control Parameter
Jump_strength=2*(1-rand());
X1=w1*Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-X(i,:));
if fobj(X1)>fobj(X(i,:)) % improved move?
X(i,:)=X1;
else % hawks perform levy-based short rapid dives around the rabbit
X2=w1*Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-X(i,:))+rand(1,dim).*Levy(dim);
if (fobj(X2)>fobj(X(i,:))) % improved move?
X(i,:)=X2;
end
end
end
if r<0.5 && abs(Escaping_Energy)<0.5 % Hard besiege % rabbit try to escape by many zigzag deceptive motions
% hawks try to decrease their average location with the rabbit
w1=2*exp(-(8*t/T)^2);
Jump_strength=2*(1-rand());
X1=w1*Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-mean(X));
if fobj(X1)>fobj(X(i,:)) % improved move?
X(i,:)=X1;
else % Perform levy-based short rapid dives around the rabbit
X2=w1*Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-mean(X))+rand(1,dim).*Levy(dim);
if (fobj(X2)>fobj(X(i,:))) % improved move?
X(i,:)=X2;
end
end
end
%%
end
end
t=t+1;
CNVG(t)=Rabbit_Energy;
end
end
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。





![[管理与领导-112]:IT人看清职场中的隐性规则 - 9 - 付出与回报的关系:先付出,后回报,不行就止损,这才是职场价值交换的本质](https://img-blog.csdnimg.cn/a5df59838d744fb0ad1b5752de323431.png)