**美丽的图论 **
Prüf 😉
对于 n 个顶点上的树的数量
n^(n-2),这是凯莱公式,用于计算 n 个顶点上的树的数量,被放置在一个由 4 个标记顶点组成的圆圈中。
使用 Figma 制作
在图论中,树只是一个没有环的图。

树在离散数学的许多现实世界应用中都很重要。从大脑中的神经元结构到机器学习中的决策树和计算机科学中的二叉搜索树。
更不用说你的亲人为之自豪的传统家谱了!
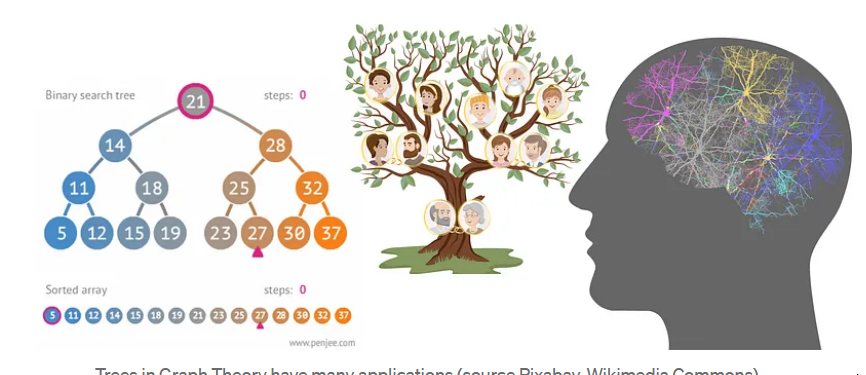
图论中的树有许多应用:Pixabay |Wikimedia Commons
n 个标记顶点上的树的数量由凯莱公式 n^(n − 2) 给出。
但是为什么会这样呢?
例如,这个公式告诉我们,使用从 1 到 4 标记的顶点,应该有 16 个树。
这实际上是正确的,这 16 个树在页眉图像中显示出来。但为什么树的数量应该是 4 × 4?
如果我们有从 1 到 5 标记的顶点,为什么应该有 5 × 5 × 5 = 125 个树?
如果我们有从 1 到 6 标记的顶点,为什么应该有 6 × 6 × 6 × 6 = 1296 个树?
让我们以 6 个顶点的示例进行调查!🧐
6 × 6 × 6 × 6 是从哪里来的?这意味着我们有 6 个连续选择的选项。这些连续的 4 个选择是什么?为什么有 6 个?
这就是 Prüfer 序列发挥作用的地方。现在你终于可以欣赏标题中的双关语了 🙄🤣
Prüfer 序列是一种巧妙的方法,可以将具有 n 个顶点的任何树编码成长度为 (n − 2) 的序列,其中每个数字可以取 1 到 n 中的任何值。
下面显示了一些 Prüfer 序列及其对应的树的示例。
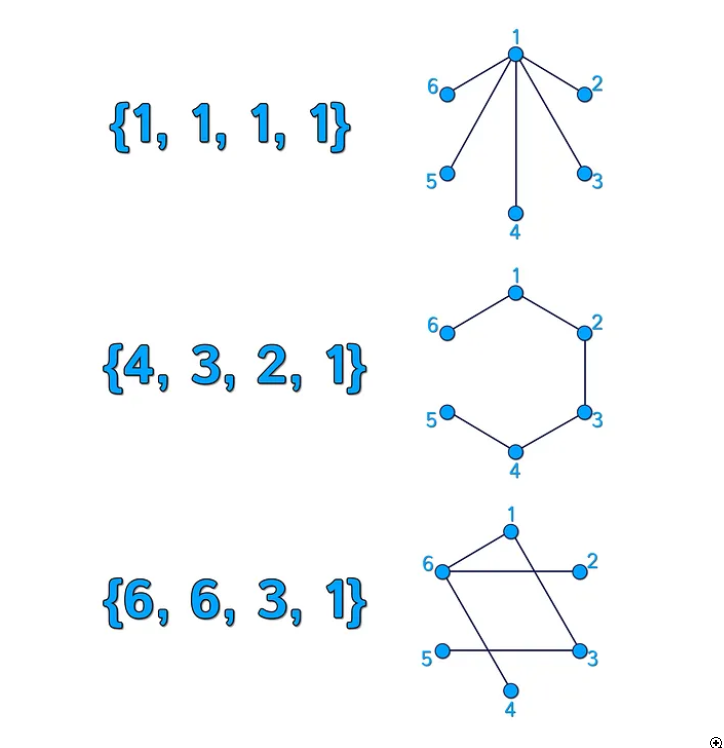
因为每个数字可以取 1 到 n 中的任何值,长度为 (n − 2) 的 Prüfer 序列的数量显然是 n^(n − 2)。
现在让我们解释为什么每个树都有唯一的 Prüfer 序列,反之亦然。
我们将使用上面显示的第三个示例,Prüfer 序列 {6, 6, 3, 1}。为给定的树创建 Prüfer 序列非常容易。
只需按升序连续删除树的叶子节点。树的叶子是度为 1 的顶点。
稍微正式一点:

因为我们会一直删除顶点,直到 T 的度为 2,所以这个算法必须经过 (n − 2) 次迭代,并输出一个包含 (n − 2) 个数字的列表。
下面的图表显示了从相应树中获取 Prüfer 序列 {6, 6, 3, 1} 需要的 4 个迭代。
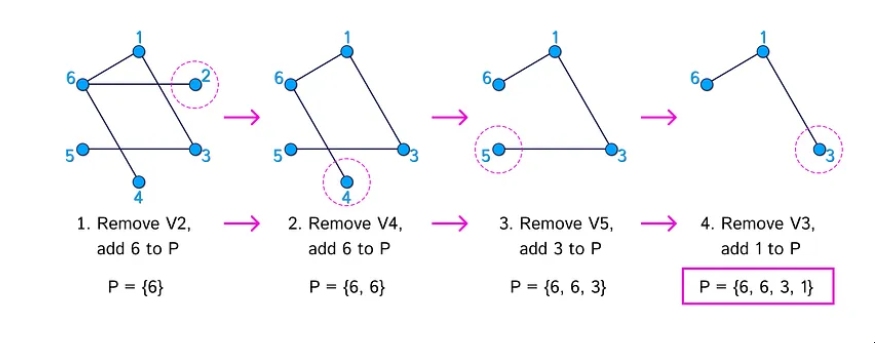
从相应树中获取 Prüfer 序列 {6, 6, 3, 1} 需要 4 个迭代。 现在来验证每个树获得的 Prüfer 序列都是唯一的。
如果我们仔细观察这个算法,实际上我们会发现每个步骤都只有一种选择。
在每个步骤中,具有最小标签的度为 1 的顶点是唯一的。而这个顶点的邻居是唯一的,因为这个顶点的度为 1
这种唯一性意味着将树映射到 Prüfer 序列的函数是单射的(没有两个树输出相同的 Prüfer 序列)。
但为了证明 Prüfer 序列的数量等于标记树的数量,我们需要进一步证明该函数是双射的。
也就是说,我们需要证明每个 Prüfer 序列也可以映射到唯一的树。
从序列构建树的算法本质上与我们之前所做的相反,但似乎更复杂,因为我们需要输出一棵树,而不仅仅是一个数字列表。
以下是显示与 Prüfer 序列 {6,6,3,1} 相关联的唯一树所需的五个步骤的图表。
为了好玩,再来一个例子。下面的图表显示了与 Prüfer 序列 {4,3,2,1} 相关联的唯一树所需的五个步骤。

再次,通过观察算法,我们可以看到每个步骤实际上只有一种选择。在每个步骤中,必须有一个唯一的 x,它是 L 中最小的标签,必须有一个唯一的 y,它是 P 中的第一个标签。

这证明了每个 Prüfer 序列也可以映射到唯一的树,因此标记树与 Prüfer 序列之间的映射是双射的。因此,Prüfer 序列的数量等于标记树的数量,即 n^(n − 2)。

现在,Mr. Prüfer (Heinz) 是如何在 1918 年提出这个美丽而巧妙的算法的直觉呢?
Prüfer 序列在图论中具有广泛的应用场景,特别是与标记树相关。以下是一些 Prüfer 序列的应用场景:
-
计算树的数量: Prüfer 序列可以用来计算给定顶点数的所有可能的标记树的数量。通过使用凯莱公式(Cayley's formula) n^(n − 2),其中 n 是顶点数,可以确定树的数量。这在组合数学和图论中非常有用。
-
网络拓扑分析: 在计算机网络和通信领域,Prüfer 序列可以用于分析网络拓扑结构和寻找最小生成树。它有助于理解网络中的连接方式和通信路径。
-
生物学和神经科学: Prüfer 序列被用来分析生物学中的分子结构和神经系统的连接。在生物信息学中,它可以用于描述蛋白质或基因之间的相互作用。
-
编码理论: Prüfer 序列的概念与编码理论相关,可以用于设计和分析错误检测和纠正编码。
-
排列和组合: Prüfer 序列可用于生成排列和组合的问题,特别是在解决与图论相关的组合问题时。
-
数据压缩: 在一些数据压缩算法中,Prüfer 序列可以用来表示树结构,从而减少数据存储需求。
总的来说,Prüfer 序列是一个强大的工具,可用于解决多种与图论、组合数学和网络结构相关的问题。它提供了一种紧凑而有效的方式来表示和分析树形结构,因此在多个领域都有实际应用。
当进行网络拓扑分析时,通常需要使用特定的网络拓扑数据来执行各种操作,例如查找最小生成树、计算网络中的节点关系、查找环路等。下面是一个Python示例,演示如何使用NetworkX库来创建一个简单的网络拓扑图并执行一些基本的分析操作。
首先,确保您已经安装了NetworkX库。您可以使用以下命令来安装它:
pip install networkx
接下来,以下是一个Python示例代码,用于创建一个简单的网络拓扑图,并查找最小生成树以及查找节点之间的最短路径:
import networkx as nx
import matplotlib.pyplot as plt
# 创建一个空的无向图
G = nx.Graph()
# 添加节点
G.add_node("A")
G.add_node("B")
G.add_node("C")
G.add_node("D")
G.add_node("E")
# 添加边(连接节点)
G.add_edge("A", "B", weight=2)
G.add_edge("A", "C", weight=1)
G.add_edge("B", "C", weight=3)
G.add_edge("B", "D", weight=5)
G.add_edge("C", "E", weight=4)
G.add_edge("D", "E", weight=7)
# 绘制图形
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, node_size=700, node_color='skyblue', font_size=10, font_color='black')
labels = nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos, edge_labels=labels)
# 查找最小生成树
minimum_spanning_tree = nx.minimum_spanning_tree(G)
print("Minimum Spanning Tree Edges:")
for edge in minimum_spanning_tree.edges(data=True):
print(edge)
# 查找节点之间的最短路径
shortest_path = nx.shortest_path(G, source="A", target="D", weight="weight")
print("Shortest Path from A to D:", shortest_path)
# 计算最短路径长度
shortest_path_length = nx.shortest_path_length(G, source="A", target="D", weight="weight")
print("Shortest Path Length from A to D:", shortest_path_length)
# 显示图形
plt.show()
这个示例首先创建了一个简单的无向图,然后添加了节点和边。接下来,它使用NetworkX库来查找最小生成树和节点之间的最短路径。
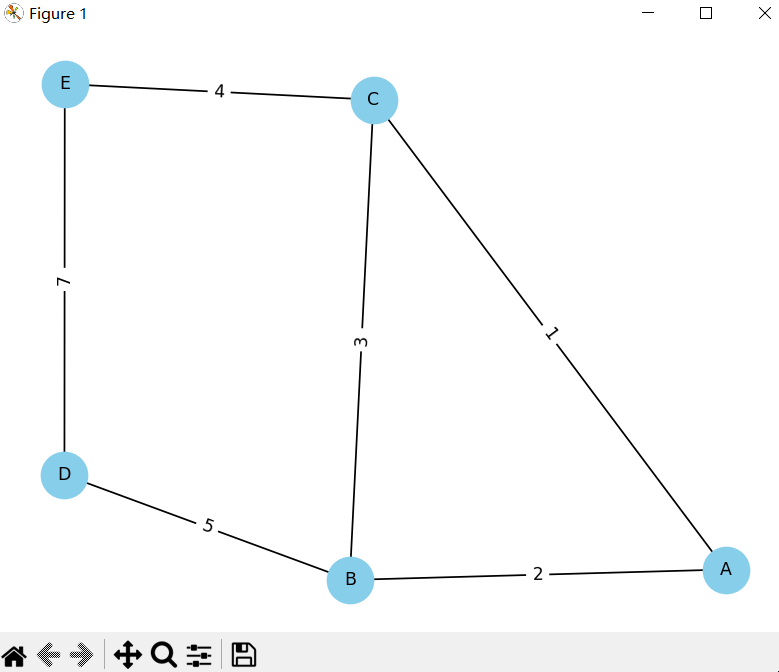
A 到 D 之间的最小生成树:D: ['A', 'B', 'D']
A 到 D 之间的最短路径是:7
详见输出👇
Minimum Spanning Tree Edges:
('A', 'C', {'weight': 1})
('A', 'B', {'weight': 2})
('B', 'D', {'weight': 5})
('C', 'E', {'weight': 4})
Shortest Path from A to D: ['A', 'B', 'D']
Shortest Path Length from A to D: 7
最后,通过matplotlib库绘制了网络拓扑图,并在图上标记了权重信息。
请注意,这只是一个简单的示例,用于演示如何使用NetworkX进行网络拓扑分析。
在实际应用中,您可能会处理更复杂的网络结构和更多的数据。根据您的具体需求,您可以进一步扩展和自定义此示例。
这对我来说是一个谜!如果您对其背后的直觉有想法,请随时留下评论。 😊