文章目录
- 灵敏度分析详细步骤
- 单参数分析
灵敏度分析详细步骤
灵敏度分析是一种用于确定输入参数变化对模型输出结果的影响程度的方法。以下是进行灵敏度分析的一般步骤:
- 确定模型:选择需要进行灵敏度分析的模型,该模型必须具有可变参数和可计算的输出结果。
- 选择参数:确定需要进行灵敏度分析的参数,并确定它们的范围和变化方式。
- 运行模型:使用所选的参数运行模型,并记录输出结果。
- 分析数据:使用统计方法,例如相关性分析或回归分析,对数据进行分析。
- 做出结论:根据数据分析的结果,确定每个参数对模型输出结果的影响程度,并根据这些结论来优化模型参数。
灵敏度分析可以使用各种工具和技术来实现,例如:
- 单参数分析:一个参数一个参数地变化,看模型输出结果如何变化。
- Morris方法:用少量的样本点,在参数空间中随机地选取点,并改变一个参数,计模型的输出。通过这些输出结果来计算各个参数的灵敏度指数。
- Sobol方法:使用Latin Hypercube Sampling (LHS)和Monte Carlo方法,在参数空间中随机地选取点。Sobol方法计算每个参数的一次和二次效应,以确定各个参数对输出结果的贡献。
灵敏度分析是一种有用的方法,可以帮助我们了解模型输出结果受输入参数的影响,进而优化模型的参数,提高模型的准确性和预测能力。
单参数分析
修改模型参数,可视化模型性能。以随机森林的树数量为例进行分析:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
# 加载数据集
data = load_boston()
# 定义输入和输出变量
X = data['data']
y = data['target']
# 定义不同参数大小的范围
param_range = [10, 50, 100, 200, 300]
# 定义空列表用于存储模型性能
train_scores_mean = []
train_scores_std = []
test_scores_mean = []
test_scores_std = []
# 循环遍历不同的参数大小
for param in param_range:
# 创建一个随机森林回归模型
model = RandomForestRegressor(n_estimators=param)
# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
# 训练模型
model.fit(X_train, y_train)
# 预测测试数据集和训练数据集
y_pred_train = model.predict(X_train)
mse_train = mean_squared_error(y_train, y_pred_train)
train_scores_mean.append(np.mean(mse_train))
train_scores_std.append(np.std(mse_train))
y_pred_test = model.predict(X_test)
mse_test = mean_squared_error(y_test, y_pred_test)
test_scores_mean.append(np.mean(mse_test))
test_scores_std.append(np.std(mse_test))
# 可视化结果
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(param_range, train_scores_mean, label='Train MSE')
ax.fill_between(param_range, np.array(train_scores_mean) - np.array(train_scores_std),
np.array(train_scores_mean) + np.array(train_scores_std), alpha=0.1)
ax.plot(param_range, test_scores_mean, label='Test MSE')
ax.fill_between(param_range, np.array(test_scores_mean) - np.array(test_scores_std),
np.array(test_scores_mean) + np.array(test_scores_std), alpha=0.1)
ax.set_xlabel('Number of estimators', fontsize=14)
ax.set_ylabel('Mean Squared Error', fontsize=14)
ax.tick_params(axis='both', which='major', labelsize=12)
ax.legend(fontsize=12)
ax.grid(axis='y')
plt.tight_layout()
plt.show()
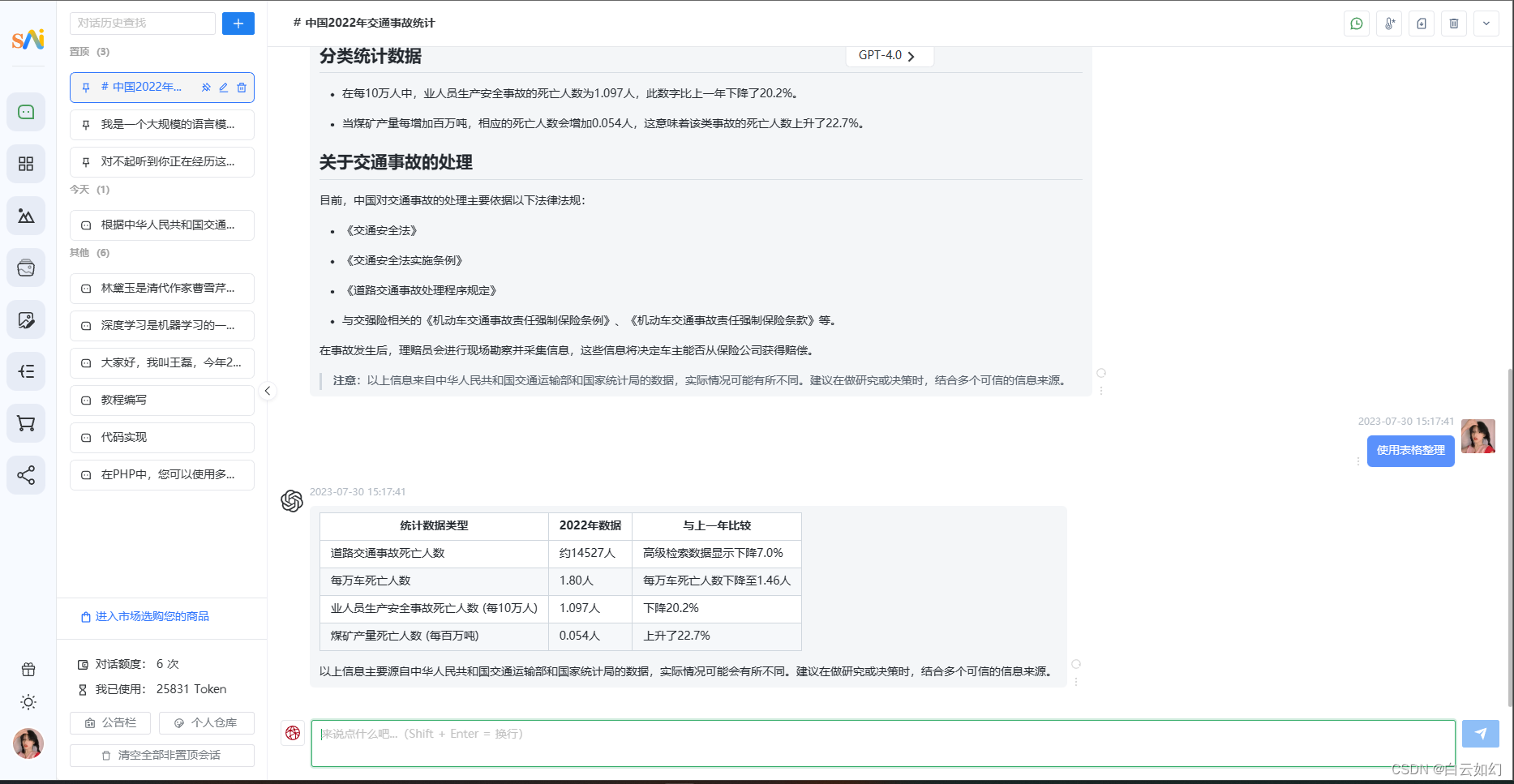
如下:
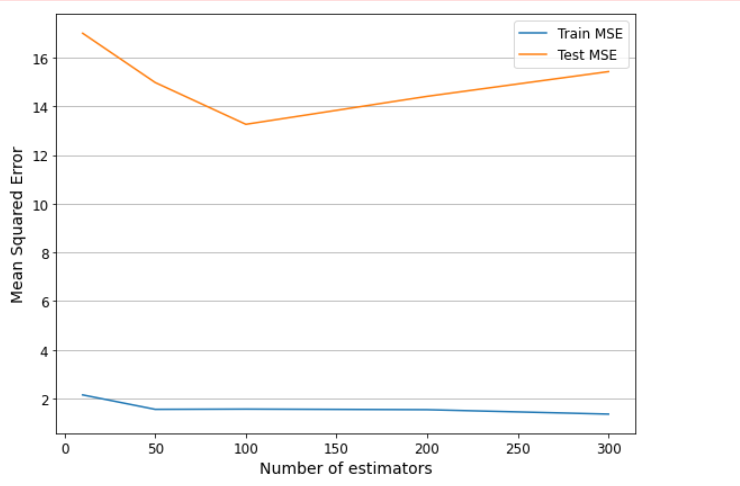
其中 x 轴表示 n_estimators 参数的大小,y 轴表示均方误差。图形中的两条曲线分别表示训练集和测试集上的均方误差随参数大小的变化情况。阴影区域表示每个参数大小对应的训练集和测试集均方误差的标准差范围。通过观察图形,我们可以确定最优的参数大小,以获得最佳的模型性能。例如,在这个示例中,当 n_estimators=100 时,测试集上的均方误差最低,因此这个参数大小可能是最优的选择。我们还可以观察到,随着 n_estimators 参数的增加,测试集上的均方误差呈现先降低后增加的趋势,这是因为过多的树可能会导致过拟合。