关于LORA部分的讲解，我们将分为**“原理篇”和“源码篇”**。

在原理篇中，我们将通过图解的方式，详细分析LoRA怎么用、为什么能奏效、存在哪些优劣势等核心问题。特别是当你在学习LoRA时，如果对“秩”的定义和作用方式感到迷惑，那么本文也许能提供一些具象化的解读方式。

技术交流

技术要学会分享、交流，不建议闭门造车。一个人可以走的很快、一堆人可以走的更远。

相关资料、数据、技术交流提升，均可加我们的交流群获取，群友已超过2000人，添加时最好的备注方式为：来源+兴趣方向，方便找到志同道合的朋友。

方式①、添加微信号：mlc2060，备注：来自CSDN + 技术交流
方式②、微信搜索公众号：机器学习社区，后台回复：加群

在源码篇中，我们将一起剖析微软LoRA源码，并帮助大家在google colab平台上使用免费GPU，搭建LoRA微调环境，使得每个人可以亲自动手跑一遍原生LoRA代码，加深对LoRA运作机制的理解（不要钱的快乐才是真快乐）。

一、全参数微调

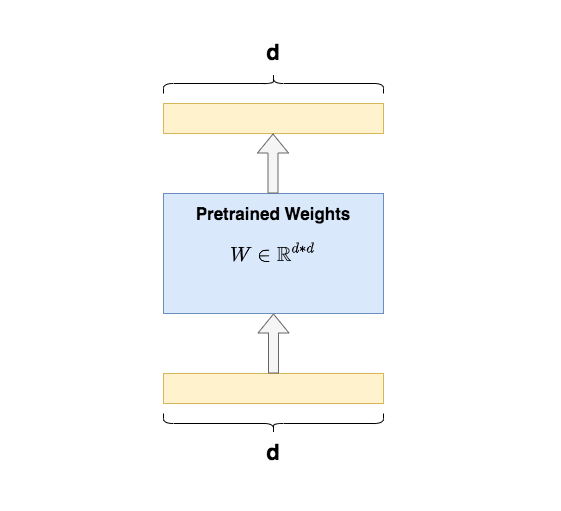
我们知道，微调的含义，就是把已经训练好的模型（pretrained model）拿来，给它吃特定的下游任务数据，使得模型在预训练权重上继续训练，直至满足下游任务性能标准。预训练模型就像一个特征提取器，能够基于先前训练数据中学到的经验，为我们提取有效的特征，大大提升下游任务的训练效果和收敛速度。

全量微调指的是，在下游任务的训练中，对预训练模型的每一个参数都做更新。例如图中，给出了Transformer的Q/K/V矩阵的全量微调示例，对每个矩阵来说，在微调时，其d*d个参数，都必须参与更新。

全量微调的显著缺点是，训练代价昂贵。例如GPT3的参数量有175B，我等单卡贵族只能望而却步，更不要提在微调中发现有bug时的覆水难收。同时，由于模型在预训练阶段已经吃了足够多的数据，收获了足够的经验，因此我只要想办法给模型增加一个额外知识模块，让这个小模块去适配我的下游任务，模型主体保持不变（freeze）即可。

那这样的知识小模块，具体要怎么添加呢？

二、Adapter Tuning与Prefix Tuning

我们来看在LoRA出现前，两种主流的局部微调办法：Adapter Tuning与Prefix Tuning。这也是LoRA的原始论文中，重点比对的两种微调方式。

2.1 Adapter Tuning

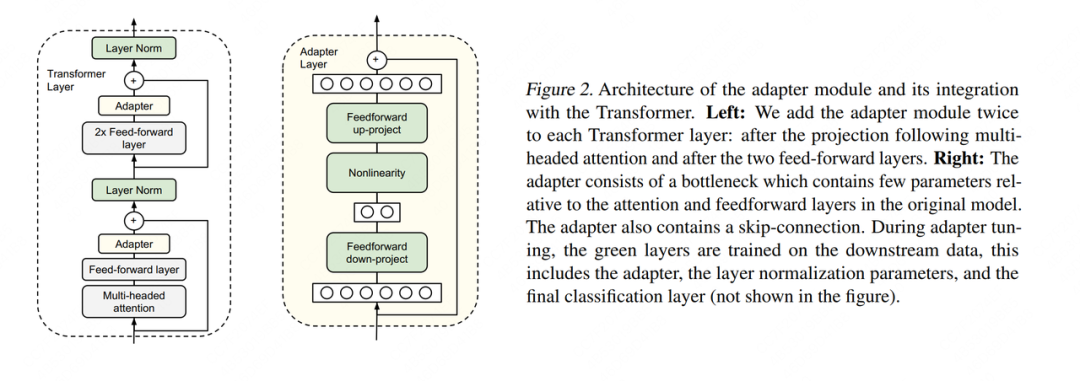
Adapter Tuning的方法有很多种，这里我们举出Houlsby et al. ,2019提出的方法，这也是LoRA论文中提及这项技术时所引用的第一篇文章。

图例中的左边是一层Transformer Layer结构，其中的Adapter就是我们说的“额外知识模块”；右边是Adatper的具体结构。在微调时，除了Adapter的部分，其余的参数都是被冻住的（freeze），这样我们就能有效降低训练的代价。Adapter的内部架构不是本文所述的重点，这里我们就不再介绍了。

但这样的设计架构存在一个显著劣势：添加了Adapter后，模型整体的层数变深，会增加训练速度和推理速度，原因是：

• 需要耗费额外的运算量在Adapter上

• 当我们采用并行训练时（例如Transformer架构常用的张量模型并行），Adapter层会产生额外的通讯量，增加通讯时间

2.2 Prefix Tuning

Prefix Tuning的方法也有很多种，这里我们选取Li&Liang,2021这一篇进行简述。在这篇中，作者通过对输入数据增加前缀（prefix）来做微调。当然，prefix也可以不止加载输入层，还可以加在Transformer Layer输出的中间层，感兴趣的朋友可以查找论文自行研究。

如图所示，对于GPT这样的生成式模型，在输入序列的最前面加入prefix token，图例中加入2个prefix token，在实际应用中，prefix token的个数是个超参，可以根据模型实际微调效果进行调整。对于BART这样的Encoder-Decoder架构模型，则在x和y的前面同时添加prefix token。在后续微调中，我们只需要冻住模型其余部分，单独训练prefix token相关的参数即可，每个下游任务都可以单独训练一套prefix token。

那么prefix的含义是什么呢？prefix的作用是引导模型提取x相关的信息，进而更好地生成y。例如，我们要做一个summarization的任务，那么经过微调后，prefix就能领悟到当前要做的是个“总结形式”的任务，然后引导模型去x中提炼关键信息；如果我们要做一个情感分类的任务，prefix就能引导模型去提炼出x中和情感相关的语义信息，以此类推。这样的解释可能不那么严谨，但大家可以大致体会一下prefix的作用。

Prefix Tuning虽然看起来方便，但也存在以下两个显著劣势：

• 较难训练，且模型的效果并不严格随prefix参数量的增加而上升，这点在原始论文中也有指出

• 会使得输入层有效信息长度减少。为了节省计算量和显存，我们一般会固定输入数据长度。增加了prefix之后，留给原始文字数据的空间就少了，因此可能会降低原始文字中prompt的表达能力。

三、什么是LoRA

总结一下，全参数微调太贵，Adapter Tuning存在训练和推理延迟，Prefix Tuning难训且会减少原始训练数据中的有效文字长度，那是否有一种微调办法，能改善这些不足呢？

在这样动机的驱动下，作者提出了LoRA (Low-Rank Adaptation，低秩适配器) 这样一种微调方法。我们先抛开对“低秩”、“适配器”这样抽象词语的解释，我们先来看LoRA长什么样，要怎么用。在下一节中，我们再来详细解释“低秩”作用的原理。

3.1 LoRA整体架构

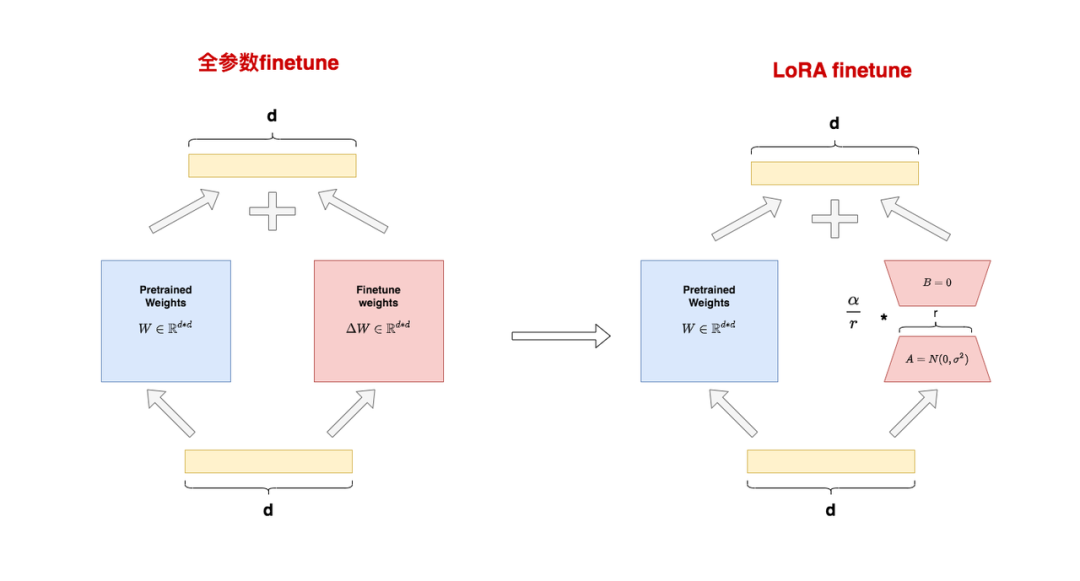
图中左侧表示“全参数finetune”的场景。我们将参数分成了两个部分：

• ：预训练权重

• ：finetune增量权重

之所以这么拆分，是因为全参数finetune可以理解成“冻住的预训练权重” + “微调过程中产生的权重更新量”。 设输入为，输出为，则有：

图中右侧表示“LoRA finetune”的场景。在LoRA中，我们用矩阵A和B来近似表达：

• ：低秩矩阵，其中被称为“秩”，对采用高斯初始化。

• ：低秩矩阵，对B采用零初始化。

经过这样一番拆分，我们将改写成的形式，使得微调参数量从d*d降低至2*r*d，同时不改变输出数据的维度，即在LoRA下我们有:

另外，在原论文中提到过对于两个低秩矩阵，会用超参****（一个常数）来做调整，但没有说明这个超参的作用位置。在读完LoRA的源码后，我发现这个超参是作为scaling rate直接和低秩矩阵相乘的，也就是最终的输出为：

在实操中，一般取，例如在LoRA源码对GPT2微调，做NLG任务时，就取。我们会在后文详细介绍这个scaling rate的作用，以及“秩”的具体含义。

A和B的初始化方法

需要注意的是，这里对采用高斯初始化，对采用零初始化的目的是，让训练刚开始时的值为0，这样不会给模型带来额外的噪声。那么你可能想问，那我对做零初始化，对做高斯初始化行不行呢？反正看起来只要让****初始化为0就行？

针对这个问题，我在github issue上找到了LoRA一作的回答：

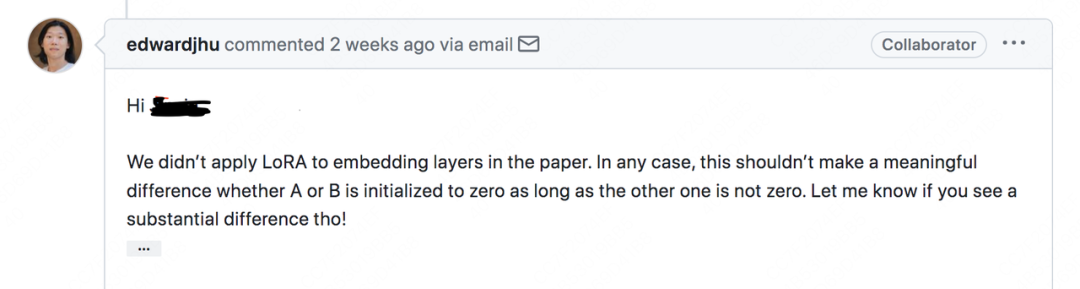
简单来说，当前作者还没有发现转换初始化方式产生的显著区别，只要这两者中任意一者为0，另一者不为0即可。

3.2 LoRA的训练和推理过程

在3.1中，我们介绍了LoRA的整体架构：在原始预训练矩阵的旁路上，用低秩矩阵A和B来近似替代增量更新。你可以在你想要的模型层上做这样的操作，比如Transformer中的、MLP层的权重、甚至是Embedding部分的权重。在LoRA原始论文中，只对Attention部分的参数做了低秩适配，但在实际操作中，我们可以灵活根据需要设置实验方案，找到最佳的适配方案（有钱万事通）。

3.2.1 训练

在训练过程中，我们固定住预训练权重，只对低秩矩阵和进行训练。在保存权重时，我们只需保存低秩矩阵的部分即可。按照LoRA论文中的统计，这样的操作使得在微调GPT3 175B时，显存消耗从1.2TB降至350GB；当r=4时，最终保存的模型从350GB降至35MB，极大降低了训练的开销。

关于训练部分，我们再来看一个有趣的问题：总体上来看，LoRA对显存的节约是显著的，但是在训练的每一时刻，LoRA都能做到节省显存吗？

考虑backward时对计算梯度，根据（为了敲公式方便，暂时忽略掉一项），我们有：

注意这一项，你会发现，它和预训练权重的维度d*d 一模一样，也就是为了计算的梯度，我们需要用到和全参数微调过程中一样大小的中间值结果。因此对LoRA来说，这一层的峰值显存，和全量微调基本是一致的（算上一项的话则高于全量微调）。

但是为什么LoRA又能从整体上降低显存使用呢，因为：

• LoRA并不是作用在模型的每一层，例如论文里的LoRA只作用在attention部分

• LoRA虽然会导致某一层的峰值显存高于全量微调，但计算完梯度后，这个中间结果就可以被清掉了，不会一致保存

• 当待训练权重从d*d降为2*r*d时，需要保存的optimizer states也减少了（那可是fp32）。

3.2.2 推理

在推理过程中，我们按照的方式，合并低秩矩阵和预训练权重，然后正常做forward推理。这样我们完全不会更改模型的架构，因此不会像Adapter Tuning一样产生推理上的延时。下图展示了论文中的实验效果，推理时长的单位是milliseconds，可以发现，LoRA的推理速度显著高于Adapter Tuning。

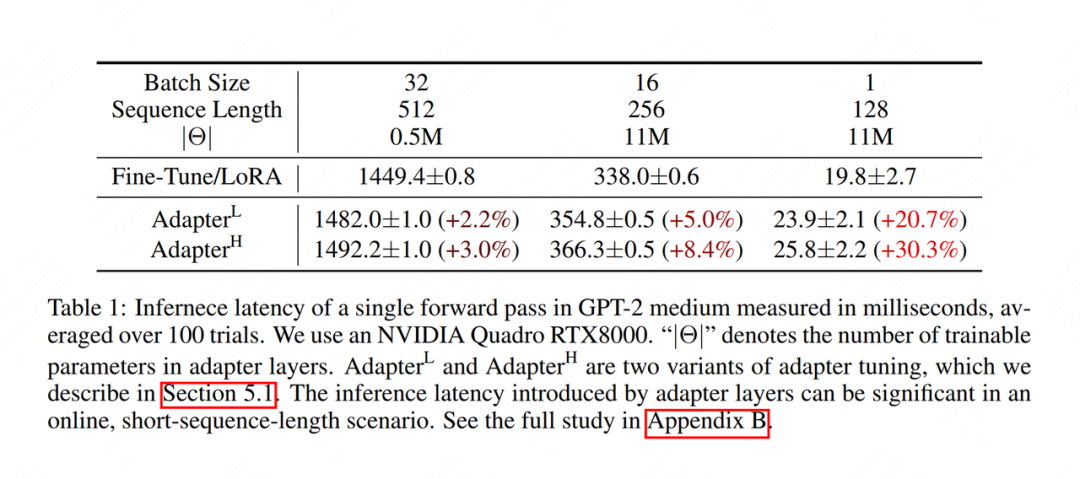
在切换不同下游任务时，我们可以灵活从中移除低秩权重的部分。例如我们先做下游任务A，做完后通过合并权重，并单独保留低秩权重。当我们切换到下游任务B时，我们可以通过从中减去低秩权重部分，然后再开启新的LoRA微调。也就是说，每个下游任务，都可以有自己的一套低秩权重。

**你可能想问，在每次微调结束后，我一定要把低秩权重合进****中吗？我可以将“预训练权重”和“低秩权重”分开存储吗？**当然没问题啦，LoRA是很灵活的，你完全可以根据自身需要，改写代码，决定权重的保存方式，只要掌握一个核心原则：不管是合还是不合，你总有办法能区分出预训练和LoRA的部分，就行。在源码解读篇中，我们会再详细来看这点。

恭喜你！到这一步你已经掌握了LoRA的架构，是不是很简单，是不是跃跃欲试？但是，作为一名合格的炼丹师，为了能对训练过程更好debug，我们还要需要更深入研究LoRA的原理。

四、LoRA低秩适配的原理

在前文中，我们曾反复提到“秩”的概念，并说明LoRA的秩即为超参，同时，我们也不断强调是的近似。在这一节中，我们将具象化地来看看“秩”，并说明为何是“近似”，在了解这些后，我们就能来解读超参****的作用，并掌握一定的炼丹感觉了。

4.1 什么是秩

我们首先来看一个矩阵A：

A = [[1, 2, 3],
     [2, 4, 6],
     [3, 6, 9]]

该矩阵中，row2 = row1 * 2，row3 = row1*3，也就是说，矩阵中的每一行，都可以通过第一行线性表示。

我们再来看一个矩阵B：

B = [[1, 2, 3],
     [7, 11, 5],
     [8, 13, 8]]

该矩阵中，任意一行，总可以用其他两行的线性组合来表示。

我们最后再来看一个矩阵C：

C = [[1, 0, 0],
     [0, 1, 0],
     [0, 0, 1]]

该矩阵中，任意一行，都不能从其余行的线性组合中推导而来。

调用np.linalg.matrix_rank函数，我们可以算出任意矩阵的秩，上面三个矩阵的秩分别为：

A = np.array(A)
B = np.array(B)
C = np.array(C)

print("Rank of A:", np.linalg.matrix_rank(A)) # 1
print("Rank of B:", np.linalg.matrix_rank(B)) # 2
print("Rank of C:", np.linalg.matrix_rank(C)) # 3

对矩阵A来说，由于只要掌握其中的任意一行，其余行都可以由这一行线性推导而来，因此A的秩是1。

对矩阵B来说，由于只要掌握其中的任意两行，其余行都可以由这两行线性组合推导而来，因此B的秩是2。

对矩阵C来说，由于必须完全掌握三行，才能得到完整的C，因此C的秩是3。

看到这里，你是不是已经对秩有了感性的理解了？秩表示的是矩阵的信息量。如果矩阵中的某一维，总可以通过其余维度线性推导而来，那么对模型来说，这一维的信息是冗余的，是重复表达的。对A和B的情况，我们称为秩亏（rank deficient），对C的情况，我们称为满秩（full rank）。更严谨的数学定义，大家可以参考《线性代数》（狗头）。

有了对秩的这层认识，我们自然会想到，**全参数微调中的增量权重可能也存在冗余的信息，因此我们并不需要用完整的d*d尺寸来表示它。**那么，我们要如何找出中真正有用的特征维度呢？SVD分解（奇异值分解），可以帮我们解决这个问题

4.2 SVD分解

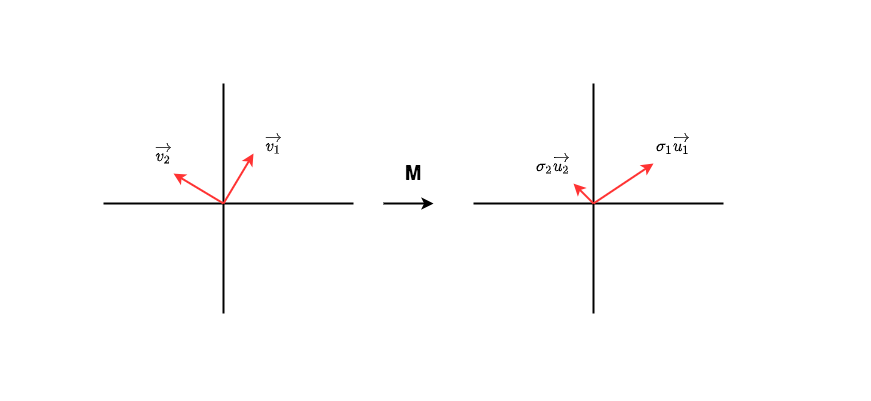
如图，矩阵是我们需要做信息量检查的矩阵。假设在输入数据的特征空间中，存在一组正交的单位向量，经过的变换后，它们变成另一组正交向量，其中也是一组正交的单位向量，分别表示对应方向上的模。上面这一顿变幻，可以写成：

稍加改写，就有：

不难发现，中隐含了对“信息量”的提示。在本例中经过的转换投射到上时，强调了在1方向上蕴含的信息。

现在再宽泛一些，如果我们能找到这样的一组和，并令矩阵的值从大到小进行排列，那么我们不就能对进行拆解，同时在拆解过程中，找出所强调的那些特征方向了吗？也就是说：

当我们找到这样的矩阵后，我们再从这三者中取出对应的top r 行（或列），不就相当于关注到了最强调的那几维特征，进而就能用更低维的矩阵，来近似表达****了？按这种思维拆解M的方法，我们称为SVD分解（奇异值分解）。在本篇里我们不讲述它的具体方法，感兴趣的朋友们，欸，又可以参考《线性代数》。

我们再通过一个代码例子，更直观地感受一下这种近似，大家注意看下注释（例子改编自：https://medium.com/@Shrishml/lora-low-rank-adaptation-from-the-first-principle-7e1adec71541）

import torch
import numpy as np
torch.manual_seed(0)

# ------------------------------------
# n：输入数据维度
# m：输出数据维度
# ------------------------------------
n = 10
m = 10

# ------------------------------------
# 随机初始化权重W
# 之所以这样初始化，是为了让W不要满秩，
# 这样才有低秩分解的意义
# ------------------------------------
nr = 10
mr = 2
W = torch.randn(nr,mr)@torch.randn(mr,nr)

# ------------------------------------
# 随机初始化输入数据x
# ------------------------------------
x = torch.randn(n)

# ------------------------------------
# 计算Wx
# ------------------------------------
y = W@x
print("原始权重W计算出的y值为:\n", y)

# ------------------------------------
# 计算W的秩
# ------------------------------------
r= np.linalg.matrix_rank(W)
print("W的秩为: ", r)

# ------------------------------------
# 对W做SVD分解
# ------------------------------------
U, S, V = torch.svd(W)

# ------------------------------------
# 根据SVD分解结果，
# 计算低秩矩阵A和B
# ------------------------------------
U_r = U[:, :r]
S_r = torch.diag(S[:r])
V_r = V[:,:r].t()

B = U_r@S_r # shape = (d, r)
A = V_r     # shape = (r, d)

# ------------------------------------
# 计算y_prime = BAx
# ------------------------------------
y_prime = B@A@x

print("SVD分解W后计算出的y值为:\n", y)

print("原始权重W的参数量为: ", W.shape[0]*W.shape[1])
print("低秩适配后权重B和A的参数量为: ", A.shape[0]*A.shape[1] + B.shape[0]*B.shape[1])

输出结果为：

原始权重W计算出的y值为:
 tensor([ 3.3896,  1.0296,  1.5606, -2.3891, -0.4213, -2.4668, -4.4379, -0.0375,
        -3.2790, -2.9361])
W的秩为:  2
SVD分解W后计算出的y值为:
 tensor([ 3.3896,  1.0296,  1.5606, -2.3891, -0.4213, -2.4668, -4.4379, -0.0375,
        -3.2790, -2.9361])
原始权重W的参数量为:  100
低秩适配后权重B和A的参数量为:  40

参数量变少了，但并不影响最终输出的结果。通过这个例子，大家是不是能更好体会到低秩矩阵的作用了呢～

4.3 LoRA低秩适配

好，那既然SVD分解这么有效，那我直接对做SVD，找到对应的低秩矩阵，不就大功告成了吗？

想法虽然好，但困难是明显的：能直接做SVD的前提是****是确定的，而现实中作为全参数微调中的权重增量，如果你不全参数微调一遍，又怎么能知道长什么样呢？而如果你做了全量微调，那还要低秩适配做什么呢？

欸，你可能又想：那我能不能对预训练权重做SVD呢，因为是确定的呀。

想法虽然好，但逻辑是不合理的：我们说过，微调的目的是给模型注入和下游任务相关的领域新知识。也就是说，和的表达含义是不同的，前者是新知识，后者是旧知识，我们的目的是要去新知识中拆解信息量丰富的维度。

好，那既然通过数学方法直接做SVD行不通，那就让模型自己去学怎么做SVD吧！因此LoRA最终的低秩适配策略是：我把秩当成一个超参，再让模型自己去学低秩矩阵，这不就简单又省事吗！

行，到这里我们已经具象化地了解了LoRA低秩适配的原理了，也知道和所表达含义的差异了，现在，我们可以来看前文遗留的问题：超参****是什么意思？

4.4 超参

我们先来看论文对的解释：

这段话大致意思是说，在我们采用Adam做优化器时，调整的作用就相当于调整learning rate。一般而言，我们把设置为我们第一次做实验时设置的，然后就把固定下来，之后只调整即可，这样做的好处是当我们尝试不同的时，我们不需要再去调整别的超参了。

不知道大家第一次读到这段话是什么感受，反正我是没有读懂。google搜了一遍，也没找到具体的解释。直到我按顺序捋了一遍LoRA低秩适配的设计思想后，我好像领悟了一些，下面我来谈谈我的个人见解。

首先，回顾一下我们的输出计算方法为：

其中，表示预训练权重（旧知识），表示增量权重的近似（新知识）。理论上说，当较小时，我们提取的是中信息含量最丰富的维度，此时信息精炼，但不全面；当较大时，我们的低秩近似越逼近，此时信息更加全面，但带来的噪声也越多（含有很多冗余无效的信息）。

基于这个猜想，当我们第一次做实验时，我们会尽量把调得大些，例如32、64，并假设在这个秩下，低秩权重已经非常近似了，因此这时我们设置，意味着我们假定LoRA低秩微调的效果和全参数微调持平。

那么接下来，我们肯定就要往小的进行尝试了。这时我们把固定住，意味着随着的减小，会越来越大，我们这样做的原因是：

• 当越小时，低秩矩阵表示的信息精炼，但不全面。我们通过调大，来放大forward过程中新知识对模型的影响。

• 当越小时，低秩矩阵表示的信息精炼，噪声/冗余信息少，此时梯度下降的方向也更加确信，所以我们可以通过调大，适当增加梯度下降的步伐，也就相当于调整learning rate了。

好，到这里，我们已经一起学完了LoRA低秩适配的核心思想了。我们前面说过，因为无法用SVD做直接分解，所以作者寄希望于LoRA能**“学习”**到真正的低秩分解矩阵，但是怎么证明LoRA学到的东西就和SVD分解出来的东西有关系呢？接下来，我们一起来解读作者的实验。

五、LoRA实验：验证低秩矩阵的有效性

5.1 整体效果

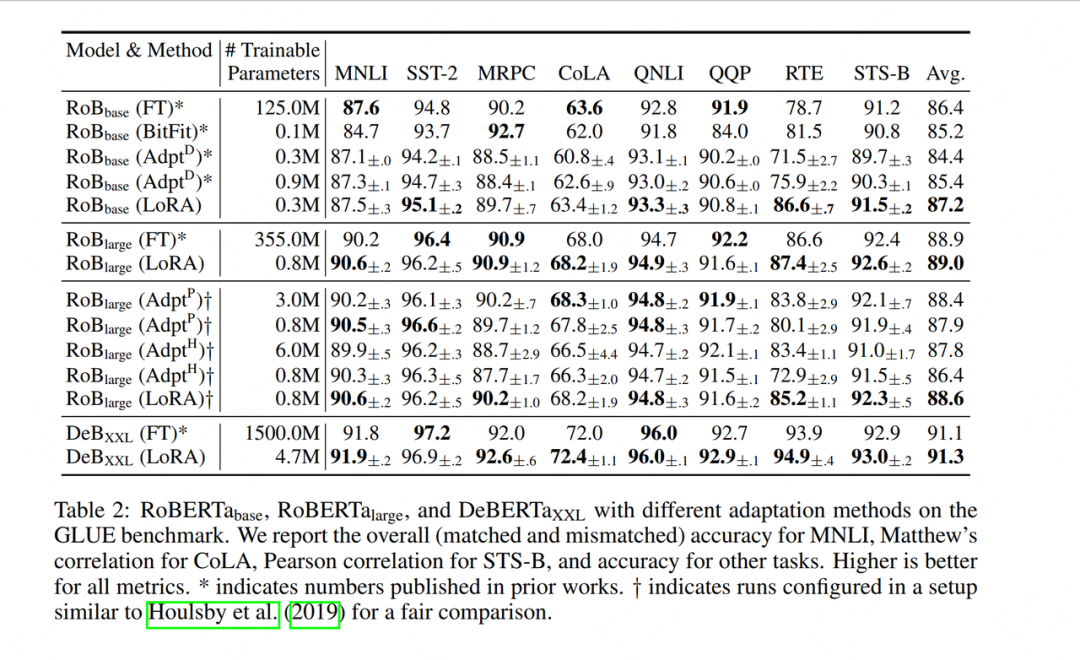
首先，作者将LoRA和其余微调方法（全参数微调，Adatper Tuning等）做了比较。纵列表示不同的微调模型，横列表示不同的数据集，加粗部分表示最好的效果指标。可以发现，无论是在各个数据集微调准确率指标上，还是在最后平均微调准确率指标上（Avg.），LoRA都取得了不错的表现，而且它可训练的参数量也非常小。

5.2 低秩矩阵信息量验证

我们前面说过，当越小时，低秩矩阵所含的信息越精炼，但同时也可能越不全面。那么到底要取多少才合适呢？

5.2.1 直接验证不同r值下的微调效果

尽管理论上我们可以在模型的任意一层嵌入低秩适配器（比如Embedding， Attention，MLP等），但LoRA中只选咋在Attention层嵌入，并做了相关实验（论文中也鼓励读者可以多做别的尝试），我们来看下Attention层的实验效果：

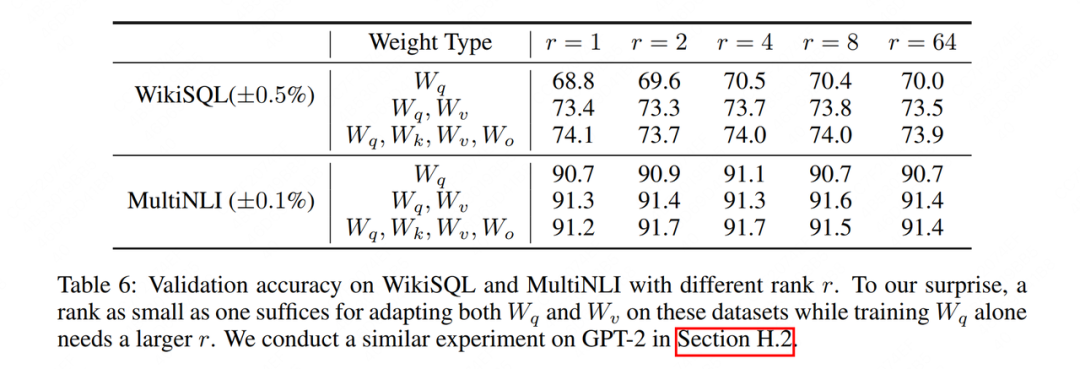
WikiSQL和MultiNLI是用于微调的数据集，Weight Type指明在Attention的哪一部分做了低秩适配。可以发现，于的效果几乎持平，甚至还略优于。这更加说明了“低秩”的有效性。为了更具象化地验证这一点，我们进一步来看和这两个低秩空间的相交程度。

5.2.2 不同低秩空间的相交程度

假设和分别是在和下训练出来的低秩矩阵，我们现在想做这么一件事：

• 从中取出个信息最丰富的维度（其中）

• 从中取出个信息最丰富的维度（其中）

• 计算这个维度和个维度的相交程度，以此来确定两个低秩矩阵间信息的重合度

欸那我怎么找出top个信息最丰富的维度呢？别忘了，我们有SVD方法，且这回和都是确定的了。所以，我们可以对低秩矩阵，再做SVD分解，然后分别得到这两者的右奇异矩阵（也就是前文说的），但LoRA论文里，用来表示右奇异矩阵，那么我们也入乡随俗把，令：

• 表示的右奇异矩阵，表示该右奇异矩阵信息量最丰富的个维度（复习一下前文，根据判断信息含量）

• 表示的右奇异矩阵，表示该右奇异矩阵信息量最丰富的个维度。

好，明确了这些定义后，我们可以来看的个特征维度，与的个特征维度的相交程度计算了，这个相交指标也被称为"Grassmann distance"。

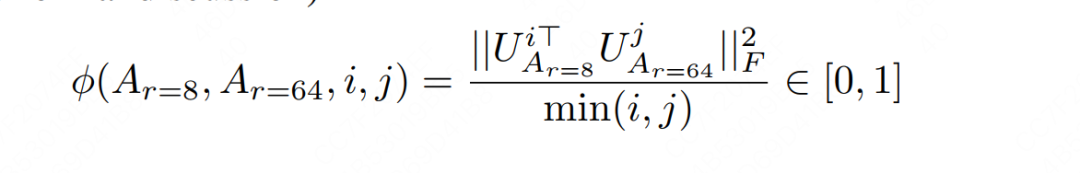
从上式可知，相交程度（Grassmann distance）位于之间，该值越大，表示相应的两个子空间越相似。感兴趣的朋友，可以参考论文附录G部分的相关证明。我们这里只关注结论。

好，把这个指标计算完了，那就可视化一波呗，所以作者继续给出了如下四张图：

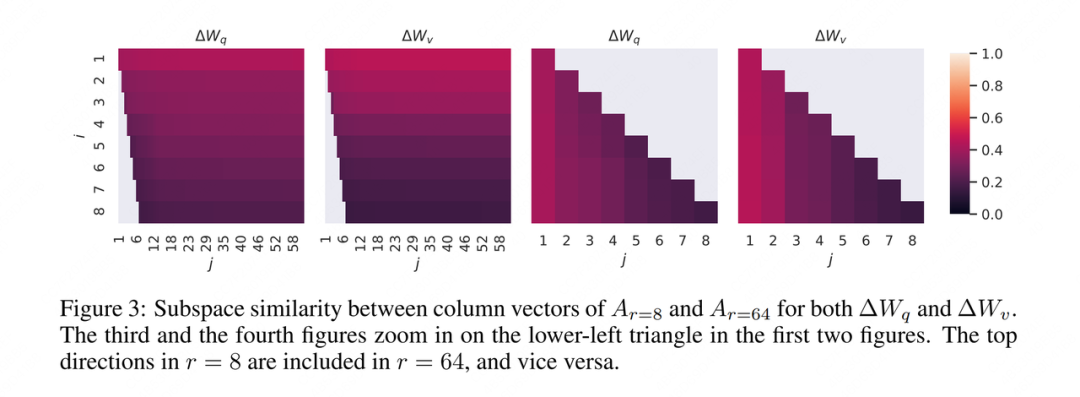
不知道你们第一次看到这张图是什么感觉，反正我是没看懂（欸这话怎么感觉在哪听过一次）。所以以下又是我（不负责任）的解读。

首先，作者是在上都做了低秩分解，所以1、3图和2、4图分别为一组，我们就选1、3图来看吧。

其次，作者做这个实验的目的，其实是想看高秩空间中到底包含了多少低秩空间的信息，这样才能解释为什么和的效果基本持平。

所以作者在计算Grassmann distance和绘制图表时的逻辑是：

• 对，当时，我想和的进行相似度计算，这样我就能知道，中最丰富的那1维信息，究竟包含了多少在的中。

• 对，当时，我想和的进行相似度计算，这样我就能知道，中最丰富的那2维信息，究竟包含了多少在的中。

• 以此类推，因为我想验证的是大秩空间()对小秩空间()的包含程度，所以时，我只绘制的部分，其余部分不绘制。所以才有了图1中，左下角的那一片空白。

• 那的部分，也就是小秩空间对大秩空间中top维度的包含程度，虽然我没绘制在图1里，但我可以单独拿出来绘制在图3中。所以图3其实是图1左下角缺失部分的填充。

好，解释完这一点，我们再具体来看图例。颜色越浅，表示相似度越高。在图1中，我们不难发现这一行的颜色是最浅的，随着的增加，颜色逐渐变深。这说明小秩空间中，信息量越高的那几维特征，和大秩空间的相交度越高，因此它们也是小秩空间表现能持平大秩空间的主要原因，这也更加论证了作者所说的“低秩”的有效性。

看到这个图表结论，你可能有一个疑惑：不是说取的是信息最丰富的8个维度，而取的是信息最丰富的64个维度吗？那么它们的前8个维度应该是一样的啊！所以随着的增加，空间重合度不是应该越来越大吗？怎么是图表的结果是越来越小呢？

这是因为“取的是信息最丰富的8个维度，而取的是信息最丰富的64个维度”这个现象，是我们的理想，而当模型真正学出来时却不是这样。模型会尽可能往信息最丰富的维度学，但不能保证取多少，最终学出来的一定就是客观存在的的top r，只能说当r取的比较小时，模型更有可能贴近真正的top r；当r取比较大时，模型学出的是部分有价值的信息和一些噪声，而这个实验则刚好论证了这一点。

如果理解了这一点，接下来我们可以更好来解读下一个实验了：模型不同的层，它们的r要如何设置呢？

5.2.3 不同层的r值设置

前面我们看到，**LoRA作用在了和上，那么对于这两个不同的矩阵，**值设置上是否也有不同的讲究呢？

为了解答这一点，作者又设计了一个实验：对三个矩阵，每个矩阵分别设置两组不同的随机种子，跑出两组不同的低秩矩阵，计算这两组低秩矩阵的Grassmann distance，结果如下：

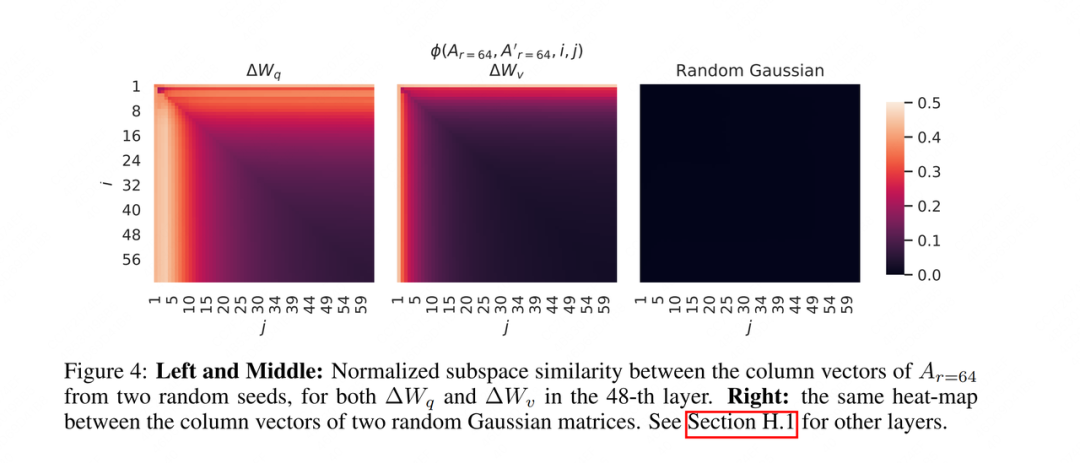
按我们之前说明的，两组并不是完美学出客观存在的的top 64维最丰富的信息，而是“部分有效的信息+一些噪声”，基于此我们不难想到：两组都能学到的信息，大概率就是有用的信息了。所以我们对这两组也做了相似度的计算，从左图中可以看出，的top 10的颜色最浅，在这以内的，可能就是较为有效的信息了。根据这样的分析结果，我们也能对模型的不同部分采用不同的秩。

5.2.4 预训练权重 VS 微调权重

之前我们说过，**预训练权重是旧知识，微调权重是新知识。所以正常来说，中应该会有一些没有关注到的部分。所以，我们也有必要论证我们训出的低秩矩阵是不是符合了这一点。**作者设计的实验结果如下：

其中表示训练出来的用低秩矩阵近似的结果，不是前文所说的客观存在。

我们来解读一下这个实验：

• 首先看表格的最下行，分别对预训练权重，增量权重计算范数，我们可以将这个指标粗略地理解为****中蕴含的全量信息量。

• 接下来，我们求指标，这里我们共有6组值：前3个来自时，矩阵的奇异值分解结果，后三个以此类推。**因此表示：把预训练权重分别投影到这三者的低秩近似特征空间中去，去计算投影过后在对应特征空间的信息量。**如果和对应特征空间越相似，则值越大。

光看概念是不是有些迷糊，那我们来找个具体指标解读一下吧：

• 首先来看61.95和21.67这一组。61.95表示预训练权重本身具有的信息量，21.67表示把投影到自己的低秩空间后的信息量（投影到低秩空间必然会产生信息损失）。

• 再来看0.32和0.02这一组。0.32表示预训练权重投影到增量权重的的低秩空间后的信息量，0.02同理类推。可以看出，含义新知识的增量权重与随机权重相比，和预训练权重还是有一定相关性的。

• 最后，我们再来看6.91和0.32。预训练权重投影到增量权重的低秩空间后，信息量从61.95降为0.32，**说明预训练权重（旧知识）和增量权重（新知识）的分布间还是存在显著差异的。**6.91表示增量权重本身的信息量。**因此21.95 = 6.91/0.32这个值，恰好能表示增量权重对预训练权重中那些没有强调的信息的放大程度。**秩越小，放大程度越明显。

好！关于LoRA的原理介绍，我们就一起学习到这里了。大家可能发现这篇文章花了比较多的篇幅再实验介绍上，一方面通过实验，可以帮助我们更好理解低秩的含义和作用；另一方面，我个人觉得LoRA实验的结果不是很好读，所以想花些时间多钻研下。那么在下一篇中，我们再来解读下LoRA的代码实现吧！

六、参考

1、https://arxiv.org/pdf/2106.09685.pdf
2、https://github.com/microsoft/LoRA
3、https://medium.com/@Shrishml/lora-low-rank-adaptation-from-the-first-principle-7e1adec71541
4、https://blog.sciencenet.cn/blog-696950-699432.html
5、https://kexue.fm/archives/9590/comment-page-1