链式二叉树的基本操作实现

news2024/11/26 0:23:46

💓博主csdn个人主页：小小unicorn
⏩专栏分类：数据结构
🚚代码仓库：小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识

链式二叉树基本操作

  • 二叉树节点设置
  • 二叉树的深度优先遍历
    • 前序遍历
    • 中序遍历
    • 后序遍历
  • 二叉树的广度优先遍历
  • 节点的个数
  • 叶子节点个数
  • 树中第K层节点的个数
  • 查找值为X的节点
  • 树的最大深度
  • 翻转二叉树
  • 判断二叉树是否为完全二叉树
  • 判断二叉树是否为对称二叉树
  • 判断二叉树是否为平衡二叉树
  • 判断二叉树是否为单值二叉树
  • 判断二叉树是另一棵树的子树
  • 判断两颗二叉树是否相同
  • 二叉树的销毁
  • 二叉树的深度遍历（接口型题目）
    • 前序遍历
    • 中序遍历
    • 后序遍历

二叉树节点设置

链式二叉树，那必须得有自己的结点类型，以下是链式二叉树结点类型的定义，为了避免过多重复的代码，下面的问题都统一使用该结点类型。

typedef char BTDataType;//结点中存储的元素类型（以char为例）

typedef struct BTNode
{
	BTDataType val;//结点中存储的元素类型
	struct BTNode* left;//左指针域（指向左孩子）
	struct BTNode* right;//右指针域（指向右孩子）
}BTNode;

二叉树的深度优先遍历

学习二叉树结构，最简单的方式就是遍历。

所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。

遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

  1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
  2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。
  3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
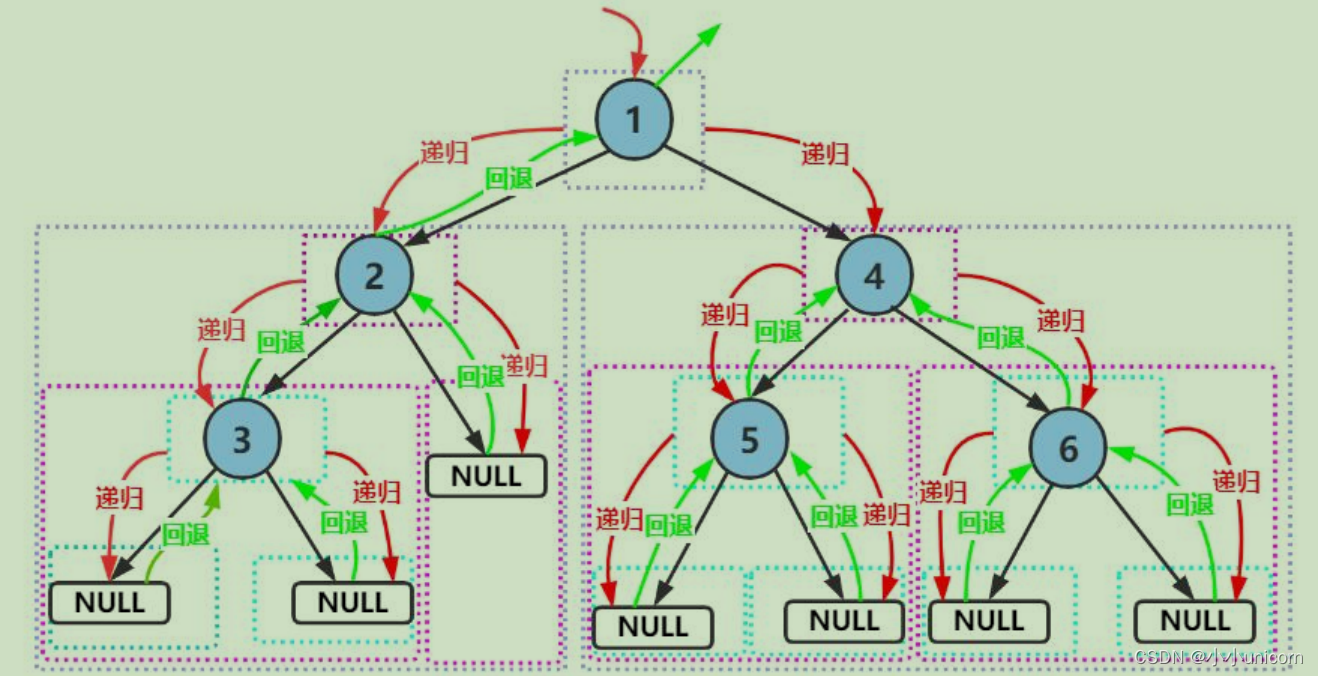
在这里插入图片描述

前序遍历

前序遍历，又叫先根遍历。
遍历顺序：根 -> 左子树 -> 右子树

//前序遍历
void BinaryPrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	//根->左子树->右子树
	printf("%c ", root->val);
	BinaryPrevOrder(root->left);
	BinaryPrevOrder(root->right);
}

中序遍历

中序遍历，又叫中根遍历。
遍历顺序：左子树 -> 根 -> 右子树

void BinaryInOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	//左子树->根->右子树
	BinaryInOrder(root->left);
	printf("%c ", root->val);
	BinaryInOrder(root->right);
}

后序遍历

后序遍历，又叫后根遍历。
遍历顺序：左子树 -> 右子树 -> 根

//后序遍历
void BinaryPostOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	//左子树->右子树->根
	BinaryPostOrder(root->left);
	BinaryPostOrder(root->right);
	printf("%c ", root->val);
}

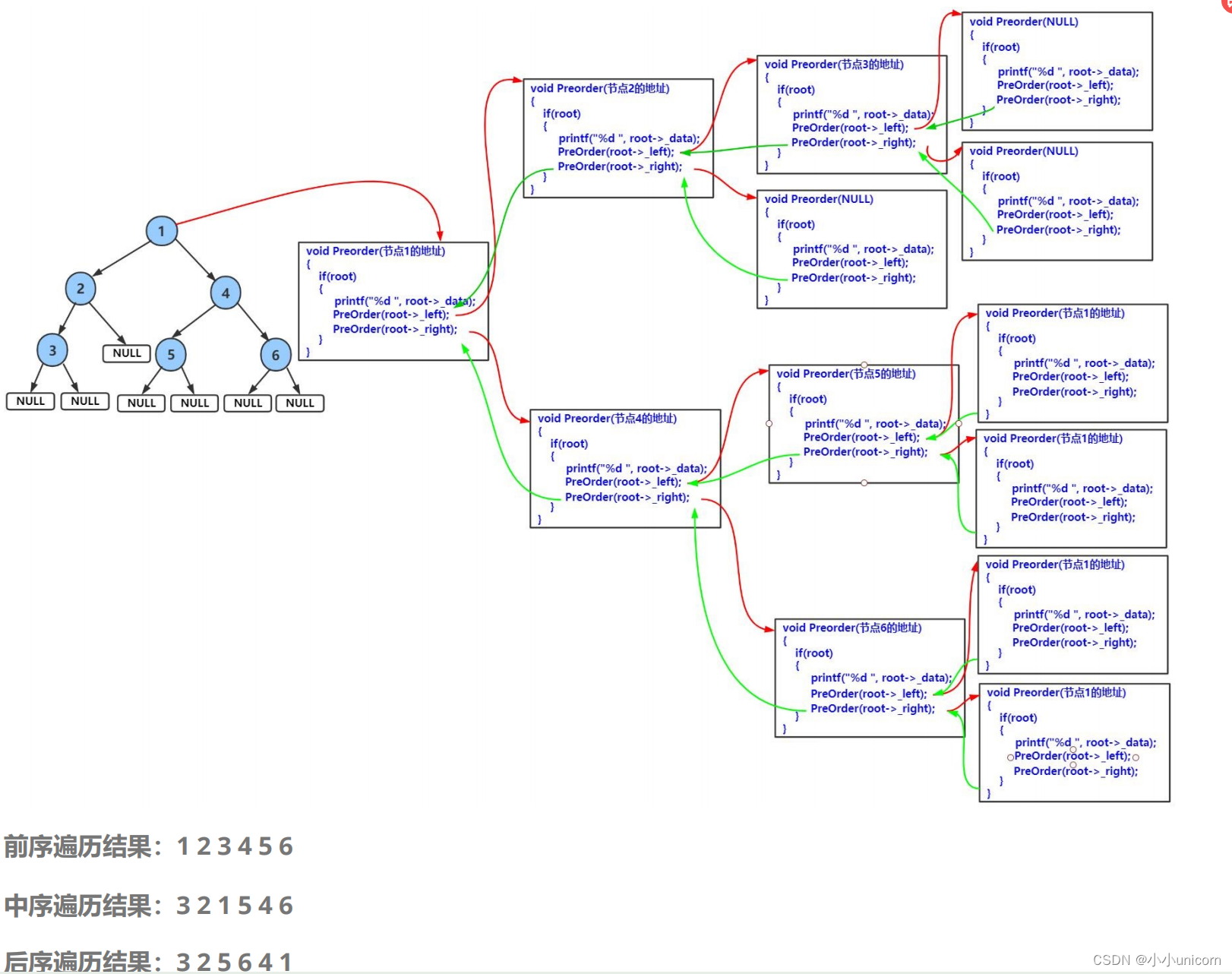
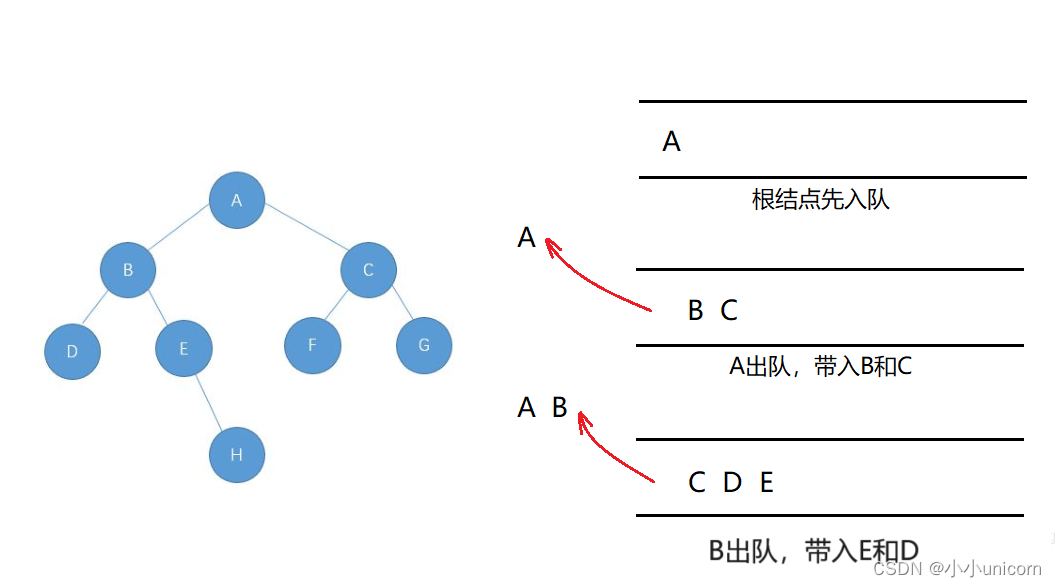
在这里插入图片描述

二叉树的广度优先遍历

层序遍历：
层序遍历，自上而下，从左往右逐层访问树的结点的过程就是层序遍历。
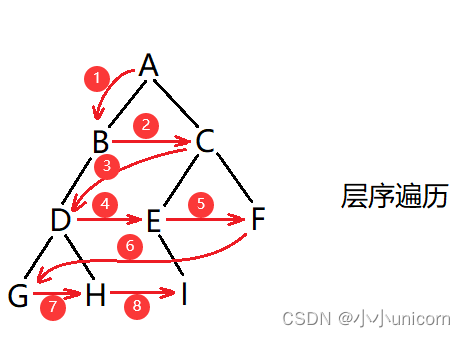
在这里插入图片描述
思路（借助一个队列）：
 1.先把根入队列，然后开始从队头出数据。
 2.出队头的数据，把它的左孩子和右孩子依次从队尾入队列（NULL不入队列）。
 3.重复进行步骤2，直到队列为空为止。
 在这里插入图片描述

//层序遍历
void BinaryLevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);//初始化队列
	if (root != NULL)
		QueuePush(&q, root);
	while (!QueueEmpty(&q))//当队列不为空时，循环继续
	{
		BTNode* front = QueueFront(&q);//读取队头元素
		QueuePop(&q);//删除队头元素
		printf("%c ", front->val);//打印出队的元素
		if (front->left)
		{
			QueuePush(&q, front->left);//出队元素的左孩子入队列
		}
		if (front->right)
		{
			QueuePush(&q, front->right);//出队元素的右孩子入队列
		}
	}
	QueueDestroy(&q);//销毁队列
}

节点的个数

求解树的结点总数时，可以将问题拆解成子问题：
 1.若为空，则结点个数为0。
 2.若不为空，则结点个数 = 左子树结点个数 + 右子树结点个数 + 1（自己）。

//结点的个数
int BinaryTreeSize(BTNode* root)
{	
	//结点个数 = 左子树的结点个数 + 右子树的结点个数 + 自己
	return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

叶子节点个数

继续将子问题拆解：
 1.若为空，则叶子结点个数为0。
 2.若结点的左指针和右指针均为空，则叶子结点个数为1。
 3.除上述两种情况外，说明该树存在子树，其叶子结点个数 = 左子树的叶子结点个数 + 右子树的叶子结点个数。

//叶子结点的个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)//空树无叶子结点
		return 0;
	if (root->left == NULL&&root->right == NULL)//是叶子结点
		return 1;
	//叶子结点的个数 = 左子树的叶子结点个数 + 右子树的叶子结点个数
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

树中第K层节点的个数

思路：
 相对于根结点的第k层结点的个数 = 相对于以其左孩子为根的第k-1层结点的个数 + 相对于以其右孩子为根的第k-1层结点的个数。
 在这里插入图片描述

//第k层结点的个数
int BinaryTreeKLevelSize(BTNode* root, int k)
{
	if (k < 1 || root == NULL)//空树或输入k值不合法
		return 0;
	if (k == 1)//第一层结点个数
		return 1;
	//相对于父结点的第k层的结点个数 = 相对于两个孩子结点的第k-1层的结点个数之和
	return BinaryTreeKLevelSize(root->left, k - 1) + BinaryTreeKLevelSize(root->right, k - 1);
}

查找值为X的节点

子问题：
 1.先判断根结点是否是目标结点。
 2.再去左子树中寻找。
 3.最后去右子树中寻找。

//查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)//空树
		return NULL;
	if (root->val == x)//先判断根结点
		return root;
	BTNode* lret = BinaryTreeFind(root->left, x);//在左子树中找
	if (lret)
		return lret;
	BTNode* rret = BinaryTreeFind(root->right, x);//在右子树中找
	if (rret)
		return rret;
	return NULL;//根结点和左右子树中均没有找到
}

树的最大深度

子问题：
 1.若为空，则深度为0。
 2.若不为空，则树的最大深度 = 左右子树中深度较大的值 + 1。

//求较大值
int Max(int a, int b)
{
	return a > b ? a : b;
}
//树的最大深度
int BinaryTreeMaxDepth(BTNode* root)
{
	if (root == NULL)//空树，深度为0
		return 0;
	//树的最大深度 = 左右子树中深度较大的值 + 1
	return Max(BinaryTreeMaxDepth(root->left), BinaryTreeMaxDepth(root->right)) + 1;
}

翻转二叉树

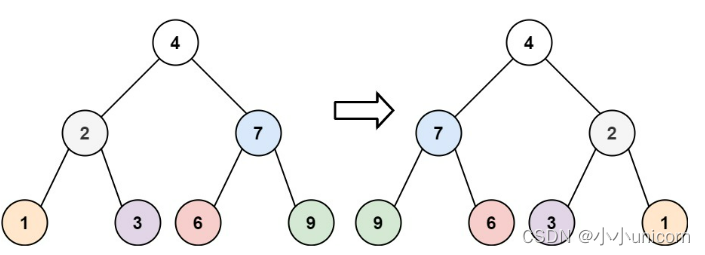
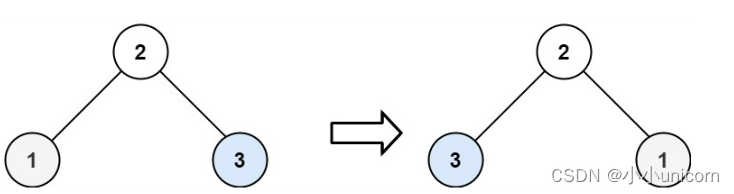
在这里插入图片描述
在这里插入图片描述

思路：
 1.翻转左子树。
 2.翻转右子树。
 3.交换左右子树的位置。

//翻转二叉树
BTNode* invertTree(BTNode* root)
{
	if (root == NULL)//根为空，直接返回
		return NULL;
	BTNode* left = invertTree(root->left);//翻转左子树
	BTNode* right = invertTree(root->right);//翻转右子树
	//左右子树位置交换
	root->left = right;
	root->right = left;
	return root;
}

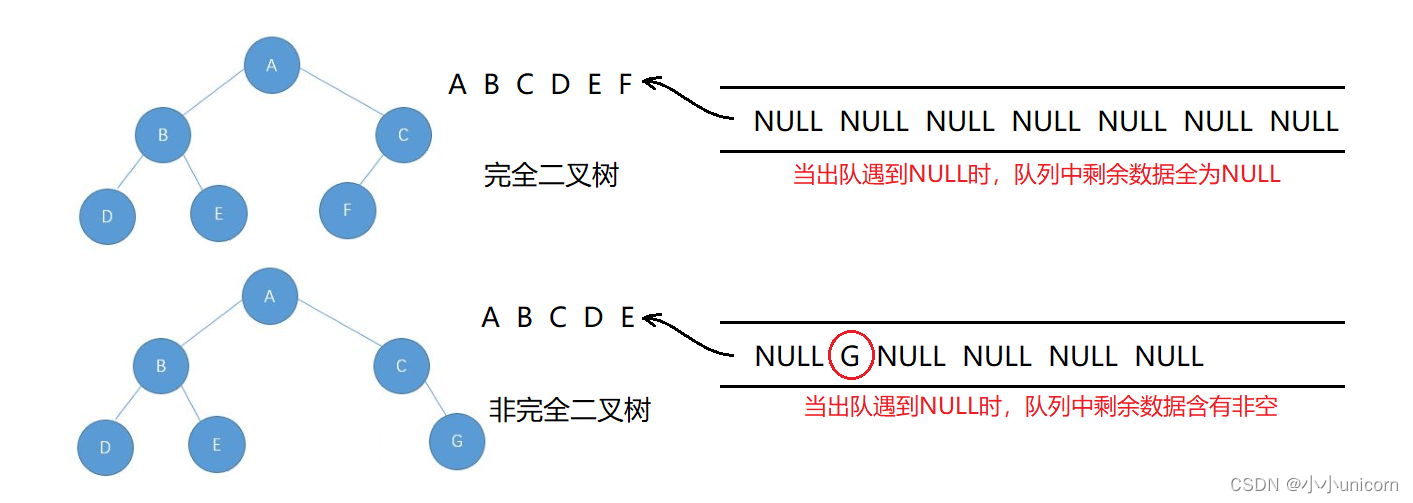
判断二叉树是否为完全二叉树

思路（借助一个队列）：
 1.先把根入队列，然后开始从队头出数据。
 2.出队头的数据，把它的左孩子和右孩子依次从队尾入队列（NULL也入队列）。
 3.重复进行步骤2，直到读取到的队头数据为NULL时停止入队列。
 4.检查队列中剩余数据，若全为NULL，则是完全二叉树；若其中有一个非空的数据，则不是完全二叉树。
 在这里插入图片描述

//判断二叉树是否是完全二叉树
bool isCompleteTree(BTNode* root)
{
	Queue q;
	QueueInit(&q);//初始化队列
	if (root != NULL)
		QueuePush(&q, root);
	while (!QueueEmpty(&q))//当队列不为空时，循环继续
	{
		BTNode* front = QueueFront(&q);//读取队头元素
		QueuePop(&q);//删除队头元素
		if (front == NULL)//当读取到空指针时，停止入队操作
			break;
		QueuePush(&q, front->left);//出队元素的左孩子入队列
		QueuePush(&q, front->right);//出队元素的右孩子入队列
	}
	while (!QueueEmpty(&q))//读取队列中剩余的数据
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)//若队列中存在非空指针，则不是完全二叉树
		{
			QueueDestroy(&q);//销毁队列
			return false;
		}
	}
	QueueDestroy(&q);//销毁队列
	return true;//若队列中全是空指针，则是完全二叉树
}

判断二叉树是否为对称二叉树

对称二叉树就是镜像对称。
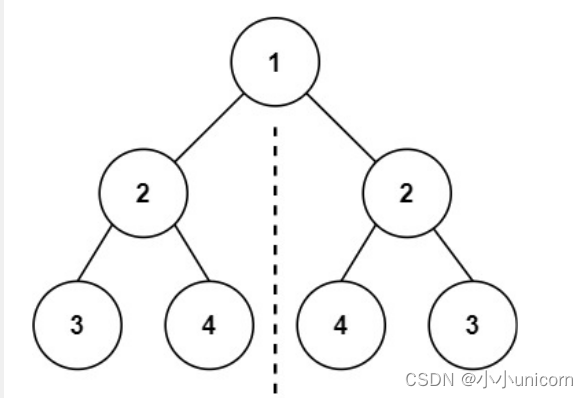
在这里插入图片描述
要判断某二叉树是否是对称二叉树，则判断其根结点的左子树和右子树是否是镜像对称即可。

因为是镜像对称，所以左子树的遍历方式和右子树的遍历方式是不同的，准确来说，左子树和右子树的遍历是反方向进行的。

//判断镜像位置是否相等
bool travel(BTNode* left, BTNode* right)
{
	if (left == NULL&&right == NULL)//红蓝轨迹同时遍历到NULL，函数返回
		return true;
	if (left == NULL || right == NULL)//红蓝指针中，一个为NULL，另一个不为NULL，即镜像不相等
		return false;
	if (left->val != right->val)//红蓝指针指向的结点值不同，即镜像不相等
		return false;
	//子问题：左子树遍历顺序：先左后右，右子树遍历顺序：先右后左。若两次遍历均成功，则是对称二叉树
	return travel(left->left, right->right) && travel(left->right, right->left);
}
//对称二叉树
bool isSymmetric(BTNode* root)
{
	if (root == NULL)//空树是对称二叉树
		return true;
	return travel(root->left, root->right);//判断镜像位置是否相等
}

判断二叉树是否为平衡二叉树

若一棵二叉树的每个结点的左右两个子树的高度差的绝对值不超过1，则称该树为平衡二叉树。
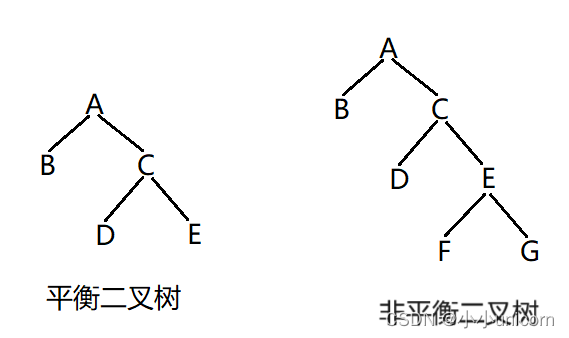
在这里插入图片描述
思路一：
继续拆分子问题：
 1.求出左子树的深度。
 2.求出右子树的深度。
 3.若左子树与右子树的深度差的绝对值不超过1，并且左右子树也是平衡二叉树，则该树是平衡二叉树。

时间复杂度O（N2）

//判断二叉树是否是平衡二叉树
bool isBalanced(BTNode* root)
{
	if (root == NULL)//空树是平衡二叉树
		return true;

	int leftDepth = BinaryTreeMaxDepth(root->left);//求左子树的深度
	int rightDepth = BinaryTreeMaxDepth(root->right);//求右子树的深度
	//左右子树高度差的绝对值不超过1 && 其左子树是平衡二叉树 && 其右子树是平衡二叉树
	return abs(leftDepth - rightDepth) < 2 && isBalanced(root->left) && isBalanced(root->right);
}

思路二：
我们可以采用后序遍历：
 1.从叶子结点处开始计算每课子树的高度。（每棵子树的高度 = 左右子树中高度的较大值 + 1）
 2.先判断左子树是否是平衡二叉树。
 3.再判断右子树是否是平衡二叉树。
 4.若左右子树均为平衡二叉树，则返回当前子树的高度给上一层，继续判断上一层的子树是否是平衡二叉树，直到判断到根为止。（若判断过程中，某一棵子树不是平衡二叉树，则该树也就不是平衡二叉树了）

bool _isBalanced(BTNode* root, int* ph)
{
	if (root == NULL)//空树是平衡二叉树
	{
		*ph = 0;//空树返回高度为0
		return true;
	}
	//先判断左子树
	int leftHight = 0;
	if (_isBalanced(root->left, &leftHight) == false)
		return false;
	//再判断右子树
	int rightHight = 0;
	if (_isBalanced(root->right, &rightHight) == false)
		return false;
	//把左右子树的高度中的较大值+1作为当前树的高度返回给上一层
	*ph = Max(leftHight, rightHight) + 1;

	return abs(leftHight - rightHight) < 2;//平衡二叉树的条件
}
//判断二叉树是否是平衡二叉树
bool isBalanced(BTNode* root)
{
	int hight = 0;
	return _isBalanced(root, &hight);
}

判断二叉树是否为单值二叉树

这个题我们可以通过判断二叉树的根与叶子是否相等来解决这个问题，注意要分三种情况：

1.如果是空树，那也是符合情况的，直接返回true。

2.首先满足左子树不为空的条件下，判断左子树的值是否与根相同，相同返回true,不相同返回false.

3.首先满足右子树不为空的条件下，判断右子树的值是否与根相同，相同返回true,不相同返回false.

bool isUnivalTree(BTNode* root)
{
   if(root==NULL)
   {
       return true;
   }
   if(root->left && root->left->val != root->val)
   {
       return false;
   }
   if(root->right && root->right->val != root->val)
   {
       return false;
   }
   return isUnivalTree(root->left)&&isUnivalTree(root->right);
}

判断二叉树是另一棵树的子树

判断 subRoot 是否是二叉树 root 的子树，即检验 root 中是否包含和 subRoot 具有相同结构和结点值的子树，其中 root 和 subRoot 均为非空二叉树。
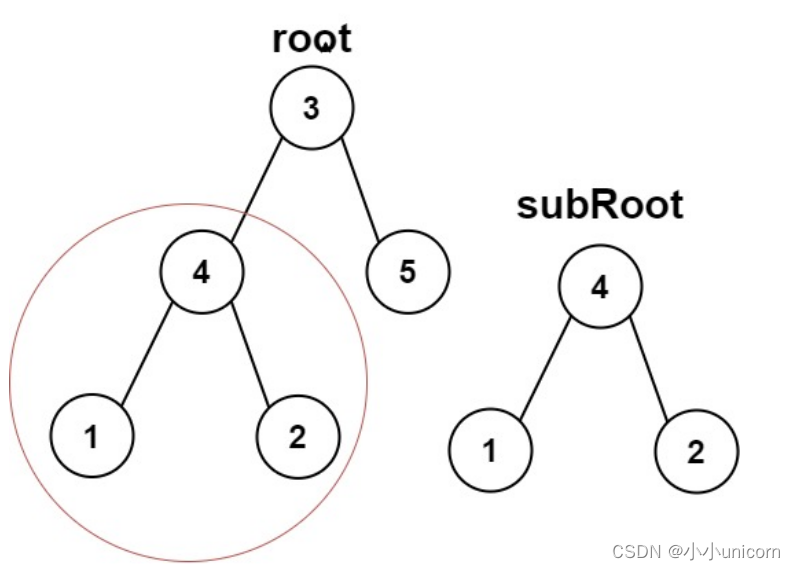
在这里插入图片描述

思路：
 依次判断以 root 中某一个结点为根的子树是否与subRoot相同。
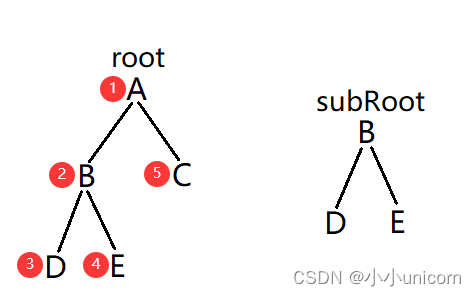
在这里插入图片描述
发现 root 中的某一个子树与 subRoot 相匹配时，便不再继续比较其他子树，所以图中只会比较到序号2就结束比较。

//比较以root和subRoot为根结点的两棵树是否相等
bool Compare(BTNode* root, BTNode* subRoot)
{
	if (root == NULL&&subRoot == NULL)//均为空树，相等
		return true;
	if (root == NULL || subRoot == NULL)//一个为空另一个不为空，不相等
		return false;
	if (root->val != subRoot->val)//结点的值不同，不相等
		return false;
	//比较两棵树的子结点
	return Compare(root->left, subRoot->left) && Compare(root->right, subRoot->right);
}
//另一个树的子树
bool isSubtree(BTNode* root, BTNode* subRoot)
{
	if (root == NULL)//空树，不可能是与subRoot相同（subRoot非空）
		return false;
	if (Compare(root, subRoot))//以root和subRoot为根，开始比较两棵树是否相同
		return true;
	//判断root的左孩子和右孩子中是否有某一棵子树与subRoot相同
	return isSubtree(root->left, subRoot) || isSubtree(root->right,subRoot);
}

判断两颗二叉树是否相同

判断两棵二叉树是否相同，也可以将其分解为子问题：
 1.比较两棵树的根是否相同。
 2.比较两根的左子树是否相同。
 3.比较两根的右子树是否相同。
 
 代码如下：

bool isSameTree(BTNode* p, BTNode* q)
{
      //都为空
      if(p==NULL&&q==NULL)
        return true;
      //其中一个为空
      if(p==NULL||q==NULL)
        return false;
      
      //都不为空
      if(p->val!=q->val)
        return false;

    return isSameTree(p->left,q->left)&&
           isSameTree(p->right,q->right);
    
}

二叉树的销毁

二叉树的销毁，与其他数据结构的销毁类似，都是一边遍历一边销毁。但是二叉树需要注意销毁结点的顺序，遍历时我们应该选用后序遍历，也就是说，销毁顺序应该为：左子树->右子树->根。
 
 我们必须先将左右子树销毁，最后再销毁根结点，若先销毁根结点，那么其左右子树就无法找到，也就无法销毁了。

//二叉树销毁
void BinaryTreeDestroy(BTNode* root)
{
	if (root == NULL)
		return;

	BinaryTreeDestroy(root->left);//销毁左子树
	BinaryTreeDestroy(root->right);//销毁右子树
	free(root);//释放根结点
}

二叉树的深度遍历（接口型题目）

接下来所要说的深度遍历与前面会有所不同，我们前面说到的深度遍历是将一棵二叉树遍历，并将遍历结果打印屏幕上（较简单）。

而下面说到的深度遍历是将一棵二叉树进行遍历，并将遍历结果存储到一个动态开辟的数组中，将数组作为函数返回值进行返回。

思路：
 1.首先计算二叉树中结点的个数，便于确定动态开辟的数组的大小。
 2.遍历二叉树，将遍历结果存储到数组中。
 3.返回数组。

前序遍历

代码：

//求树的结点个数
int TreeSize(BTNode* root)
{
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
//将树中结点的值放入数组
void preorder(BTNode* root, int* arr, int* pi)
{
	if (root == NULL)//根结点为空，直接返回
		return;
	arr[(*pi)++] = root->val;//先将根结点的值放入数组
	preorder(root->left, arr, pi);//再将左子树中结点的值放入数组
	preorder(root->right, arr, pi);//最后将右子树中结点的值放入数组
}
//前序遍历
int* preorderTraversal(BTNode* root, int* returnSize)
{
	*returnSize = TreeSize(root);//值的个数等于结点的个数
	int* arr = (int*)malloc(sizeof(int)*(*returnSize));
	int i = 0;
	preorder(root, arr, &i);//将树中结点的值放入数组
	return arr;
}

中序遍历

//求树的结点个数
int TreeSize(BTNode* root)
{
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
//将树中结点的值放入数组
void inorder(BTNode* root, int* arr, int* pi)
{
	if (root == NULL)//根结点为空，直接返回
		return;
	inorder(root->left, arr, pi);//先将左子树中结点的值放入数组
	arr[(*pi)++] = root->val;//再将根结点的值放入数组
	inorder(root->right, arr, pi);//最后将右子树中结点的值放入数组
}
//中序遍历
int* inorderTraversal(BTNode* root, int* returnSize)
{
	*returnSize = TreeSize(root);//值的个数等于结点的个数
	int* arr = (int*)malloc(sizeof(int)*(*returnSize));
	int i = 0;
	inorder(root, arr, &i);//将树中结点的值放入数组
	return arr;
}

后序遍历

//求树的结点个数
int TreeSize(BTNode* root)
{
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
//将树中结点的值放入数组
void postorder(BTNode* root, int* arr, int* pi)
{
	if (root == NULL)//根结点为空，直接返回
		return;
	postorder(root->left, arr, pi);//先将左子树中结点的值放入数组
	postorder(root->right, arr, pi);//再将右子树中结点的值放入数组
	arr[(*pi)++] = root->val;//最后将根结点的值放入数组
}
//后序遍历
int* postorderTraversal(BTNode* root, int* returnSize)
{
	*returnSize = TreeSize(root);//值的个数等于结点的个数
	int* arr = (int*)malloc(sizeof(int)*(*returnSize));
	int i = 0;
	postorder(root, arr, &i);//将树中结点的值放入数组
	return arr;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1056531.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

RabbitMQ学习笔记（消息发布确认，死信队列，集群，交换机，持久化，生产者、消费者）

RabbitMQ学习笔记（消息发布确认，死信队列，集群，交换机，持久化，生产者、消费者）

MQ&#xff08;message queue&#xff09;&#xff1a;本质上是个队列&#xff0c;遵循FIFO原则&#xff0c;队列中存放的是message&#xff0c;是一种跨进程的通信机制&#xff0c;用于上下游传递消息。MQ提供“逻辑解耦物理解耦”的消息通信服务。使用了MQ之后消息发送上游只…
阅读更多...
MySQL - mysql服务基本操作以及基本SQL语句与函数

MySQL - mysql服务基本操作以及基本SQL语句与函数

文章目录 操作mysql客户端与 mysql 服务之间的小九九了解 mysql 基本 SQL 语句语法书写规范SQL分类DDL库表查增 mysql数据类型数值类型字符类型日期类型 示例修改&#xff08;表操作&#xff09; DML添加数据删除数据修改数据 DQL查询多个字段条件查询聚合函数分组查询排序查询…
阅读更多...
【AI视野·今日Sound 声学论文速览 第十六期】Mon, 2 Oct 2023

【AI视野·今日Sound 声学论文速览 第十六期】Mon, 2 Oct 2023

AI视野今日CS.Sound 声学论文速览 Mon, 2 Oct 2023 Totally 13 papers &#x1f449;上期速览✈更多精彩请移步主页 Daily Sound Papers Improving Audio Captioning Models with Fine-grained Audio Features, Text Embedding Supervision, and LLM Mix-up Augmentation Auth…
阅读更多...
质数距离 - 如何在较合理的时间复杂度内求2e9范围内的质数

质数距离 - 如何在较合理的时间复杂度内求2e9范围内的质数

求l、r之间的质数&#xff0c;范围在2e9&#xff0c;但l、r的差值不大&#xff0c;在1e6范围内 先求出 内的质数&#xff0c;然后拿这个指数去筛[l, r]范围内的即可 #include<bits/stdc.h> #define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); #define endl \…
阅读更多...
微信开发者工具 如何设置代码的缩进

微信开发者工具 如何设置代码的缩进

最近学习小程序的时候发现微信开发工具的缩进有点问题&#xff0c;当我在pages-index-index.wxml中删除初始代码重新自己写的时候。发现里面其实是没有缩进的。 如下图&#xff1a; 然后我自己研究了一下&#xff0c;结合查了一些资料&#xff0c;总结了在微信开发者工具中设置…
阅读更多...
全网最全Java快捷键~

全网最全Java快捷键~

&#x1f308;write in front&#x1f308; &#x1f9f8;大家好&#xff0c;我是Aileen&#x1f9f8;.希望你看完之后&#xff0c;能对你有所帮助&#xff0c;不足请指正&#xff01;共同学习交流. &#x1f194;本文由Aileen_0v0&#x1f9f8; 原创 CSDN首发&#x1f412; 如…
阅读更多...
Windows11与CentOS7下配置与检测JDK与Maven环境变量

Windows11与CentOS7下配置与检测JDK与Maven环境变量

安装过程参考我这篇&#xff1a;Java开发环境的搭建与测试及相关问题的解决 JDK 一、Windows 需要配置三个系统内变量&#xff0c;分别为CLASSPATH、PATH、JAVA_HOME 。 CLASSPATH 变量 .;%JAVA_HOME%\lib\dt.jar;%JAVA_HOME%\lib\tools.jar 或者 .;%java_home%\lib;%java_…
阅读更多...
【image captioning】CaMEL: Mean Teacher Learning for Image Captioning（实现流程）

【image captioning】CaMEL: Mean Teacher Learning for Image Captioning（实现流程）

CaMEL: Mean Teacher Learning for Image Captioning（实现流程） 作者：安静到无声 个人主页 目录 CaMEL: Mean Teacher Learning for Image Captioning（实现流程）环境设置数据准备Evaluation训练程序推荐专栏参考代码: CaMEL: Mean Teacher Learning for Image Captioning.…
阅读更多...
DFS 模板：843. n-皇后问题

DFS 模板：843. n-皇后问题

n−n−皇后问题是指将 nn 个皇后放在 nnnn 的国际象棋棋盘上&#xff0c;使得皇后不能相互攻击到&#xff0c;即任意两个皇后都不能处于同一行、同一列或同一斜线上。 现在给定整数 nn&#xff0c;请你输出所有的满足条件的棋子摆法。 输入格式 共一行&#xff0c;包含整数 n…
阅读更多...
8、Nacos服务注册服务端源码分析（七）

8、Nacos服务注册服务端源码分析（七）

本文收录于专栏 Nacos 中 。 文章目录 前言确定前端路由CatalogController.listDetail()ServiceManager总结 前言 前文我们分析了Nacos中客户端注册时数据分发的设计链路&#xff0c;本文根据Nacos前端页面请求&#xff0c;看下前端页面中的服务列表的数据源于哪里。 确定前端…
阅读更多...
Complete Probability Spaces

Complete Probability Spaces

See https://math.stackexchange.com/questions/4095399/complete-probability-spaces
阅读更多...
山西电力市场日前价格预测【2023-10-03】

山西电力市场日前价格预测【2023-10-03】

日前价格预测 预测说明&#xff1a; 如上图所示&#xff0c;预测明日&#xff08;2023-10-03&#xff09;山西电力市场全天平均日前电价为278.17元/MWh。其中&#xff0c;最高日前电价为477.85元/MWh&#xff0c;预计出现在18: 45。最低日前电价为0.00元/MWh&#xff0c;预计出…
阅读更多...
概率论中的filtration中文叫什么？

概率论中的filtration中文叫什么？

1、2 - Financial Markets with Continuous Time- https://doi.org/10.1016/B978-1-78548-046-1.50002-8 2、Filtration (probability theory)-https://handwiki.org/wiki/Filtration_(probability_theory)#:~:textA%20filtration%20F%20%3D%20%28F%20i%29%20i%20%E2%88%88,…
阅读更多...
lv6 嵌入式开发-Flappy bird项目（信号机制、定时器功能实现）

lv6 嵌入式开发-Flappy bird项目（信号机制、定时器功能实现）

目录 1 信号(signal) 2 设置信号响应方式 – signal 3 设置定时器 4 示例 问题&#xff1a; getch()阻塞获取键盘按键输入&#xff0c; 怎么操作才能不影响小鸟下落和管道移动&#xff1f; getch如果阻塞&#xff0c;下面的程序都是无法执行。通过信号机制方式实现。 1 …
阅读更多...
分享46个Python源代码总有一个是你想要的

分享46个Python源代码总有一个是你想要的

分享46个Python源代码总有一个是你想要的 下载链接&#xff1a;https://pan.baidu.com/s/1oZPrXHwgzcvVpB36_dA72A?pwd8888 提取码&#xff1a;8888 chat-web项目的python后端 Django WEB商城网站项目 django-实时接口获取中国各个城市、省份、国家的新型冠状肺炎 NewsSp…
阅读更多...
多线程 - 阻塞式队列

多线程 - 阻塞式队列

阻塞队列 阻塞队列,也是一个队列 ~~ 先进先出 实际上有一些特殊的队列,不一定非得遵守先进先出的 ~~ 优先级队列(PriorityQueue) 阻塞队列,也是特殊的队列,虽然也是先进先出的,但是带有特殊的功能: 阻塞 如果队列为空,执行出队列操作,就会阻塞.阻塞到另一个线程往队列里添加元…
阅读更多...
Go：实现SMTP邮件发送订阅功能（包含163邮箱、163企业邮箱、谷歌gmail邮箱）

Go：实现SMTP邮件发送订阅功能（包含163邮箱、163企业邮箱、谷歌gmail邮箱）

需求很简单&#xff0c;就是用户输入自己的邮箱后&#xff0c;使用官方邮箱给用户发送替邮件模版 目录 前置邮件模版邮箱开启SMTP服务163邮箱163企业邮箱谷歌gmail邮箱腾讯企业邮箱-失败其他邮箱-未操作 邮件发送核心代码config.yaml配置读取邮件相关配置发送邮件 附录 前置 邮…
阅读更多...
深度学习笔记之线性代数

深度学习笔记之线性代数

深度学习笔记之线性代数 一、向量 在数学表示法中&#xff0c;向量通常记为粗体小写的符号&#xff08;例如&#xff0c;x&#xff0c;y&#xff0c;z&#xff09;当向量表示数据集中的样本时&#xff0c;它们的值具有一定的现实意义。例如研究医院患者可能面临的心脏病发作风…
阅读更多...
Ubuntu系统初始设置

Ubuntu系统初始设置

更换国内源 安装截图工具 安装中文输入法 安装QQ 参考&#xff1a; 安装双系统win10Ubuntu20.04LTS&#xff08;详细到我自己都害怕&#xff09; 引导方式磁盘分区方法UEFIGPTLegancyMBR 安装网络助手 sudo apt install net-tools 安装VS Code 使用从官网下载.deb安装包…
阅读更多...
MySQL使用Xtrabackup在线做主从

MySQL使用Xtrabackup在线做主从

1、主库上操作 1.1前提 172.16.11.2&#xff08;主库&#xff09; 172.16.11.4&#xff08;从库&#xff09; 在执行备份之前&#xff0c;确保数据库没有锁定&#xff0c;以避免备份期间的任何写操作。 确保主库上的 MySQL 服务器正在运行&#xff0c;以便备份数据的一致性。…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023