知识点

1. BFS

题目描述

思路讲解

分析一下y总的思路，也相当于做个课堂笔记吧（这也太巧妙了吧，讲解视频不到20分钟，我愣是半天没想出来

1、题目的目标

2、移动情况

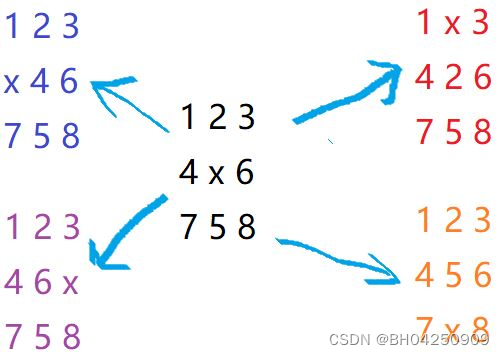
移动方式：

转移后：a = x + dx[i], b = y + dy[i].
思想：将每一种情况作为1个节点，目标情况即为终点
从初始状况移动到目标情况 —> 求最短路
3、问题

第一点：怎么表示一种情况使其能作为节点？

第二点：如何记录每一个状态的“距离”（即需要移动的次数）？

第三点：队列怎么定义，dist数组怎么定义？

4、解决方案

将 “3*3矩阵” 转化为 “字符串”
如：

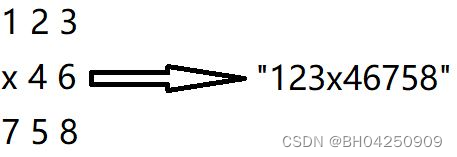
所以：

 队列可以用 queue<string>
//直接存转化后的字符串
dist数组用 unordered_map<string, int>
//将字符串和数字联系在一起，字符串表示状态，数字表示距离

5、矩阵与字符串的转换方式

代码展示

#include <iostream>
#include <algorithm>
#include <queue>
#include <unordered_map>

using namespace std;

int bfs(string start) {
    //定义目标状态
    string end = "12345678x";

    //定义队列和dist数组
    queue<string> q;
    unordered_map<string, int> d;

    //初始化队列和dist数组
    q.push(start);
    d[start] = 0; // 起点到起点的距离肯定是0

    //转移方式
    int dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1};

    while (q.size()) {  // BFS过程
        auto t = q.front();
        q.pop();

        //记录当前状态的距离，如果是最终状态则返回距离
        int distance = d[t];
        if (t == end) return distance;

        // 状态转移

        //查询x在字符串中的下标，然后转换为在矩阵中的坐标
        int k = t.find('x');
        int x = k / 3, y = k % 3;

        for (int i = 0; i < 4; i++) {
            //求转移后x的坐标
            int a = x + dx[i], b = y + dy[i];

            //当前坐标没有越界
            if (a >= 0 && a < 3 && b >= 0 && b < 3) {
                //转移x
                swap(t[k], t[a * 3 + b]);

                //如果当前状态是第一次遍历，记录距离，入队
                if (!d.count(t)) {
                    d[t] = distance + 1;
                    q.push(t);
                }

                //还原状态，为下一种转换情况做准备
                swap(t[k], t[a * 3 + b]);
            }
        }
    }
    //无法转换到目标状态，返回-1
    return -1;
}

int main() {
    string c, start;
    //输入起始状态
    for (int i = 0; i < 9; i++) {
        cin >> c;
        start += c;
    }

    cout << bfs(start) << endl;

    return 0;
}