



参考代码:
未优化的代码:
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int n=nums.size();
int sum=0;
for(const auto& e:nums)
{
sum+=e;
}
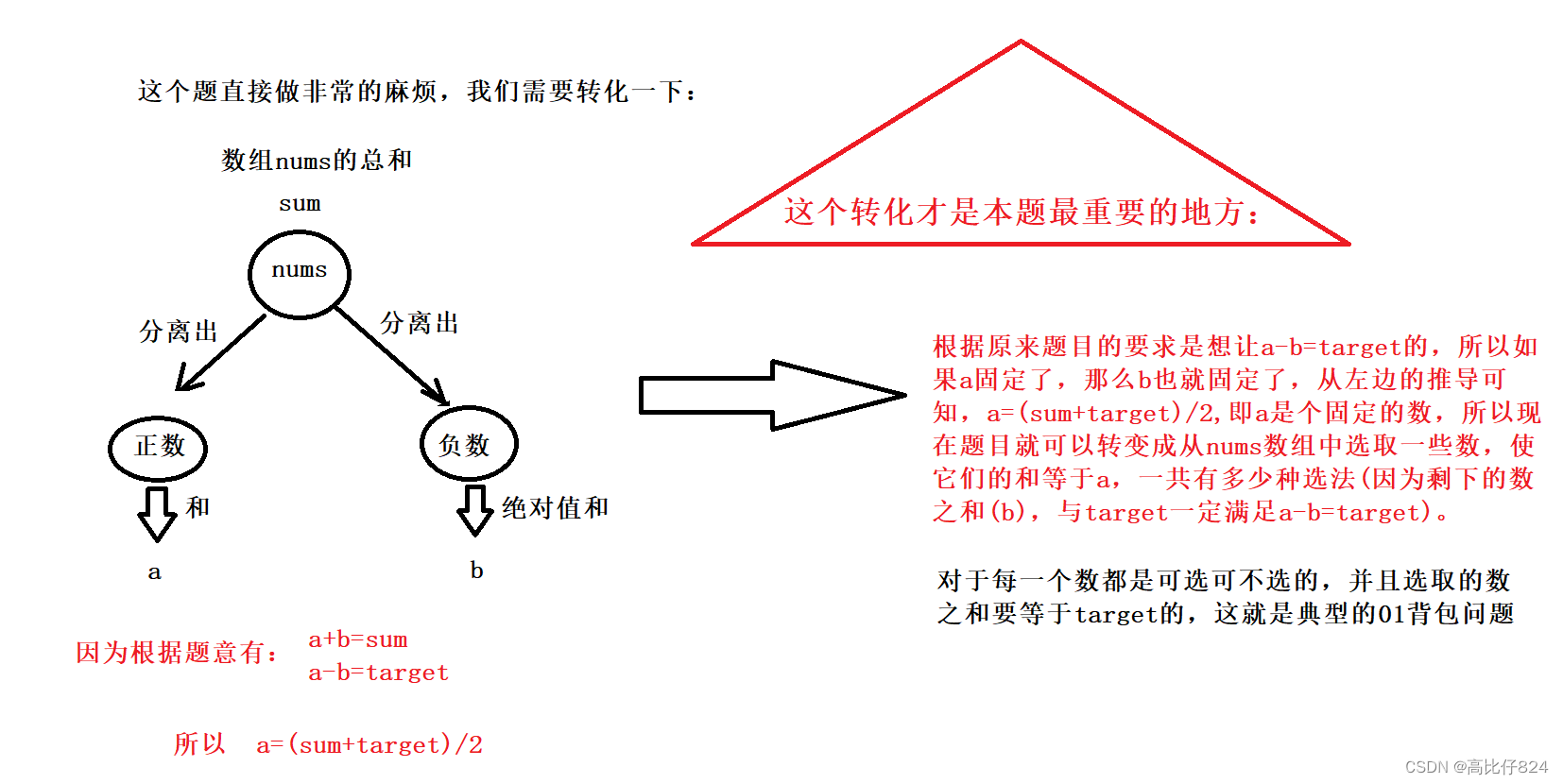
//aim+b=sum
//aim-b=target
//aim=(sum+target)/2
int aim=(sum+target)/2;
//aim是从nums中找出来的一些数的和,因为
//nums数组都是非负整数,所以如果aim<0,
//那么不可能从nums数组中凑出来aim;
//另外如果(sum+target)是一个奇数,
//即我们要找的aim=(sum+target)/2不存在,
//所以数组中也不可能找到一些数求和等于不存
//在的数,所以这两种情况直接返回0即可
if(aim<0||(sum+target)%2==1)
{
return 0;
}
//多开一行,多开一列
vector<vector<int>> dp(n+1,vector<int>(aim+1));
//初始化第一行,只需要把dp[0][0]初始化成1即可,其它的
//dp[0][j]等于0
dp[0][0]=1;
//第一列无需初始化
//填表
for(int i=1;i<=n;i++)
{
//第一列是在填表时填写,所以这里一定要从0开始
for(int j=0;j<=aim;j++)
{
//状态转移方程
dp[i][j]=dp[i-1][j];
if(j>=nums[i-1])
{
dp[i][j]+=dp[i-1][j-nums[i-1]];
}
}
}
//根据状态表示确定返回值
return dp[n][aim];
}
};优化后的代码:
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int n=nums.size();
int sum=0;
for(const auto& e:nums)
{
sum+=e;
}
//aim+b=sum
//aim-b=target
//aim=(sum+target)/2
int aim=(sum+target)/2;
//aim是从nums中找出来的一些数的和,因为
//nums数组都是非负整数,所以如果aim<0,
//那么不可能从nums数组中凑出来aim;
//另外如果(sum+target)是一个奇数,
//即我们要找的aim=(sum+target)/2不存在,
//所以数组中也不可能找到一些数求和等于不存
//在的数,所以这两种情况直接返回0即可
if(aim<0||(sum+target)%2==1)
{
return 0;
}
//多开一行,多开一列
vector<int> dp(aim+1);
//初始化第一行,只需要把dp[0][0]初始化成1即可,其它的
//dp[0][j]等于0
dp[0]=1;
//第一列无需初始化
for(int i=1;i<=n;i++)
{
//第一列是在填表时填写,所以这里一定要从0开始
for(int j=aim;j>=nums[i-1];j--)
{
//状态转移方程
dp[j]+=dp[j-nums[i-1]];
}
}
//根据状态表示确定返回值
return dp[aim];
}
};
你学会了吗???




![[C++随笔录] stack queue模拟实现](https://img-blog.csdnimg.cn/3d883dbfef3543dd8e6ec2eb3380b7fe.png)