二叉树的常见操作

news2024/11/30 14:51:42

二叉树的常见操作

注：二叉树的结构如下：

typedef char BinaryTreeDataType;
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BinaryTreeDataType data;
}BTNode;

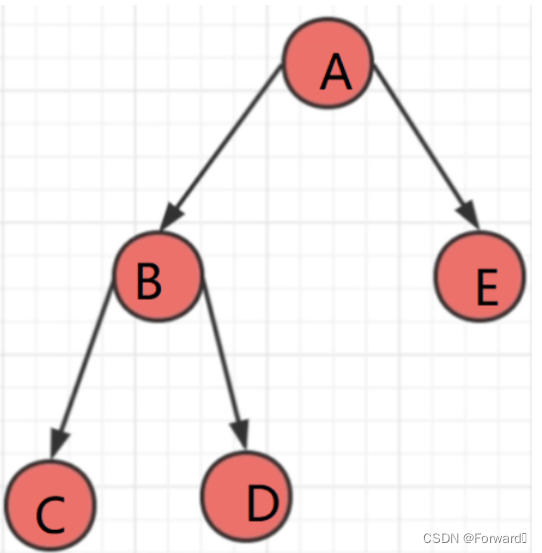
以下所有操作都以下面的树为例：

1. 求各类节点个数

1.1. 求二叉树的节点个数

错误写法1

int TreeSize(BTNode* root)
{
	static int size = 0;		//定义静态变量（也可以是全局变量），确保每一次调用函数size不会清零
	if (!root)
		return size;
	//利用前序遍历的方式计算总结点数
	size++;					
	TreeSize(root->left);
	TreeSize(root->right);
	return size;
}

计算一棵树时好像结果也没有问题：

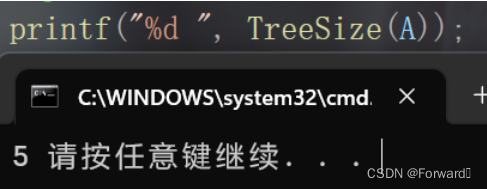
但计算两棵树的总结点时，却会出现以下情况：

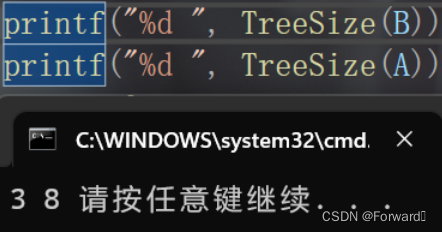
我们可以看到B这棵树的节点数确实是3，但A这棵树的节点怎么就为8了呢。原来，我们将size定义为了静态变量，当计算完B这棵树的节点再调用函数计算A树的结点树，size的大小已经为3了，这样最后得到的size就为8，显然错误。

错误写法2

那，我们将size变为全局变量并每次调用函数前将size归零不就行了吗？

int size = 0;
int TreeSize(BTNode* root)
{
   if (!root)
   	return size;
   size++;
   TreeSize(root->left);
   TreeSize(root->right);
   return size;
}

可以得到如下结果：

这么做好像是可以，但如果考虑到多线程的情况，如果两个线程同时调用这个函数，那size的值必定会被改变，因此将size定义为静态变量是行不通的

正确写法

遍历思想
void TreeSize(BTNode* root,int *size)		//因为要对size的值进行修改，因此要传地址
{
   if (!root)
   	return;
   (*size)++;
   TreeSize(root->left,size);
   TreeSize(root->right,size);
   return;
}

可以发现，结果正确：

分治思想

  • 将大问题分解成多个小问题。举个例子：树A的左子树是树B，右子树是树E，此时size为3，树B的左子树是树C，右子树是树D，此时size为5，C、D、E的左右子树都为空树，因此size为5

  • 采用了后序遍历的思想，先求左右子树的节点个数，再求根节点的节点个数

int TreeSize(BTNode* root)
{
	return  root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
    //如果为空树，则返回0，如果不为空树，则先对左子树进行递归操作，再对右子树进行递归操作，递归完成后，返回1，因为这棵树不是空树
}

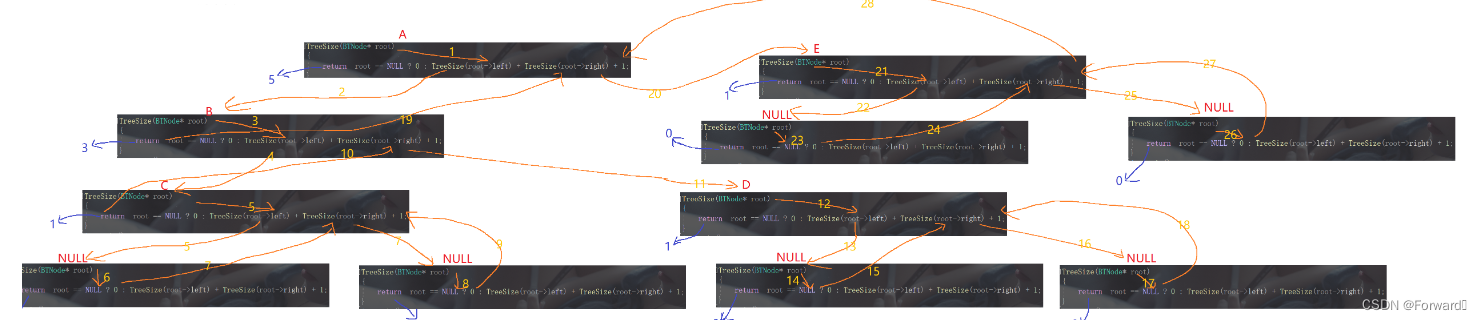
基本过程：

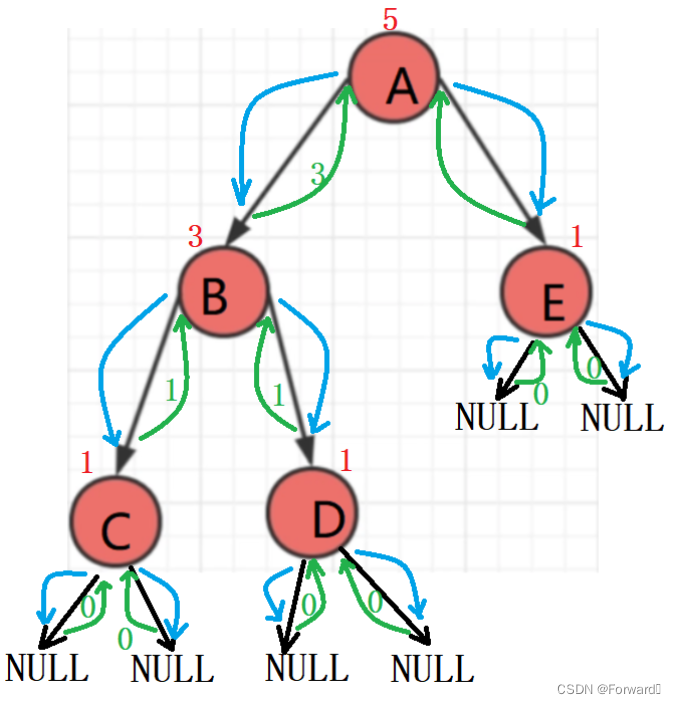
递归分解图

1.2 求二叉树叶子节点的个数

叶子节点即度为零的节点，满足的条件即：

assert(root);
root->left == NULL && root->right == NULL;

知道了这一基本常识，我们就可以利用后序遍历的思想来求得一棵二叉树叶子节点的个数了：

int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;

	return (root->left == NULL && root->right == NULL) ? 1 : BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

基本过程：

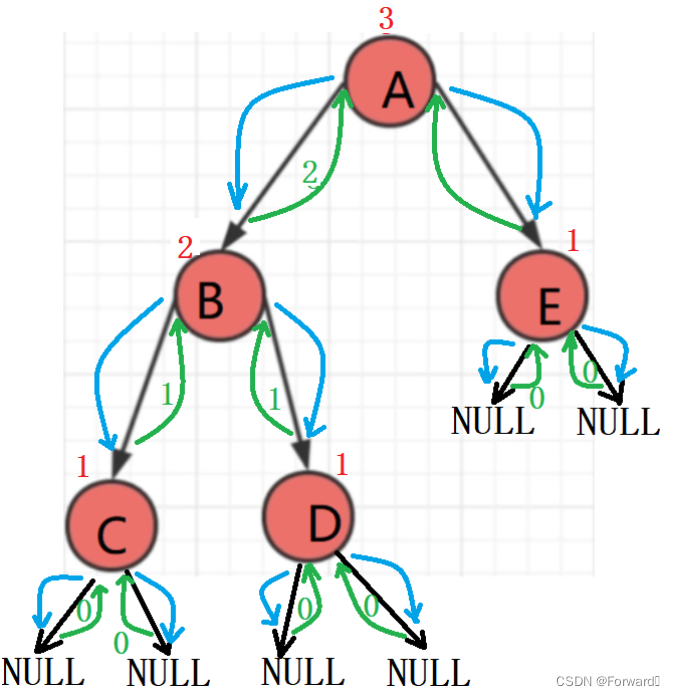
1.3 求第k层节点的个数

​ 我们将整数k也纳入函数形参，则函数原型为：

int BinaryTreeLevelKSize(BTNode* root, int k)

这里的第k层，即相较于根节点的第k层；即相较于第二层的（k-1）层；即相较于第三层的（k-2）层；即相较于第n层的（k-n+1）层，n为当前的层数。因此，当k-n+1 = 1，即k = n时，第k层节点的个数就是第n层节点的个数。

所以，要得到第k层节点的个数，只需要利用递归的思想，每一次递归都将k减一，当k == 1时，即到达第k层，节点数加1。

int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
		return 0;

	if (k == 1)
		return 1;

	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

2. 通过前序遍历序列和#号创建二叉树

题录描述：

编写一个函数，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树。例如如下的先序遍历字符串：ABC##DE#G##F###其中“#”表示空格，空格字符代表空树NULL

由于要利用一个字符串数组来构造一棵二叉树，为了能够方便读取数组的元素，作为函数参数，除了要将字符串传入，还应该传入一个指针，方便定位数组位置：

BTNode* BinaryTreeCreate(BTDataType* a, int* pi)

这里我们要用前序遍历的思想，先创建二叉树的根节点，再递归创建二叉树的左右子树：

BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{
	if (a[*pi] == '#')
	{	
		(*pi)++;
		return NULL;
	}

    //创建节点
	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	if (NULL == root)
	{
		perror("malloc");
		exit(-1);
	}

	root->data = a[*pi];
	(*pi)++;
	root->left = BinaryTreeCreate(a, pi);
	root->right = BinaryTreeCreate(a, pi);

	return root;
}

基本过程：

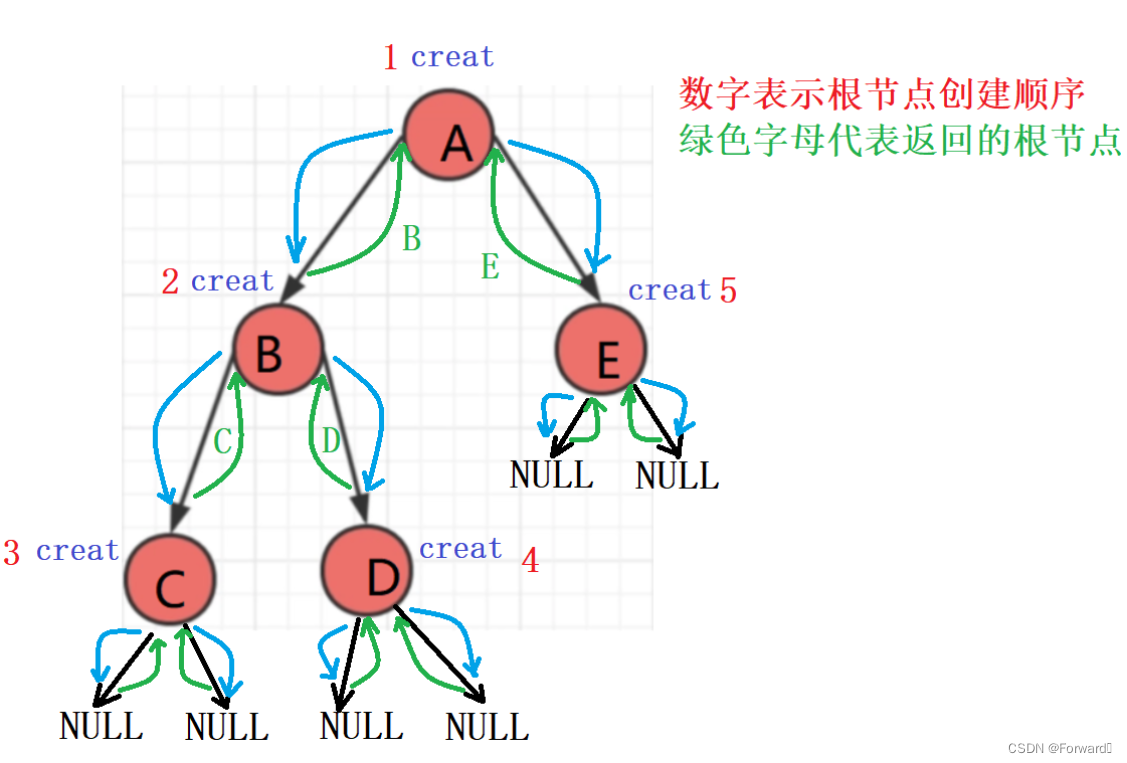
3. 查找二叉树值为x的节点，并返回该节点

利用前序遍历的思想，先判断根节点的的值是否为x，如果是，则直接返回根节点即可，否则再遍历左右子树继续查找

需要注意，利用递归查找左右子树是否有满足条件的节点时，应该对返回值进行记录，如果找到了直接返回找到的节点即可，不用再继续遍历。

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
    //先判断根节点
	if (root == NULL)
		return NULL;
	
	if (root->data == x)
		return root;

	BTNode* ret = NULL;	//用来记录返回值
    
    //判断左子树是否有符合条件的节点
	ret = BinaryTreeFind(root->left, x);
	if (ret)	//如果找到了，直接返回
		return ret;
    
    //判断右子树是否有符合条件的节点
	ret = BinaryTreeFind(root->right, x);
	if (ret)	//如果找到了，直接返回
		return ret;
	
    //如果都没找到，那么返回空
    return NULL;
}

4. 判断一棵树是否为完全二叉树

我们先来看一棵完全二叉树和一棵非完全二叉树：

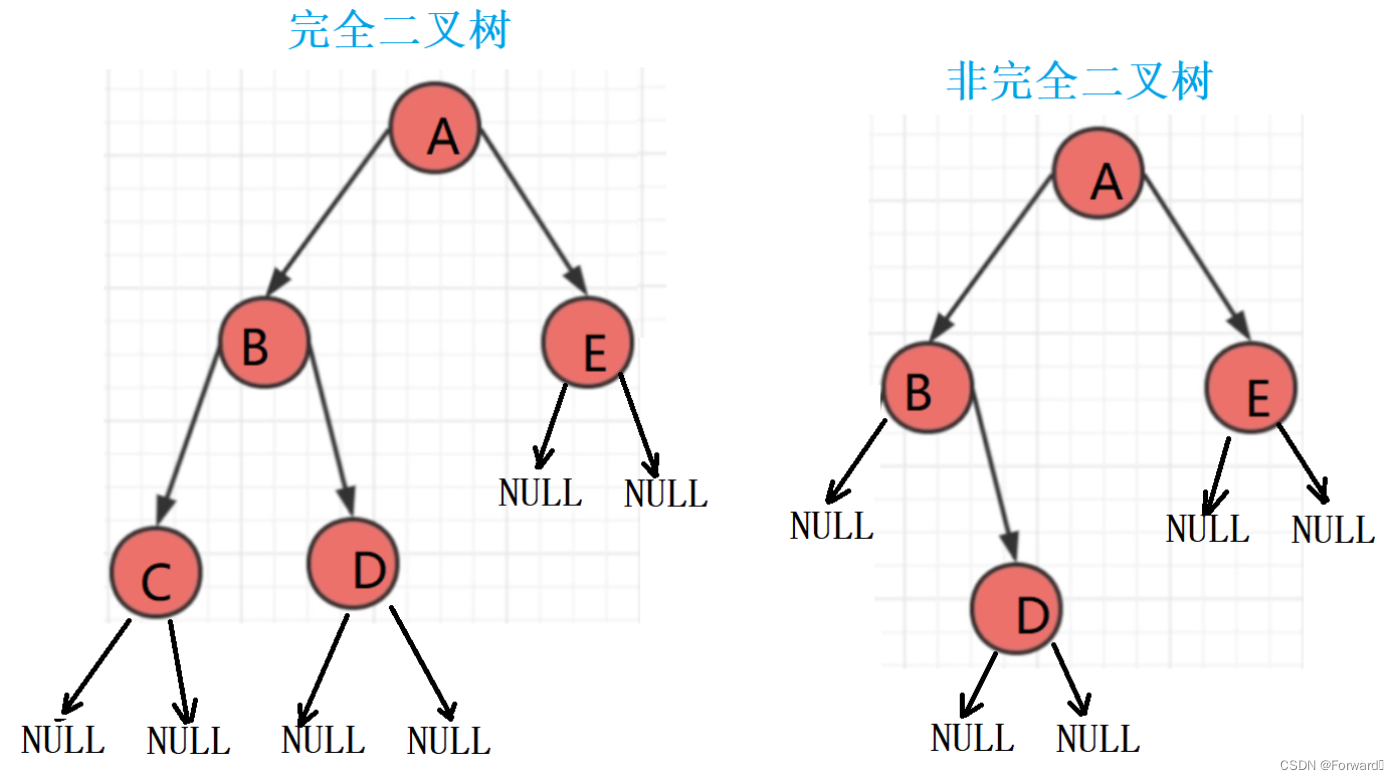
我们再来看看这两棵树的层序遍历序列：

完全二叉树：A B E C D NULL NULL NULL NULL NULL NULL

非完全二叉树：A B E NULL D NULL NULL NULL NULL

可以发现完全二叉树的层序遍历序列的空树都是连续的，而非完全二叉树的层序遍历序列的空树不是连续的，我们可以利用这一性质来判断一棵树是不是完全二叉树

注：如果对于二叉树的层序遍历操作不太了解，建议先看看👉二叉树层序遍历

/*
	QueueInit 表示初始化队列
	QueuePush 表示入队
	QueuePop 表示出队
	QueueEmpty 表示判断队列是否为空，如果为空返回true
	QueueFront 表示返回队头元素
*/
bool BinaryTreeComplete(BTNode* root)
{
	if (root == NULL)
		return true;

	Queue* q = (Queue*)malloc(sizeof(Queue));
	QueueInit(q);

	QueuePush(q, root);

    //层序遍历队列的节点
	while (!QueueEmpty(q))
	{
		BTNode* front = QueueFront(q);
		QueuePop(q);
		
        //如果此时队头元素为空，那么就可以退出循环，看队列剩余元素是否含有非空节点
		if (front == NULL)
			break;

		QueuePush(q, front->left);
		QueuePush(q, front->right);
	}
	
    //看队列剩余元素是否含有非空节点
	while (!QueueEmpty(q))
	{
		BTNode* front = QueueFront(q);
		QueuePop(q);
		
     	//如果含有非空节点，就说明不是完全二叉树
		if (front != NULL)
		{
            //销毁队列
			QueueDestroy(q);

			return false;
		}
	}

	QueueDestroy(q);

	return true;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1054795.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

PHP8中final关键字的应用-PHP8知识详解

PHP8中final关键字的应用-PHP8知识详解

在PHP8中，final的中文含义是最终的、最后的意思。被final修饰过的类和方法就是“最终的版本”。 如果关键字final放在类的前面，则表示该类不能被继承。 如果关键字final放在方法的前面，则表示该 方法不能被重新定义。 如果有一个类的格式为…
阅读更多...
ili9431液晶 tft_espi图形库演示 时钟、天气、滚动、气象图标

ili9431液晶 tft_espi图形库演示 时钟、天气、滚动、气象图标

米思齐tft_spi模块库演示程序。心知天气、阿里云时钟、WiFi信号强度检测、1分钟滚屏、更新天气时间为15分钟、加入天气图标。更新天气次数。断网检测 。此程序为tft_eSPI图形库演示、如感觉好可以自行优化。 ili9431tft_espi库是用于ESP32和ESP8266芯片的TFT LCD驱动程序库&am…
阅读更多...
C++基础_Day02

C++基础_Day02

文章目录 四、流程控制语句4.1 选择结构4.1.1 if语句 4.1.2 三目运算符4.1.3 switch语句注意事项 4.1.4 if和switch的区别【CHAT】4.2 循环结构4.2.1 while循环语句4.2.2 do...while循环语句 4.2.3 for循环语句九九乘法表 4.3 跳转语句4.3.1 break语句4.3.2 continue语句4.3.3 …
阅读更多...
京东优惠券哪里找到如何领取内部隐藏优惠券怎么使用京东优惠券？

京东优惠券哪里找到如何领取内部隐藏优惠券怎么使用京东优惠券？

京东优惠券是指通过草柴APP查询要购买京东商品的大额隐藏优惠券，找到后点击进入领取京东优惠券，然后再京东购物可享受领券更便宜的购物方式。 京东优惠券哪里领取内部隐藏优惠券怎么使用？ 1、打开京东APP挑选要购买的商品，并点击…
阅读更多...
C++简单实现AVL树

C++简单实现AVL树

目录 一、AVL树的概念 二、AVL树的性质 三、AVL树节点的定义 四、AVL树的插入 4.1 parent的平衡因子为0 4.2 parent的平衡因子为1或-1 4.3 parent的平衡因子为2或-2 4.3.1 左单旋 4.3.2 右单旋 4.3.3 先左单旋再右单旋 4.3.4 先右单旋再左单旋 4.4 插入节点完整代码…
阅读更多...
C++指针常量，常量指针以及， 引用和指针的区别

C++指针常量，常量指针以及， 引用和指针的区别

const修饰指针有三种情况 1. const修饰指针 --- 常量指针 2. const修饰常量 --- 指针常量 3. const即修饰指针，又修饰常量 c int main() {int a 10;int b 10;//const修饰的是指针，常量指针，指针指向可以改，指针指向的值不…
阅读更多...
linux——进程间通信——管道

linux——进程间通信——管道

✅<1>主页&#xff1a;&#xff1a;我的代码爱吃辣 &#x1f4c3;<2>知识讲解&#xff1a;Linux——进程间通信——管道通信 ☂️<3>开发环境&#xff1a;Centos7 &#x1f4ac;<4>前言&#xff1a;进程间通信&#xff08;InterProcess Communication&…
阅读更多...
Linux 文件上传、下载

Linux 文件上传、下载

1、通过FinalShell工具虚拟机进行数据交换 在FinalShell软件的下方窗体中&#xff0c;提供了Linux的文件系统视图&#xff0c;可以方便的&#xff1a; 浏览文件系统&#xff0c;找到合适的文件&#xff0c;右键点击下载&#xff0c;即可传输到本地电脑 浏览文件系统&#xff0…
阅读更多...
密码技术 (5) - 数字签名

密码技术 (5) - 数字签名

一. 前言 前面在介绍消息认证码时&#xff0c;我们知道消息认证码虽然可以确认消息的完整性&#xff0c;但是无法防止否认问题。而数字签名可以解决否认的问题&#xff0c;接下来介绍数字签名的原理。 二. 数字签名的原理 数字签名和公钥密码一样&#xff0c;也有公钥和私钥&am…
阅读更多...
网站使用SSL证书是趋势吗？

网站使用SSL证书是趋势吗？

随着互联网技术的不断发展&#xff0c;网络安全问题日益受到重视。其中&#xff0c;SSL证书作为网站安全的基石&#xff0c;其重要性不言而喻。SSL证书能够加密网站与用户之间的通信&#xff0c;保护用户隐私&#xff0c;防止信息被窃取和篡改。因此&#xff0c;越来越多的网站…
阅读更多...
10.1作业

10.1作业

#include <stdio.h> #include <string.h> #include <stdlib.h> /** function:* 创建一个双向链表&#xff0c;将26个英文字母通过头插的方式插入&#xff0c;通过为尾删的方式读取并删除* param [ in] * param [out] * return */ typedef struct double…
阅读更多...
ECharts多个数据视图进行自适应大小的解决方案

ECharts多个数据视图进行自适应大小的解决方案

项目场景&#xff1a; 在制作数据视图时经常会遇到多个数据视图的情况&#xff0c;在多个数据视图的情况下做自适应是比较麻烦的&#xff0c;这里就详细的分析一下该如何去制作&#xff0c;分享一下我的解决办法及思路。 定义 DOM 容器 这里需要注意一个地方&#xff0c;在定…
阅读更多...
《Jetpack Compose从入门到实战》第八章 Compose页面 导航

《Jetpack Compose从入门到实战》第八章 Compose页面 导航

添加依赖&#xff1a;implementation “androidx.navigation:navigation-compose:$nav_version” Navigation for Compose class MainActivity : AppCompatActivity() {var theme: BloomTheme by mutableStateOf(BloomTheme.LIGHT)override fun onCreate(savedInstanceState:…
阅读更多...
Vue3核心源码解析 (一) ： 源码目录结构

Vue3核心源码解析 (一) ： 源码目录结构

通过软件框架阅读源码可以对框架本身运行机制进行学习&#xff0c;更能了解框架的API设计、原理及流程、设计思路&#xff1b;我们要知其然&#xff0c;更知其所以然。 Vue 3的源码相对于Vue 2版本有了较大程度的改变&#xff0c;采用Monorepo规范的目录结构&#xff0c;同时使…
阅读更多...
JavaScript——APIs

JavaScript——APIs

复习&#xff1a; splice() 方法用于添加或删除数组中的元素。 **注意&#xff1a;**这种方法会改变原始数组。 删除数组&#xff1a; splice(起始位置&#xff0c; 删除的个数) 比如&#xff1a;1 let arr [red, green, blue] arr.splice(1,1) // 删除green元素 consol…
阅读更多...
【ArcGIS Pro二次开发】(69)：使用MapTool实现隐藏和隔离图层

【ArcGIS Pro二次开发】(69)：使用MapTool实现隐藏和隔离图层

一、MapTool简介 在ArcGIS Pro SDK中&#xff0c;MapTool是一个重要的组件&#xff0c;用于自定义地图操作工具&#xff0c;使用户能够在ArcGIS Pro中执行特定的地图交互操作。 在VS中添加新项&#xff0c;可以找到ArcGIS Pro 地图工具&#xff0c;即为MapTool。 新建后打开c…
阅读更多...
全连接网络实现回归【房价预测的数据】

全连接网络实现回归【房价预测的数据】

也是分为data&#xff0c;model&#xff0c;train&#xff0c;test import torch import torch.nn as nn import torch.nn.functional as F import torch.optim as optimclass FCNet(nn.Module):def __init__(self):super(FCNet,self).__init__()self.fc1 nn.Linear(331,200)s…
阅读更多...
​萝卜刀《乡村振兴战略下传统村落文化旅游设计》许少辉八一新书

​萝卜刀《乡村振兴战略下传统村落文化旅游设计》许少辉八一新书

​萝卜刀《乡村振兴战略下传统村落文化旅游设计》许少辉八一新书 ​萝卜刀《乡村振兴战略下传统村落文化旅游设计》许少辉八一新书
阅读更多...
mysql join语句优化实战

mysql join语句优化实战

生产环境的大表join语句性能经常很差。这里给出大表join语句的优化思路。 准备材料 两张表&#xff0c;t1表N行&#xff0c;t2表M行 CREATE TABLE identity.t1 (id INT NOT NULL COMMENT Id,a INT NULL,PRIMARY KEY (id));CREATE TABLE identity.t2 (id INT NOT NULL COMMEN…
阅读更多...
react create-react-app 配置less

react create-react-app 配置less

环境信息&#xff1a; create-react-app:v5 react:18.2.0 node:18.16.0 如果你不必须使用 less 建议直接使用scss。 因为less配置会遇到很多问题。 配置less过程&#xff1a; 如果你只需要 sass的话&#xff0c;就可以直接使用sass。因为默认配置了scss。 npm、yarn、cnpm、…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023