leetCode 309.买卖股票的最佳时机含冷冻期动态规划 + 滚动数组

news2025/1/4 17:34:19

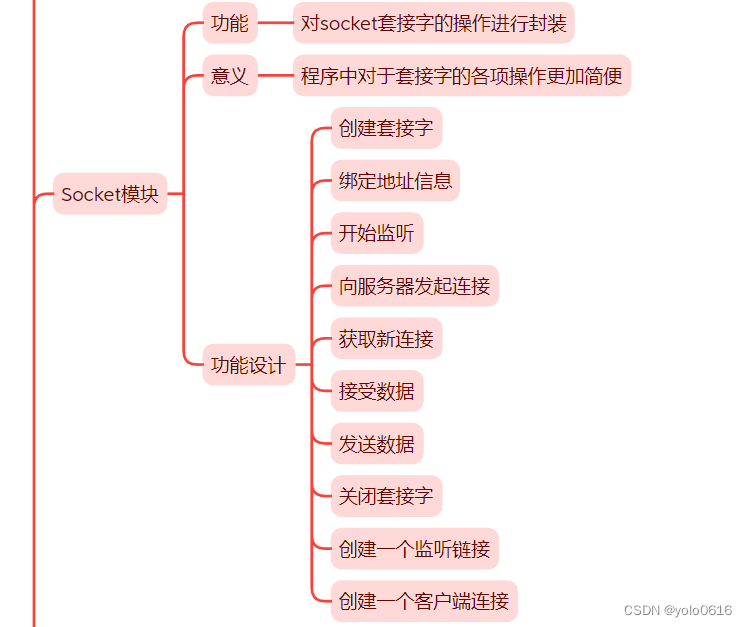
309. 买卖股票的最佳时机含冷冻期 - 力扣（LeetCode）

给定一个整数数组prices，其中第 prices[i] 表示第 i 天的股票价格。设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入: prices = [1,2,3,0,2]
输出: 3 
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]

示例 2:

输入: prices = [1]
输出: 0

>>思路和分析

相对于动态规划：leetCode 122.买卖股票的最佳时机 II ，本题加上了一个冷冻期

在leetCode 122.买卖股票的最佳时机 II中有两个状态，持有股票后的最多现金，和不持有股票的最多现金

>>动规五部曲

1.确定dp数组以及下标的含义

dp[i][j]，第 i 天状态为 j ，所剩的最多现金为 dp[i][j]

>>四个状态分析：

状态一：持有股票状态（今天买入股票，或者是之前就买入了股票，之后一直没有操作，一直持有）
不持有股票状态，可以分为两种卖出股票状态
- 状态二：保持卖出股票的状态（两天前就卖出了股票，度过一天冷冻期。或者前一天就是卖出过股票状态，一直没有操作）
- 状态三：今天卖出股票
状态四：今天为冷冻期状态，但冷冻期状态不可持续，只有一天！

问题(O_O)?思考:“今天卖出股票”，在本题中为什么要单独列出这个状态呢？

是因为本题中有冷冻期，而冷冻期的前一天，只能是“今天卖出股票”状态，如果是“不持有股票状态”就会很模糊，这是因为它不一定是卖出股票的操作。

2.确定递推公式

① 状态一（持有股票状态）: dp[i][0]，有两个具体操作：

操作一：前一天就是持有股票状态（状态一），dp[i][0] = dp[i-1][0];
操作二：今天买入了，有两种情况
- 前一天是保持卖出股票的状态（状态二）,dp[i-1][1]-prices[i];
- 前一天是冷冻期（状态四），dp[i-1][3] - prices[i];

那么dp[i][0] = max(dp[i-1][0],dp[i-1][1]-prices[i],dp[i-1][3]-prices[i]);

② 状态二（保持卖出股票的状态）：dp[i][1]，有两个具体操作：

操作一：前一天就是保持卖出股票的状态（状态二），dp[i][1] = dp[i-1][1];
操作二：前一天就是冷冻期（状态四），dp[i][1] = dp[i-1][3];

那么dp[i][1] = max(dp[i-1][1],dp[i-1][3]);

③ 状态三（今天卖出股票）：dp[i][2]，只有一个操作：

昨天一定是持有股票状态（状态一），那么今天才可以卖出

那么dp[i][2] = dp[i-1][0] + prices[i];

④ 状态四（冷冻期状态）：dp[i][3]，只有一个操作：

昨天一定是卖出了股票（状态三），那么今天我就进入了冷冻期状态

那么dp[i][3] = dp[i-1][2];

综上分析，递推代码如下：

dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];

3.dp数组初始化

第 0 天的初始化：

① 状态一（持有股票状态）：dp[0][0] = -prices[0]，表示一定是当天买入股票

② 状态二（保持卖出股票状态）：很难从其定义来明确应初始为多少，那么此种情况我们就看递推公式需要给它初始成什么数值。例如：i = 1，在第 i 天买入股票，那么递归公式中需要计算

dp[i-1][1] - prices[i],即dp[0][1]-prices[1]

那么dp[0][1]只能初始为0，若初始为其他数值，则第1天买入股票后手里所剩的现金就不对了

③ 状态三（今天卖出股票），同上分析，dp[0][2]也初始化为0

④ 状态四（冷冻期状态），同上分析，dp[0][3]也初始化为0

vector<vector<int>> dp(n, vector<int>(4, 0));
dp[0][0] -= prices[0]; // 持股票

4.确定遍历顺序

从递归公式上可以看出，dp[i] 依赖于 dp[i-1]，所以是 从前向后 遍历

5.举例推导dp数组

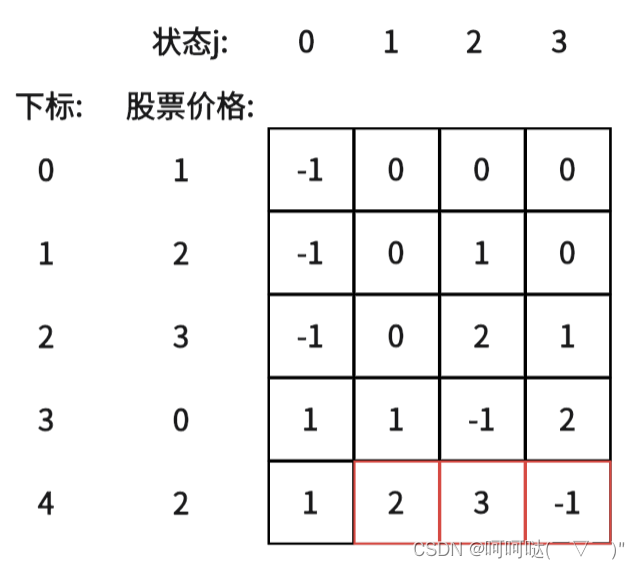
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        if (n == 0) return 0;
        vector<vector<int>> dp(n, vector<int>(4, 0));
        dp[0][0] -= prices[0]; // 持股票
        for (int i = 1; i < n; i++) {
            dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]));
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
            dp[i][2] = dp[i - 1][0] + prices[i];
            dp[i][3] = dp[i - 1][2];
        }
        return max(dp[n - 1][3], max(dp[n - 1][1], dp[n - 1][2]));
    }
};

时间复杂度：O(n)
空间复杂度：O(n)

其实，空间复杂度可以优化，定义一个dp[2][4]大小的数组就可以了，就保存前一天的当前的状态

>>优化空间复杂度

class Solution {
public:
    // 动态规划 滚动数组来节省空间
    int maxProfit(vector<int>& prices) {
        int len = prices.size();
        vector<vector<int>> dp(2,vector<int>(4,0));
        dp[0][0] = -prices[0];
        for(int i=1;i<len;i++) {
            dp[i % 2][0] = max(dp[(i-1) % 2][0],max(dp[(i-1) % 2][1] - prices[i],dp[(i-1) % 2][3] - prices[i]));
            dp[i % 2][1] = max(dp[(i-1) % 2][1],dp[(i-1) % 2][3]);
            dp[i % 2][2] = dp[(i-1) % 2][0] + prices[i];
            dp[i % 2][3] = dp[(i-1) % 2][2];
        }
        return max(dp[(len-1) % 2][1],max(dp[(len-1) % 2][2],dp[(len-1) % 2][3]));
    }
};