MNIST手写数字识别

news2025/1/11 0:43:25

MNIST是一个手写体数字的图片数据集，该数据集由美国国家标准与技术研究所（National Institute of Standards and Technology (NIST)）发起整理，其包含 60,000 张训练图像和 10,000 张测试图像，每张图片的尺寸为 28 x 28
在这里插入图片描述

线性回归

我们尝试通过线性回归模型识别手写数字，输入的图片是 28 x 28像素，我们可以将其看为 784 个变量，即：
$y = a_1x_1+a_2x_2+...+a_nx_n$

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf


# 计算梯度，并更新 [a1,a2,...,an],b 值
def gradient(a, b, x_array, y_array, learning_rate):
    a_gradient = tf.zeros([784, 1])
    b_gradient = 0
    length = len(x_array)
    # 计算梯度
    for i in range(0, length):
        x = x_array[i]
        y = y_array[i]
        base_gradient = (2 / length) * (np.dot(x, a) + b - y)[0]
        # print("base_gradient", base_gradient)
        a_gradient += base_gradient * tf.reshape(x, [784, 1])
        b_gradient += base_gradient

    # 更新 a、b 值
    new_a = a - learning_rate * a_gradient
    new_b = b - learning_rate * b_gradient
    return [new_a, new_b]


# 计算损失
def computer_loss(a, b, x_array, y_array):
    length = len(x_array)
    loss = 0
    # 计算梯度
    for i in range(0, length):
        x = x_array[i]
        y = y_array[i]
        loss += (np.dot(x, a) + b - y) ** 2
    loss /= length
    return loss


# 计算准确率
def computer_accuracy(a, b, x_array, y_array):
    accuracy = 0
    length = len(x_array)
    for i in range(0, length):
        x = x_array[i]
        y = np.dot(x, a) + b
        y = round(y[0])
        if y == y_array[i]:
            accuracy += 1
    return accuracy / length


mnist = tf.keras.datasets.mnist
(train_data, train_label), (test_data, test_label) = mnist.load_data()
train_size = len(train_data)
test_size = len(test_data)

# 手写数字图片是 28x28 的 Tensor，需要将其转换为 1x784
train_data_reshape = tf.reshape(train_data, [train_size, 784])
# 将 int 转换为 float，否则会有计算问题
train_data_reshape = tf.cast(train_data_reshape, dtype=tf.dtypes.float32)
print("train_data_reshape shape", np.shape(train_data_reshape))
# 对数据进行归一化处理
train_data_reshape = train_data_reshape / tf.constant(255.0, shape=[train_size, 784])
print("train_data_reshape", train_data_reshape)

test_data_reshape = tf.reshape(test_data, [test_size, 784])
test_data_reshape = tf.cast(test_data_reshape, dtype=tf.dtypes.float32)
train_data_reshape = test_data_reshape / tf.constant(255.0, shape=[test_size, 784])

# 假设 y = a1x1 + a2x2 +...+ anxn +b 且 x shape [1,784]，则 a shape 为 [784,1]
a = tf.random.normal([784, 1])
b = 0
loss_list = list()
accuracy_list = list()
for i in range(0, 1000):
    [a, b] = gradient(a, b, train_data_reshape, train_label, 0.01)
    if i % 10 == 0:
        loss = computer_loss(a, b, train_data_reshape, train_label)
        accuracy = computer_accuracy(a, b, test_data_reshape, test_label)
        print("loss = {} accuracy = {}".format(loss, accuracy))
        loss_list.append(loss)
        accuracy_list.append(accuracy)

print("a = {} b = {}".format(a, b))
l1 = plt.plot(loss_list, label="loss")
l2 = plt.plot(accuracy_list, label="accuracy")
plt.legend()
plt.show()

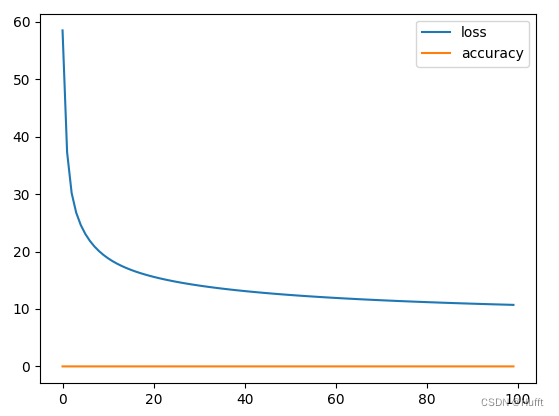
在这里插入图片描述
可以看出损失收敛在10左右，准确率只有15%左右，这是因为该模型存在两个问题：

如果预测的数据是 2.5，那实际值应该是2还是3呢？所以应该通过概率来解决该问题，它需要输出多个结果，例如：1的概率为0.999，2的概率为0.0001，3的概率为0.0001等，最终所有结果的概率综合为1。我们称这样的问题为分类问题。
图片像素与数字并非线性关系，而是复杂的非线性关系

非线性分类

多输出问题

对于多个结果我们可以考虑使用矩阵的形式，例如 1x4 阶矩阵，需要输出 2 个结果，则可以进行如下运算：
${\begin{bmatrix} a&b&c&d\\ \end{bmatrix}} * {\begin{bmatrix} 1&5\\ 2&6\\ 3&7\\ 4&8\\ \end{bmatrix}} = {\begin{bmatrix} 1a+2b+3c+4d&5a+6b+7c+8d\\ \end{bmatrix}}$
手写数字需要10个结果，即 [10] 矩阵，每列的值代表数字 n 的概率，例如表示1的概率为0.999：
${\begin{bmatrix} 0.999 & 0.0001 & 0.0001& 0.0001& 0.0001& 0.0001& 0.0001& 0.0001& 0.0001& 0.0001 \end{bmatrix}}$
因为 $x$ 为 $[n, 784]$ 矩阵，所以应该给 $x$ 点乘一个 $[784, 10]$ 矩阵，由此多个输出问题得以解决。

非线性问题

我们需要针对线性模型中增加非线性因子，使其变为非线性，这里采用ReLU函数：
在这里插入图片描述
即 $y = re l u (a x + b)$ ，其中 $a = [784, 10]$ ， $y = [10]$

# 线性回归模型识别手写数字

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf

np.set_printoptions(edgeitems=10, linewidth=200)

mnist = tf.keras.datasets.mnist
(train_data, train_label), (test_data, test_label) = mnist.load_data()
train_size = len(train_data)
test_size = len(test_data)

# 将 numpy.ndarray 类型数据转换为 Tensor
train_data = tf.convert_to_tensor(train_data, dtype=tf.dtypes.float32)
# 手写数字图片是 28x28 的 Tensor，需要将其转换为 1x784
train_data = tf.reshape(train_data, [train_size, 784])
# 对数据进行归一化处理
train_data = train_data / 255.
print("train_data", train_data)

# 对 label 进行 one_hot 编码
train_label = tf.convert_to_tensor(train_label, dtype=tf.dtypes.int8)
train_label = tf.one_hot(train_label, 10)

# 沿着第一个维度切片，将 train_data、train_label 转换为 tf.data.Dataset 对象，并按60个合为一个数据集
train_batch = tf.data.Dataset.from_tensor_slices((train_data, train_label)).batch(60)
print("train_batch", train_batch)

# 准备测试集数据
test_data = tf.convert_to_tensor(test_data, dtype=tf.dtypes.float32)
test_data = tf.reshape(test_data, [test_size, 784])
test_data = test_data / 255
test_label = tf.one_hot(test_label, 10)

model = tf.keras.Sequential([
    tf.keras.layers.Dense(10, activation='relu')
])
optimizer = tf.optimizers.SGD(learning_rate=0.01)


def computer_acc():
    # 预测测试集结果
    test_out = model.predict(test_data)
    # 将概率最大置1，其他置0
    max_val = tf.reduce_max(test_out, axis=1)
    max_val = tf.reshape(max_val, [-1, 1])
    test_out = tf.where(tf.equal(test_out, max_val), tf.ones_like(test_out), tf.zeros_like(test_out))
    # 降维，判断整行数据是否相等
    acc = tf.reduce_all(tf.equal(test_out, test_label), axis=1)
    return tf.reduce_mean(tf.cast(acc, tf.float32))


loss_list = list()
acc_list = list()
for i in range(0, 1000):
    for (x, y) in train_batch:
        # -1 表示自动推断
        x = tf.reshape(x, (-1, 784))
        with tf.GradientTape() as tape:
            out = model(x)
            loss = tf.reduce_sum(tf.square(out - y) / x.shape[0])
        # 计算梯度
        gradient = tape.gradient(loss, model.trainable_variables)
        # 反向传递
        optimizer.apply_gradients(zip(gradient, model.trainable_variables))
    if i % 10 == 0:
        loss_list.append(loss)
        acc = computer_acc()
        acc_list.append(acc)
        print("i = {} loss = {} acc = {}".format(i, loss, acc))

l1 = plt.plot(loss_list, label="loss")
l2 = plt.plot(acc_list, label="acc")
plt.legend()
plt.show()

在这里插入图片描述
最终准确率收敛在了 84% 左右，原因是增加一个非线性因素可能不够，所以我们需要增加多个，使其可以拟合更复杂的非线性函数：
$out_1 = relu(a_1 x + b)$ ，其中 $a_1 = [784,512]$ ， $out_1 = [512]$
$out_2 = relu(a_2 out_1 + b)$ ，其中 $a_1 = [512,256]$ ， $out_1 = [256]$
$out_3 = relu(a_3 out_2 + b)$ ，其中 $a_1 = [256,10]$ ， $out_3 = [10]$

model = tf.keras.Sequential([
    tf.keras.layers.Dense(512, activation='relu'),
    tf.keras.layers.Dense(256, activation='relu'),
    tf.keras.layers.Dense(10)
])