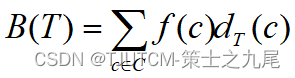235. 二叉搜索树的最近公共祖先
具体思路就是当小于pq的时候就往右取遍历,当大于的时候就往左遍历;
lass Solution {
public:
TreeNode* traversal(TreeNode* current, TreeNode* p, TreeNode* q) {
if (current->val > p->val && current->val > q->val) { //如果根节点大于pq,就往左子树找
TreeNode* left = traversal(current->left, p, q); //如果左子树找到了的话就定义一个treenode类型的变量把这个数值接住
//if (left != NULL) { //由于题目写了肯定找得到,所以这个判断语句不写也能过
return left;
// }//如果没找到left就是空的
}
if (current->val < p->val && current->val < q->val) { //如果根节点大于pq,就往左子树找
TreeNode* right = traversal(current->right, p, q); //如果左子树找到了的话就定义一个treenode类型的变量把这个数值接住
//if (right != NULL) {
return right;
// }//如果没找到那right就是空的
}
return current;//这就是第三中情况,不走前面两种if的时候就是找到了直接输出;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
TreeNode *result = new TreeNode(0);
result = traversal(root, p, q);
return result;
}
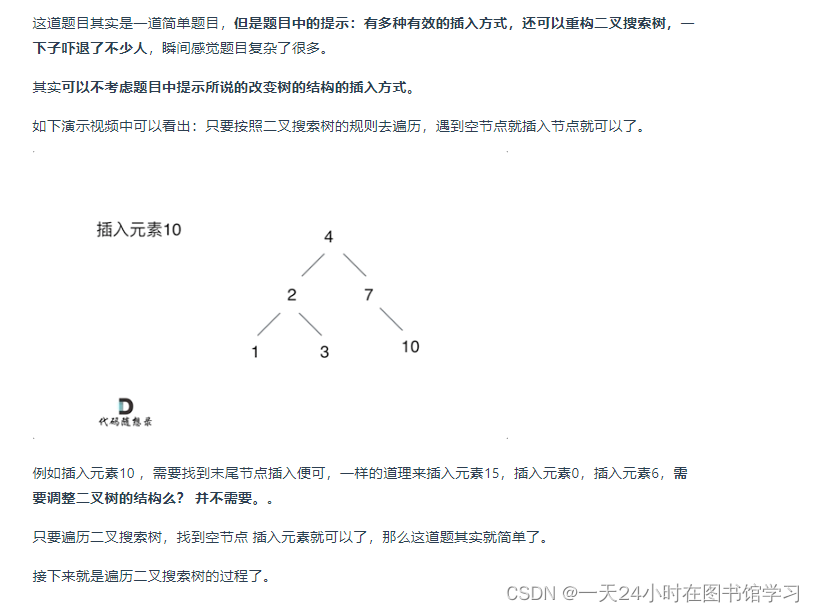
};701.二叉搜索树中的插入操作
简单题自己可以写出来,这个题递归函数需要返回值不然还需要记录下前一个节点的位置,然后再让前一个节点指向后一个节点
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
//TreeNode* extra_node = new TreeNode(val);
if (root == NULL) {
TreeNode* extra_node = new TreeNode(val);
root = extra_node;
return root;
}
if (root->val > val) {
root->left = insertIntoBST(root->left, val);
}
if (root->val < val) {
root->right = insertIntoBST(root->right, val);
}
return root;
}
};450.删除二叉搜索树中的节点
总体结构还是比较简单的,就是五种分类方法有点麻烦
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if (root == nullptr) return root; // 第一种情况:没找到删除的节点,遍历到空节点直接返回了
if (root->val == key) {
// 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
if (root->left == nullptr && root->right == nullptr) {
///! 内存释放
delete root;
return nullptr;
}
// 第三种情况:其左孩子为空,右孩子不为空,删除节点,右孩子补位 ,返回右孩子为根节点
else if (root->left == nullptr) {
TreeNode* retNode = root->right;
///! 内存释放
delete root;
return retNode;
}
// 第四种情况:其右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
else if (root->right == nullptr) {
TreeNode* retNode = root->left;
///! 内存释放
delete root;
return retNode;
}
// 第五种情况:左右孩子节点都不为空,则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置
// 并返回删除节点右孩子为新的根节点。
else {
TreeNode* cur = root->right; // 找右子树最左面的节点
while(cur->left != nullptr) {
cur = cur->left;
}
cur->left = root->left; // 把要删除的节点(root)左子树放在cur的左孩子的位置
TreeNode* tmp = root; // 把root节点保存一下,下面来删除
root = root->right; // 返回旧root的右孩子作为新root
delete tmp; // 释放节点内存(这里不写也可以,但C++最好手动释放一下吧)
return root;
}
}
if (root->val > key) root->left = deleteNode(root->left, key);
if (root->val < key) root->right = deleteNode(root->right, key);
return root;
}
};