1.Scan details

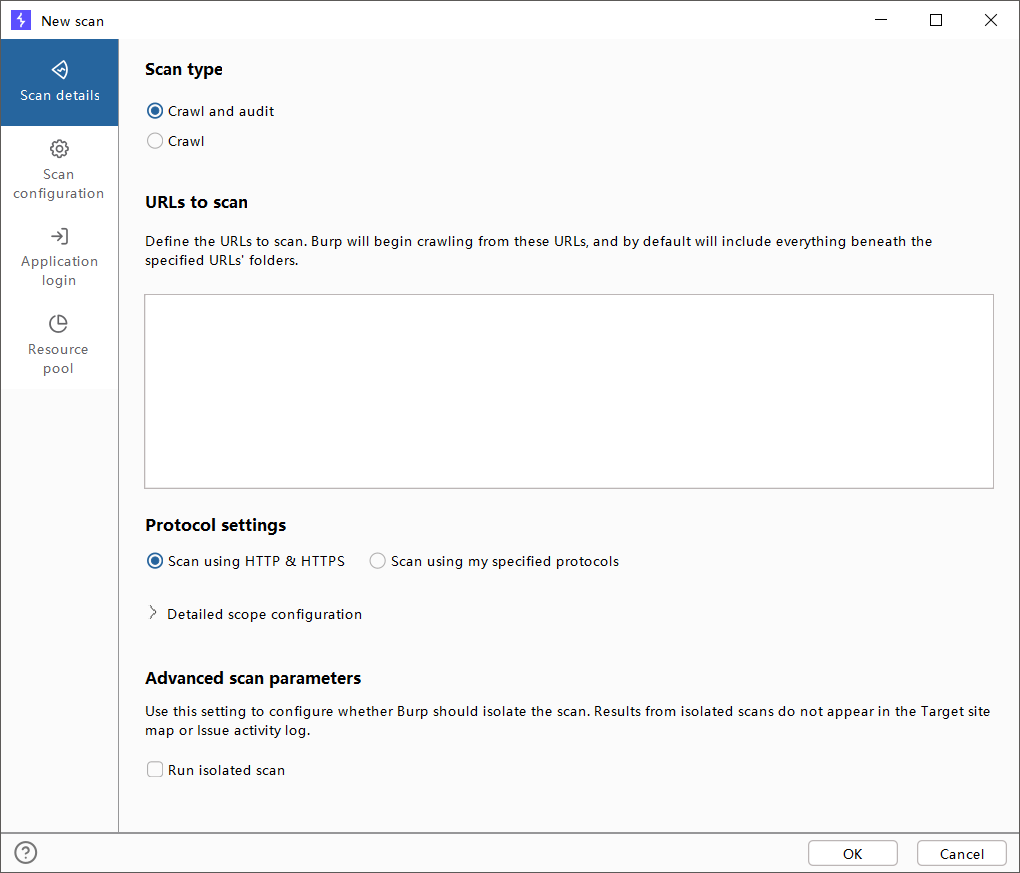
解释：选择只是爬行还是爬行加代码审计

• Scan Type：选择爬行或者代码审计
• URLs to scan：定义要扫描的网址。Burp将从这些网址开始进行爬行，并默认将包括指定网址文件夹下的所有内容。
• Protocol settings：使用URL前缀或高级匹配规则来配置更详细的范围配置。注意，待扫描的URL必须位于定义的范围内，并且仍将用作爬行的起始点。
• Advanced scan parameters：使用此设置来配置Burp是否应该隔离扫描。隔离扫描的结果不会显示在目标站点地图或问题活动日志中。

2.Scan configuration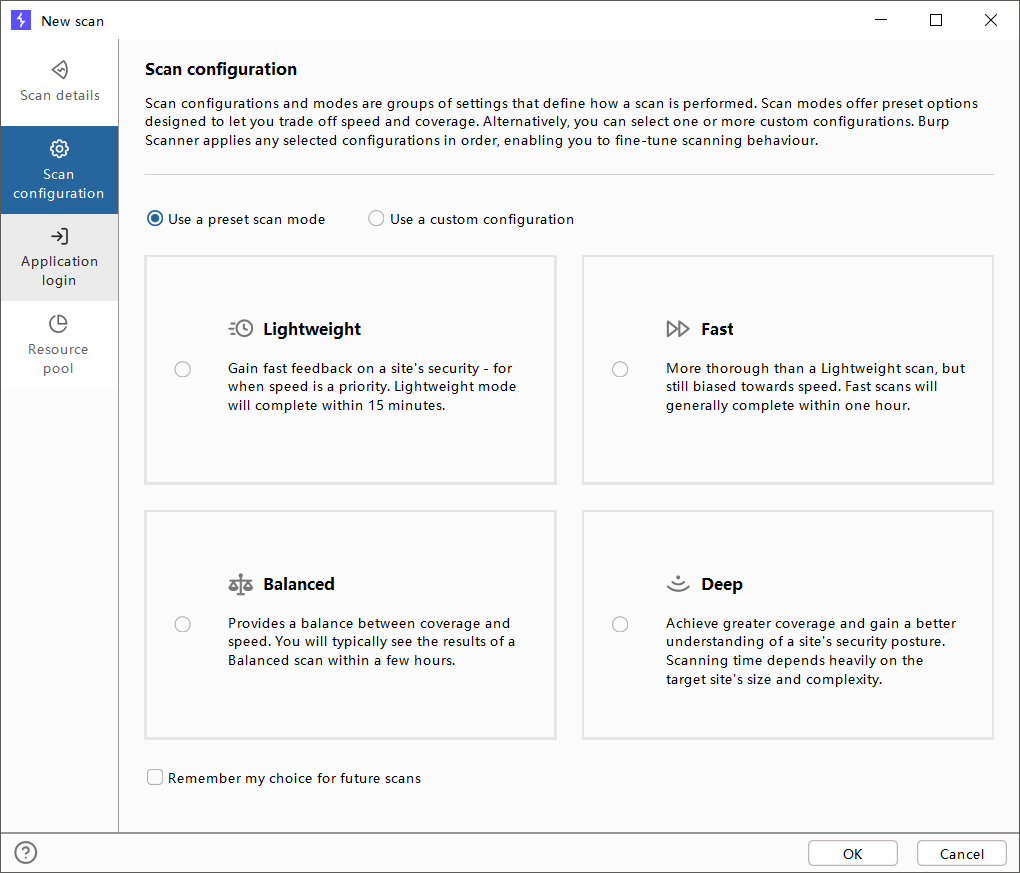

解释：扫描的配置（扫描配置和模式是一组设置，用于定义扫描的执行方式。扫描模式提供了预设选项，旨在让您在速度和覆盖范围之间进行权衡。或者，您可以选择一个或多个自定义配置。BurpScanner按顺序应用所选的配置，使您能够调整扫描行为。）（可使用自定义配置）

实操：

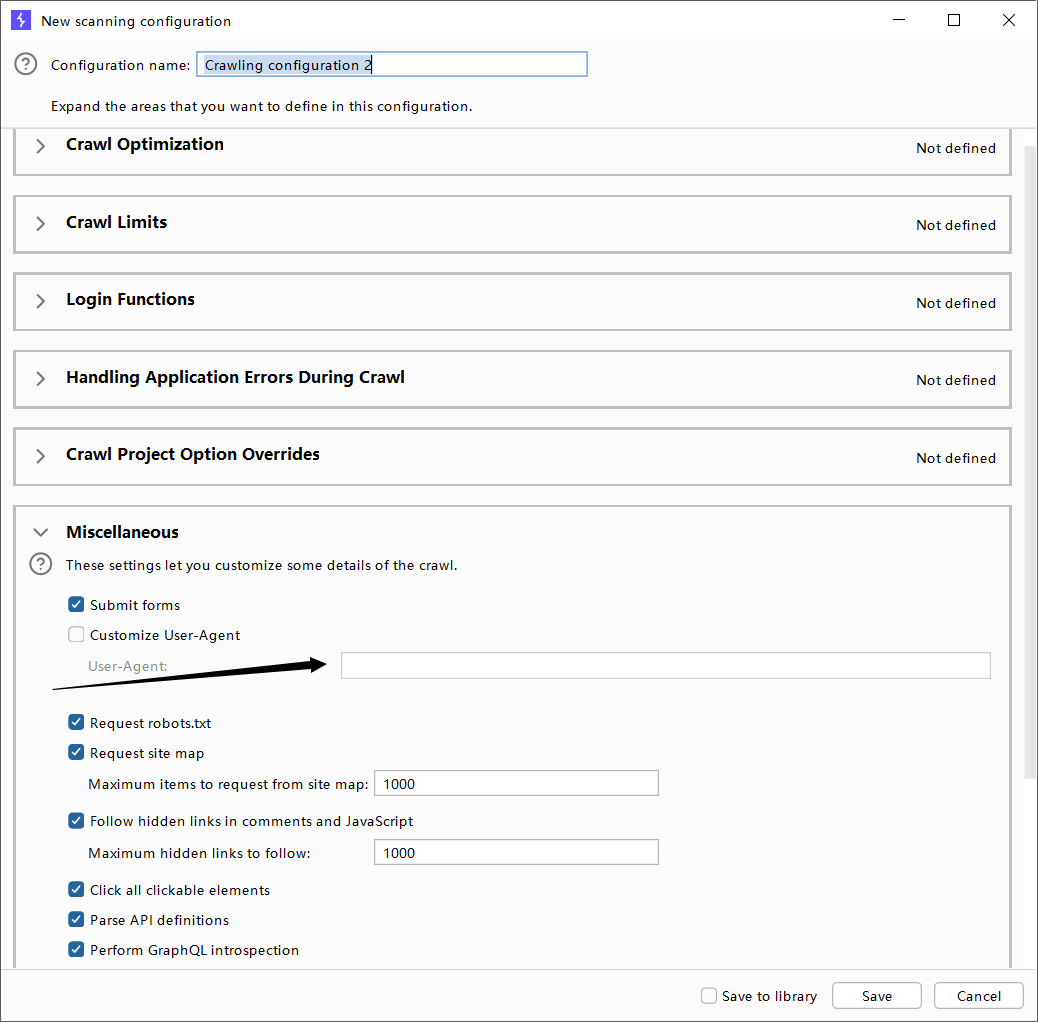
• 修改访问时的User-Agent：先选择自定义配置，然后点击new，然后点击
  

3.Application login

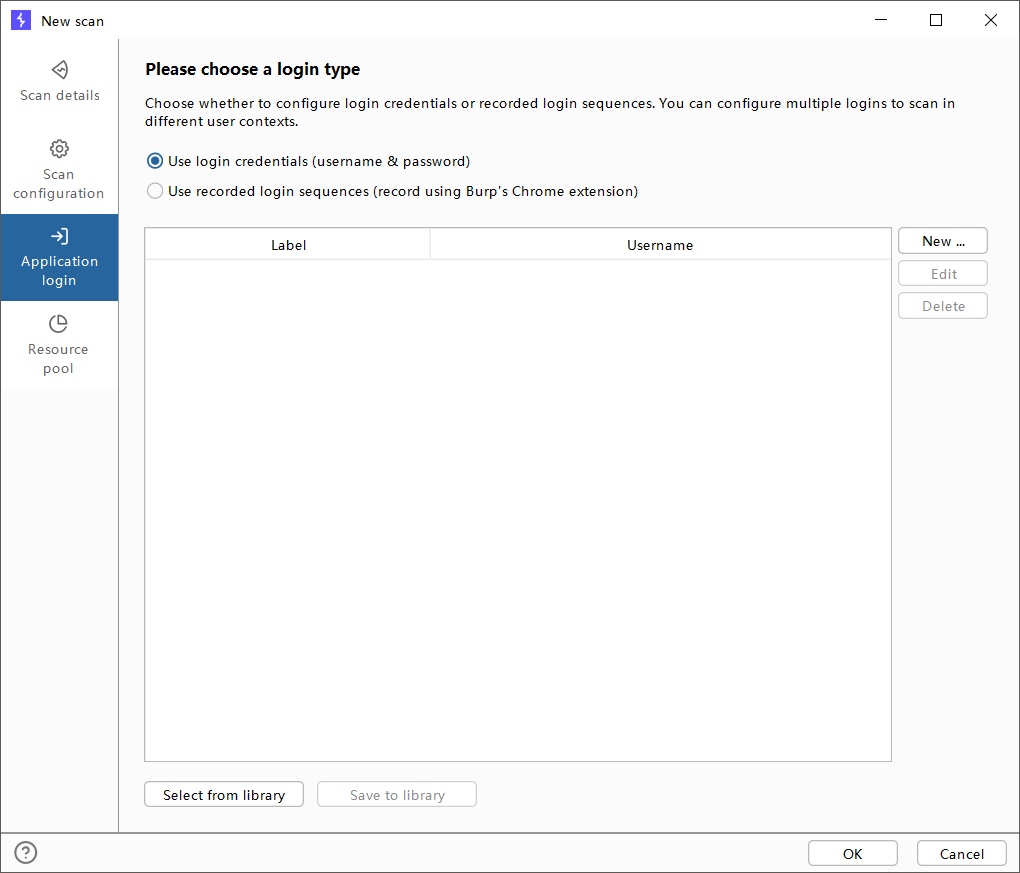
解释：设置扫描时候的登录选项

实操：

• 设置可能遇到登录时，输入的账号密码
  

4.Resource pool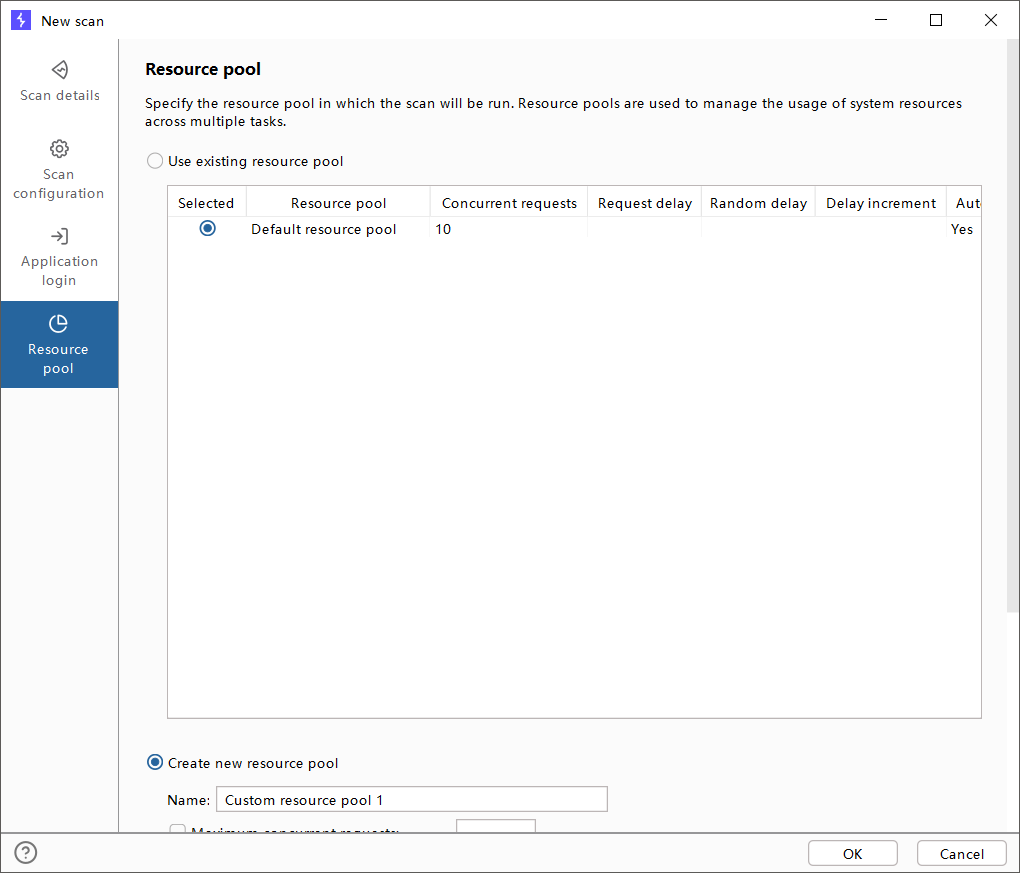

解释：设置访问时的资源池（通常来配置访问速率等等）