目录
- 欧拉函数
- 一、用公式求
- 代码
- 二、线性筛法求欧拉函数
- 扩展欧拉定理
欧拉函数
AcWing 873. 欧拉函数
一、用公式求
- 定义:1 ~ N 中与 N 互质的数的个数被称为欧拉函数,记为ϕ(N)。
怎么求呢??
有一个公式:
N = p1a1 X p2a2 X p3a3……X pkak ;
ϕ(N) = N(1 - 1/p1) X N(1 - 1/p2) X N(1 - 1/p3) ……X N(1 - 1/pk);- 例子:
N= 6 = 2 X 3;
ϕ(N) = 6 X (1 - 1/2)X (1 - 1/3) = 2- 证明:容斥原理 。
1 ~ n 中n的质因子有 p1a1 X p2a2 X p3a3……X pkak ;
1.从1~ n中去掉 p1a1、 p2a2 、 p3a3……、 pkak 的倍数。
=>N - N / p1 - N / p2 - N / p3 …… N / pk
2.把所有重复减去的倍数加上。=> + N/(pi X pj…)
3.减去所有pipj…pk的倍数……
……
4.以此类推,得到ϕ(N) = N(1 - 1/p1) X N(1 - 1/p2) X N(1 - 1/p3) ……X N(1 - 1/pk);
代码
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin >> n;
while(n --){
int a;
cin >> a;
int res = a;
for(int i = 2; i <= a / i; i ++)
if(a % i == 0){
res = res / i * (i - 1);
while (a % i == 0) a /= i;
}
if(a > 1)
res = res / a * (a - 1);
cout << res << endl;
}
return 0;
}
二、线性筛法求欧拉函数
AcWing 874. 筛法求欧拉函数
O(n) : 线性筛法模板,可以求出来很多东西。
线性筛法模板:
ll get_eulers(int n){
for(int i = 2; i <= n;i ++){
if(!st[i])//如果没被筛去,说明是质数
primes[cnt ++] = i;//将质数入队
for(int j = 0 ; primes[j] <= n / i;j ++){//干掉i的倍数
st[primes[j] * i] = 1;
if(i % primes[j] == 0)
break;
}
}
}
再进行更改:
ll get_eulers(int n){
phi[1] = 1;//1当中与1互质的只有1自己
for(int i = 2; i <= n;i ++){
if(!st[i]){
primes[cnt ++] = i;
phi[i] = i - 1;//如果一个数i是质数,那么它的欧拉函数值应该是 i-1
}
for(int j = 0 ; primes[j] <= n / i;j ++){
st[primes[j] * i] = 1;
if(i % primes[j] == 0){
phi[primes[j] * i] = phi[i] * primes[j];
/*
i % primes[j] == 0时, primes[j]是i的一个质因子
phi[i * primes[j]]只是比phi[i]多了一个primes[j]而已,
primes[j]是i的一个质因子,所以
phi[i]里面已经有一个(1-1/pj)了,
所以phi[primes[j] * i]是i的欧拉值乘上i的质因子primes[j]
*/
break;
}
phi[primes[j] * i] = phi[i] * (primes[j] - 1);
/*
如果i % primes[j] != 0时, primes[j]是i的非质因子
那么 phi[primes[j] * i] = primes[j] * phi[i] * (1-(primes[j] - 1) / primes[j])
即 phi[primes[j] * i] = phi[i] * (primes[j] - 1);
*//
}
}
}
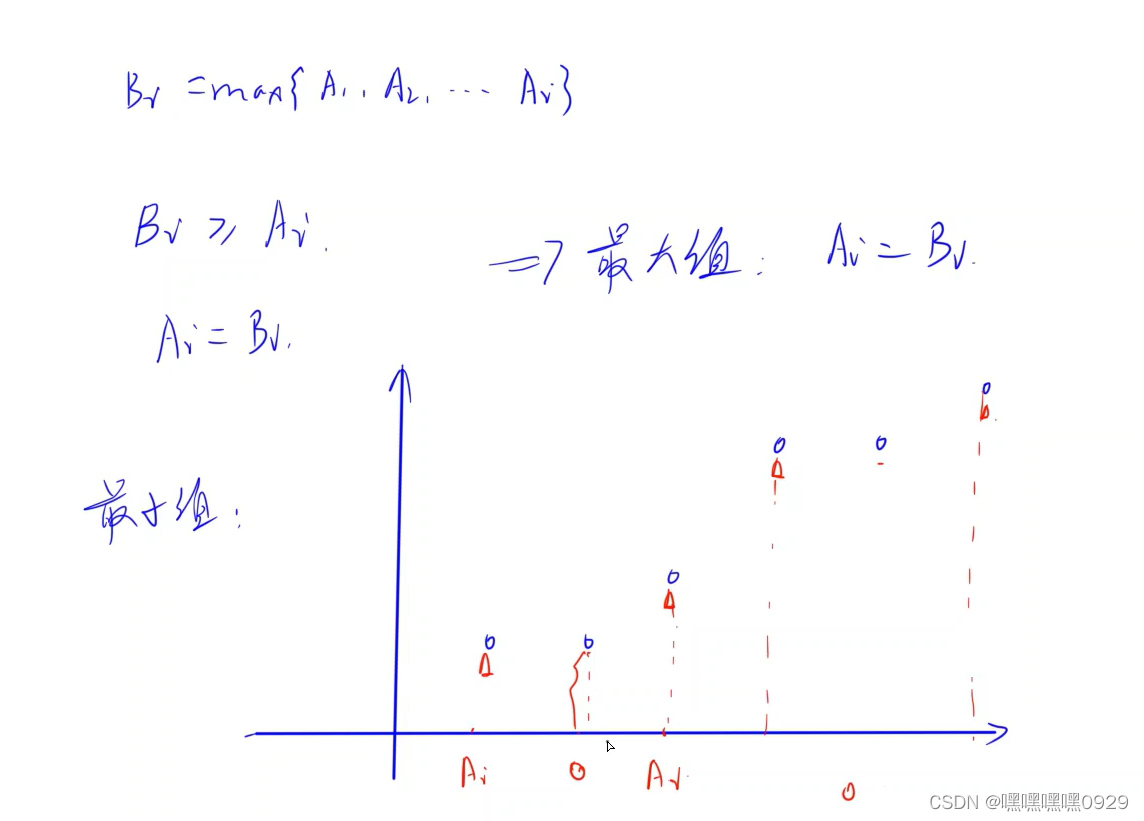
扩展欧拉定理


2021-08-26









![[题]修剪草坪 #单调队列优化](https://img-blog.csdnimg.cn/20210201211628892.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NTkxNjk1OQ==,size_16,color_FFFFFF,t_70)