---

一、曲线积分

1.2 对坐标的曲线积分（第二类曲线积分）

1.2.1 问题产生 —— 做功问题

（1）如下图所示，在大小和方向都不变的力 $\overrightarrow{F}$ 的作用下物体沿水平方向从 A 点移动到 B 点，力对物体做功为 $W=|\overrightarrow{F}|\cos \theta \cdot |\overrightarrow{AB}|=\overrightarrow{F}\cdot \overrightarrow{AB}$ ，其中 $\theta$ 为 $\overrightarrow{F},\overrightarrow{AB}$ 的夹角。

（2）二维空间物体在变力作用下沿有向曲线段运动，力对物体做功。设 F → ( x , y ) = { P ( x , y ) , Q ( x , y ) } \overrightarrow{F}(x,y)=\{P(x,y),Q(x,y)\} F (x,y)={P(x,y),Q(x,y)} ，即水平方向的力为 $P$ ，竖直方向的力为 $Q$ 。$L$ 为 $xOy$ 平面内的有向曲线段，物体在力 $\overrightarrow{F}(x,y)$ 的作用下沿着 $L$ 从起点 A 到终点 B（下图），可以利用元素法的思想，求力所做的功。

取 d s → ⊂ L , d s → = { d x , d y } d\overrightarrow{s}\sub L,d\overrightarrow{s}=\{dx,dy\} ds ⊂L,ds ={dx,dy} ，则有 $dW=\overrightarrow{F}(x,y)\cdot d\overrightarrow{s}=P(x,y)dx+Q(x,y)dy$ ，于是 $$W={\int }_{L}P(x,y)dx+Q(x,y)dy.$$

1.2.2 对坐标的曲线积分的定义（了解）

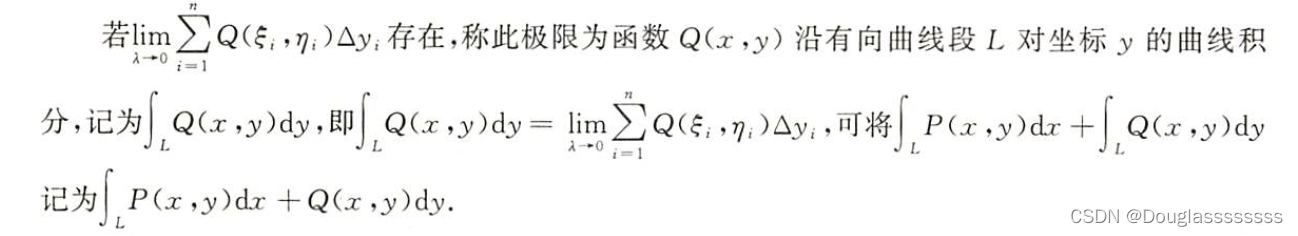
1.2.3 对坐标的曲线积分的性质

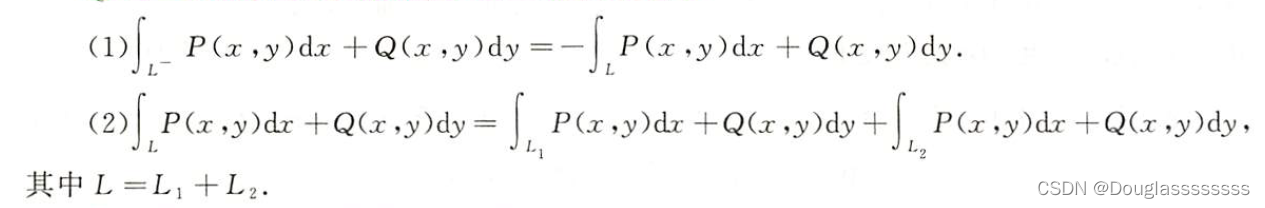
1.2.4 二维空间对坐标的曲线积分计算法

1. 定积分法

（1）设有向曲线段 $L:y=\phi (x)$ ，$L$ 的起点对应为 $x=a$ ，终点对应为 $x=b$ ，则 ∫ L P ( x , y ) d x + Q ( x , y ) d y = ∫ a b { P [ x , φ ( x ) ] + Q [ x , φ ( x ) ] φ ′ ( x ) } d x . \int_LP(x,y)dx+Q(x,y)dy=\int_a^b\{P[x,\varphi(x)]+Q[x,\varphi(x)]\varphi'(x)\}dx. ∫L​P(x,y)dx+Q(x,y)dy=∫ab​{P[x,φ(x)]+Q[x,φ(x)]φ′(x)}dx. （2）设有向线段 $$L:\{\begin{array}{l}x=\phi (t),\\ y=u(t),\end{array}(\alpha \le t\le \beta )$$ 则 ∫ L P ( x , y ) d x + Q ( x , y ) d y = ∫ α β { P [ φ ( t ) , u ( t ) ] φ ′ ( t ) + Q [ φ ( t ) , u ( t ) ] u ′ ( t ) } d t 则\int_LP(x,y)dx+Q(x,y)dy=\int_\alpha^\beta\{P[\varphi(t),u(t)]\varphi'(t)+Q[\varphi(t),u(t)]u'(t)\}dt 则∫L​P(x,y)dx+Q(x,y)dy=∫αβ​{P[φ(t),u(t)]φ′(t)+Q[φ(t),u(t)]u′(t)}dt 【例】求以下情况下的曲线积分 ${\int }_L(2y+1)dx+(2x-3)dy:$

（1）$L$ 是经点 $O(0,0)$ 经 $y=x$ 到点 $A(1,1)$ 的有向曲线段；

（2）$L$ 是经点 $O(0,0)$ 经 $y=x^2$ 到点 $A(1,1)$ 的有向曲线段；

解： （1）${\int }_L(2y+1)dx+(2x-3)dy={\int }_0^1(2x+1+2x-3)dx={\int }_0^1(4x-2)dx=0.$

（2）${\int }_L(2y+1)dx+(2x-3)dy={\int }_0^1[(2x^2+1+(2x-3)\cdot 2x]dx=0.$

2. 二重积分法（格林公式）

定理 1 —— 设 $D$ 为 $xOy$ 平面上连通的有限闭区域，$L$ 为闭区域 $D$ 上的正向边界曲线，函数 $P(x,y),Q(x,y)$ 在 $D$ 上连续可偏导，则 $${\oint }_{L}P(x,y)dx+Q(x,y)dy={\iint }_D(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy.$$ 若 $L$ 为负向边界，则结果为相反数；若 $L$ 不封闭，可以补充曲线段再使用格林公式；若函数 $P(x,y),Q(x,y)$ 有不连续可偏导的点，一般可以将区域 $D$ 划为若干区域，再使用格林公式。

3. 曲线积分与路径无关的条件

定理 2 —— 设 $D$ 为单连通区域，函数 $P(x,y),Q(x,y)$ 在区域 $D$ 内连续可偏导，则下列四个命题等价。

1. 曲线积分 ${\int }_{L}P(x,y)dx+Q(x,y)dy$ 与路径无关。
2. 对区域 $D$ 内任意闭曲线 $C$ ，有 ${\oint }_{C}P(x,y)dx+Q(x,y)dy=0$ 。
3. 区域内恒有 $\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y}$（柯西 — 黎曼条件）。
4. 在区域内存在二元函数 $u(x,y)$ ，使得 $du(x,y)=P(x,y)dx+Q(x,y)dy.$

（1）若 $\frac{\partial Q}{\partial x}\equiv \frac{\partial P}{\partial y}$ ，则沿从点 $(x_0,y_0)$ 到点 $(x_1,y_1)$ 的有向曲线段 $L$ 的曲线积分可表示为 $${\int }_{L}P(x,y)dx+Q(x,y)dy={\int }_{(x_0,y_0)}^{(x_1,y_1)}P(x,y)dx+Q(x,y)dy$$$$={\int }_{x_0}^{x_1}P(x,y_0)dx+{\int }_{y_0}^{y_1}Q(x_1,y)dy.$$ （2）若 $\frac{\partial Q}{\partial x}\equiv \frac{\partial P}{\partial y}$ ，且存在 $u(x,y)$ ，使得 $du(x,y)=P(x,y)dx+Q(x,y)dy$ ，则$${\int }_{L}P(x,y)dx+Q(x,y)dy={\int }_{(x_0,y_0)}^{(x_1,y_1)}P(x,y)dx+Q(x,y)dy$$$$=u(x,y){|}_{(x_0,y_0)}^{(x_1,y_1)}=u(x_1,y_1)-u(x_0,y_0).$$ （3）若 $\frac{\partial Q}{\partial x}\equiv \frac{\partial P}{\partial y}$ ，则 $$u(x,y)={\int }_{(x_0,y_0)}^{(x,y)}P(x,y)dx+Q(x,y)dy={\int }_{x_0}^{x}P(x,y_0)dx+{\int }_{y_0}^{y}Q(x,y)dy.$$ （4）对微分方程 $P(x,y)dx+Q(x,y)dy=0$ ，若 $\frac{\partial Q}{\partial x}\equiv \frac{\partial P}{\partial y}$ ，则称该方程为全微分方程。令 $$u(x,y)={\int }_{(x_0,y_0)}^{(x,y)}P(x,y)dx+Q(x,y)dy$$ 有 $du(x,y)=P(x,y)dx+Q(x,y)dy$ ，则有原方程的通解为 $u(x,y)=C.$

【例】求解方程 $(x{y}^2+y)dx+(x^{2}y+x-2y)dy=0$ ，令 $P(x,y)=x{y}^2+y,Q(x,y)=x^{2}y+x-2y$ ，有 $\partial Q/\partial x=2xy+1=\partial P/\partial y$ ，故其为一个全微分方程。

对原方程进行整理有： $x{y}^{2}dx+x^{2}ydy+ydx+xdy-2ydy=d(\frac{1}{2}{x}^2{y}^2+xy-y^2)=0$ ，故原方程通解为 $\frac{1}{2}{x}^2{y}^2+xy-y^2=C.$

4. 两类曲线积分之间的关系

$${\int }_{L}P(x,y)dx+Q(x,y)dy={\int }_L[P(x,y)\cos \alpha +Q(x,y)\cos \beta ]ds,$$ 其中，$\cos \alpha ,\cos \beta$ 为曲线 $L$ 上点 $(x,y)$ 上的切向量的方向余弦。

1.2.5 三维空间对坐标的曲线积分的计算

1. 定积分法

设
$$L:\{\begin{array}{l}x=\phi (t),\\ y=u(t),\\ z=w(t),\end{array}(\alpha \le t\le \beta )$$$$则{\int }_{L}P(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz$$ = ∫ α β { P [ φ ( t ) , u ( t ) , w ( t ) ] φ ′ ( t ) + Q [ φ ( t ) , u ( t ) , w ( t ) ] u ′ ( t ) + R [ φ ( t ) , u ( t ) , w ( t ) ] w ′ ( t ) } d t . =\int_\alpha^\beta\{P[\varphi(t),u(t),w(t)]\varphi'(t)+Q[\varphi(t),u(t),w(t)]u'(t)+R[\varphi(t),u(t),w(t)]w'(t)\}dt. =∫αβ​{P[φ(t),u(t),w(t)]φ′(t)+Q[φ(t),u(t),w(t)]u′(t)+R[φ(t),u(t),w(t)]w′(t)}dt.

2. 斯托克斯公式（Stokes）

---

写在最后

好难啊，三维的先放一放吧，二维的直观上也不好理解，多花些时间练习下吧。

曲线积分的内容就到此结束了，把这些消化好，我们再继续学习曲面积分！