系列文章
【管理运筹学】第 5 章 | 整数规划 (1,问题提出与分支定界法)
【管理运筹学】第 5 章 | 整数规划 (2,割平面法及 0-1 变量的特性)
【管理运筹学】第 5 章 | 整数规划 (3,隐枚举法计算步骤)
【管理运筹学】第 5 章 | 整数规划(4,指派问题)
文章目录
- 系列文章
- 引言
- 五、指派问题
- 5.1 指派问题的数学模型
- 5.2 匈牙利算法
- 5.3 非标准的指派问题
- 写在最后
引言
都忘了当初为什么跳过指派问题,直接学运输问题了,可能是发现指派问题有些内容需要运输问题作为铺垫吧。
五、指派问题
5.1 指派问题的数学模型
在生活中,常常遇到这样的问题:某单位需要完成 n n n 项任务,恰好有 n n n 个人可以承担这些任务。由于每个人的专长不同,各人完成的任务不同,效率(或所需时间)也不同。应指派哪个人去完成哪项任务,能使得完成这 n n n 项任务的总效率最高(或所需总时间最少)。这类问题称为指派问题或分派问题(assignment problem)。
【例 1】有一份中文说明书,需要翻译成英、日、德、俄 4 种文字,分别记作 E , J , G , R E,J,G,R E,J,G,R 。现有甲、乙、丙、丁 4 人,他们将中文翻译为各种语言所需时间如下表所示。问如何指派完成工作,使得总所需时间最少?
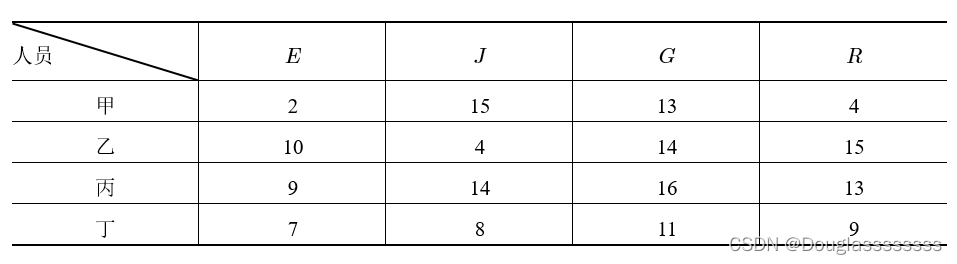
对于每个指派问题,都有类似上表的数表,称为效率矩阵或系数矩阵,其元素
c
i
j
>
0
c_{ij}>0
cij>0 ,表示第
i
i
i 人去完成第
j
j
j 项任务所需时间。解题时需引入 0-1 变量
x
i
j
x_{ij}
xij ,令
x
i
j
=
{
1
,
指派第
i
人去完成第
j
项工作时
0
,
不指派第
i
人去完成第
j
项工作时
x_{ij}=\begin{cases} 1,& 指派第 i 人去完成第j项工作时 \\ 0,&不指派第 i 人去完成第j项工作时 \end{cases}
xij={1,0,指派第i人去完成第j项工作时不指派第i人去完成第j项工作时 当是求最小化问题时,可建立如下数学模型:
min
z
=
∑
i
∑
j
c
i
j
x
i
j
(1)
\min{z}=\sum_i\sum_jc_{ij}x_{ij}\tag{1}
minz=i∑j∑cijxij(1)
s
.
t
.
{
∑
i
x
i
j
=
1
∑
j
x
i
j
=
1
x
i
j
=
0
或
1
s.t.\begin{cases} \sum_ix_{ij}=1\\ \sum_jx_{ij}=1 \\ x_{ij}=0 或 1\end{cases}
s.t.⎩
⎨
⎧∑ixij=1∑jxij=1xij=0或1 约束条件规定了一个人只能完成一项任务,一项任务只能交给一个人去做。
指派问题是 0-1 规划的一个特例,也是运输问题的一个特例,即当总产量是 1 ,总销量也是 1 的产销平衡运输问题。显然可以利用 0-1 规划的隐枚举法和运输问题的表上作业法去求解指派问题,不过同利用单纯形法求解运输问题一样不太合算,指派问题有专门的算法进行简便求解。
5.2 匈牙利算法
指派问题的最优解有这样的性质,若从系数矩阵( c i j c_{ij} cij)的一行(列)中分别减去该行(列)的最小元素,得到新矩阵( b i j b_{ij} bij)。以其作为系数矩阵求解指派问题得到的最优解和用原来的系数矩阵求解的最优解相同。
利用上述性质,原系数矩阵可以变换为含有许多零元素的新系数矩阵,同时保持最优解不变。在系数矩阵( b i j b_{ij} bij)中,我们关心位于不同行不同列的零元素,称其为独立零元素。
若能在系数矩阵( b i j b_{ij} bij)中找到 n n n 个独立的零元素,令解矩阵 ( x i j x_{ij} xij)中对应 n n n 个独立零元素的位置元素取值为 1 ,其余元素取值为 0 。将其代入 z b = ∑ ∑ b i j x i j z_b=\sum\sum b_{ij}x_{ij} zb=∑∑bijxij 中,得到 z b = 0 z_b=0 zb=0 ,此解即为指派问题的最优解。
库恩(W.W.Kuhn)于 1955 年提出了指派问题的解法,他引用了匈牙利数学家康尼格(D.Koning)一个关于矩阵中 0 元素的定理:系数矩阵中独立 0 元素的最多个数等于能覆盖所有 0 元素的最少直线数。下面利用 5.1 节中的翻译问题(例 1)来说明此算法的步骤。
Step 1: 对系数矩阵进行变换:1. 系数矩阵每行元素减去该行最小的元素;2. 接着将系数矩阵每列元素减去该列最小元素。若某行(列)中已有 0 元素,则不必处理。
例 1 中的系数矩阵为 ( c i j ) = [ 2 15 13 4 10 4 14 15 9 14 16 13 7 8 11 9 ] (c_{ij})=\begin{bmatrix} 2 & 15 & 13 & 4 \\ 10 & 4 & 14 & 15 \\ 9 & 14 & 16 & 13 \\ 7 & 8 & 11 & 9\end{bmatrix} (cij)= 2109715414813141611415139 ,每行减去该行最小零元素,可得 [ 0 13 11 2 6 0 10 11 0 5 7 4 0 1 4 2 ] \begin{bmatrix} 0 & 13 & 11 & 2 \\ 6 & 0 & 10 & 11 \\ 0 & 5 & 7 & 4 \\ 0 & 1 & 4 & 2\end{bmatrix} 06001305111107421142 ,接着每列减去该列最小元素,可得 ( b i j ) = [ 0 13 7 0 6 0 6 9 0 5 3 2 0 1 0 0 ] . (b_{ij})=\begin{bmatrix} 0 & 13 & 7 & 0 \\ 6 & 0 & 6 & 9 \\ 0 & 5 & 3 & 2 \\ 0 & 1 & 0 & 0\end{bmatrix}. (bij)= 06001305176300920 .
Step 2: 进行试指派,以寻求最优解。
经过第一步后,各行各列已经有了 0 元素,但有些并非独立的零元素(所在行或列唯一零元素)。当 n n n 较小时,可以直接观察、试探出 n n n 个独立的零元素;但当 n n n 较大时,需按照一定步骤进行搜寻,如下:
(1)从只有一个零元素的行开始,给这个 0 元素加圈,记作 ⓪ 。表示这一行所代表的人只有一种任务可派。然后把 ⓪ 所在列其他 0 元素记为 Φ \varPhi Φ 。表示该列对应任务已经指派完了,不必考虑其他人。对于( b i j b_{ij} bij),进行处理后得到如下矩阵 [ Φ 13 7 0 6 ⓪ 6 9 ⓪ 5 3 2 Φ 1 0 0 ] \begin{bmatrix} \varPhi & 13 & 7 & 0 \\ 6 & ⓪ & 6 & 9 \\ ⓪ & 5 & 3 & 2 \\ \varPhi & 1 & 0 & 0\end{bmatrix} Φ6⓪Φ13⓪5176300920 (2)给只有一个零元素的列中的零元素加 ⓪,然后把 ⓪ 所在行的零元素改为 Φ \varPhi Φ 。可得到如下矩阵: [ Φ 13 7 ⓪ 6 ⓪ 6 9 ⓪ 5 3 2 Φ 1 ⓪ Φ ] \begin{bmatrix} \varPhi & 13 & 7 & ⓪ \\ 6 & ⓪ & 6 & 9 \\ ⓪ & 5 & 3 & 2 \\ \varPhi & 1 & ⓪ & \varPhi \end{bmatrix} Φ6⓪Φ13⓪51763⓪⓪92Φ (3)反复进行(1)(2)两步,直至所有的 0 元素均被圈出或划去为止。
(4)若仍然有没有画圈的零元素,且同行(列)的 0 元素至少有两个(表示对这个可以从两项任务中指派其一)。这时可用不同的方案去试探。从剩有零元素最少的行开始,比较这行各 0 元素所在列中 0 元素的数目,选择 0 元素少的那列的这个 0 元素加圈(因为一列中零元素多,说明可派的人选择较多,我们应派可选择较少的任务),然后去掉同行同列的其他 0 元素。可反复进行,直到所有的 0 元素都已经圈出和去掉为止。
(5)若 ⓪ 元素的数目 m m m 等于矩阵的阶数 n n n ,那么这个指派问题的最优解已经找到。若 m < n m<n m<n ,则转入下一步。
Step 3: 以最少的直线覆盖所有 0 元素,确定当前系数矩阵中能找到的最多的 0 元素。按以下步骤进行:
(1)对没有 ⓪ 的行打 ✔ ;
(2)对已经打 ✔ 行中所有含有 Φ \varPhi Φ 的列打上 ✔ ;
(3)再对打有 ✔ 的列中含有 ⓪ 元素的行打 ✔ ;
(4)重复第 2,3 步,直到无法继续打 ✔ 为止;
(5)对没有打 ✔ 的行划线,对打 ✔ 的列划线。这就得到了覆盖所有 0 元素的最少直线数。若直线数 l < n l<n l<n ,说明需增加 0 元素,转下一步。
Step 4: 增加 0 元素。对第三步中没有被直线覆盖的部分中找出最小元素,然后在打 ✔ 行各元素中都减去这个最小元素,打 ✔ 列的各元素多加上这个最小元素,以保证原来的 0 元素不变。这样得到的新矩阵(和原来同解),若得到 n n n 个独立的 0 元素,则已经得到最优解,否则需回到上一步重复进行。
当指派问题的系数矩阵,经过变换得到了同行和同列中都有两个或两个以上的 0 元素,这时可以任意选取一行中的某一个 0 元素,再去掉同行中的其他 0 元素,会出现多重解。
5.3 非标准的指派问题
指派任务和待指派的人员数目相同的极小化问题称为标准的指派问题,但在实际问题中,常常遇见各种各样非标准形式的指派问题。此时我们需对其进行一定处理,转化为标准指派问题,再利用匈牙利法进行求解。
对于“任务”和“人员”数目不等的指派问题,若“人员”数 m m m 小于任务数 n n n ,则添加上 n − m n-m n−m 个虚拟“人员”,这些虚拟“人员”完成任务的“费用”为 0 。如果得到的方案中,某项目由虚拟“人员”完成,则表示该项目无人去做。若“人员”数 m m m 大于“任务”数 n n n ,则添加 m − n m-n m−n 个虚拟“任务”,这些虚拟“任务”被人员完成的“费用”也为 0 。同样,如果得到的方案中,某人员被派去完成虚拟“任务”,说明该“人员”闲了下来。
在指派问题中,如果某“人员”可以完成多项“任务”,可将该人员看成相同的多个“人员”,这几个人员完成同一项“任务”的“费用”是相同的。如果某一“人员”一定不能承担某一“任务”,则相应费用取值应为足够大的正数 M M M 。
对于极大化的指派问题,即求 max z = ∑ ∑ c i j x i j \max{z}=\sum\sum c_{ij}x_{ij} maxz=∑∑cijxij ,可令 b i j = M − c i j b_{ij}=M-c_{ij} bij=M−cij ,其中 M M M 可取 c i j c_{ij} cij 中最大数,这时系数矩阵变换为 B = ( b i j ) B=(b_{ij}) B=(bij) ,此时 b i j ≥ 0 b_{ij}\geq 0 bij≥0 ,符合匈牙利算法条件。原极大化目标函数变为 min z = ∑ ∑ b i j x i j \min{z}=\sum\sum b_{ij}x_{ij} minz=∑∑bijxij ,此最小解即为原问题的最大解。
写在最后
那到此,整数规划的理论部分就全部结束了。