前言

核心内容来自博客链接1博客连接2希望大家多多支持作者
本文记录用，防止遗忘

循环神经网络——编码器-解码器架构

课件

重新考察CNN

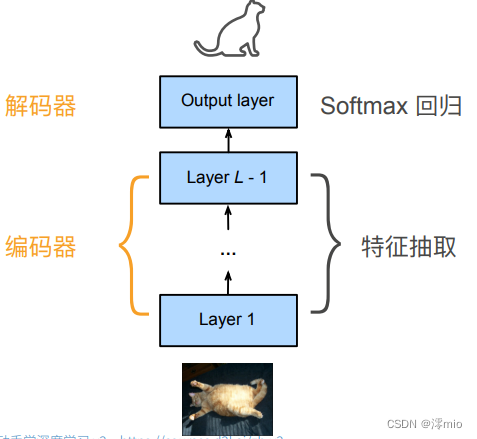
• 编码器：将输入编程成中间表达形式（特征)
• 解码器：将中间表示解码成输出

重新考察RNN

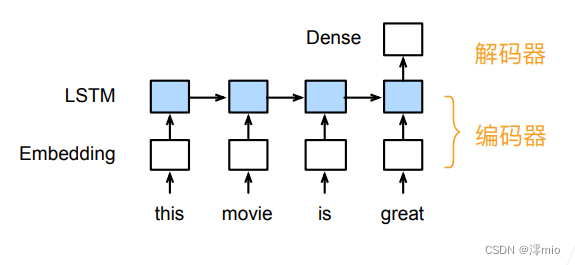
• 编码器：将文本表示成向量
• 解码器：向量表示成输出

编码器-解码器架构

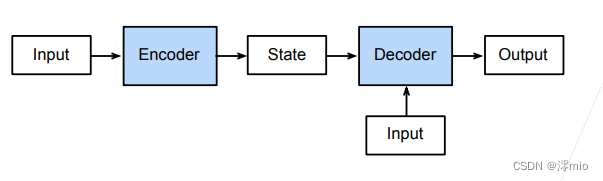
一个模型被分为两块:

• 编码器处理输入
• 解码器生成输出
  

总结

• 使用编码器-解码器架构的模型，编码器负责表示输入,解码器负责输出

教材

正如我们在上一节机器翻译数据集中所讨论的， 机器翻译是序列转换模型的一个核心问题， 其输入和输出都是长度可变的序列。 为了处理这种类型的输入和输出， 我们可以设计一个包含两个主要组件的架构： 第一个组件是一个编码器（encoder）： 它接受一个长度可变的序列作为输入， 并将其转换为具有固定形状的编码状态。 第二个组件是解码器（decoder）： 它将固定形状的编码状态映射到长度可变的序列。 这被称为编码器-解码器（encoder-decoder）架构， 如图所示。

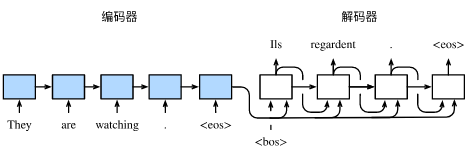
我们以英语到法语的机器翻译为例： 给定一个英文的输入序列：“They”“are”“watching”“.”。 首先，这种“编码器－解码器”架构将长度可变的输入序列编码成一个“状态”， 然后对该状态进行解码， 一个词元接着一个词元地生成翻译后的序列作为输出： “Ils”“regordent”“.”。 由于“编码器－解码器”架构是形成后续章节中不同序列转换模型的基础， 因此本节将把这个架构转换为接口方便后面的代码实现。

下图描述了使用编码器—解码器将英语句子翻译成法语句子的一种方法。在训练数据集中，我们可以在每个句子后附上特殊符号“<eos>”（end of sequence）以表示序列的终止。编码器每个时间步的输入依次为英语句子中的单词、标点和特殊符号“<eos>”。图10.8中使用了编码器在最终时间步的隐藏状态作为输入句子的表征或编码信息。解码器在各个时间步中使用输入句子的编码信息和上个时间步的输出以及隐藏状态作为输入。我们希望解码器在各个时间步能正确依次输出翻译后的法语单词、标点和特殊符号"<eos>“。需要注意的是，解码器在最初时间步的输入用到了一个表示序列开始的特殊符号”<bos>"（beginning of sequence）。

1 编码器

编码器的作用是把一个不定长的输入序列变换成一个定长的背景变量$c$，并在该背景变量中编码输入序列信息。常用的编码器是循环神经网络。

让我们考虑批量大小为1的时序数据样本。假设输入序列是$x_1,...,x_T$ ，例如$x_i$是输入句子中的第$i$个词。在时间步$t$，循环神经网络将输入$x_t$ 的特征向量$x_t$和上个时间步的隐藏状态$h_{t-1}$变换为当前时间步的隐藏状态$h_t$ 。我们可以用函数$f$表达循环神经网络隐藏层的变换：

$$h_t=f(x_t,h_t-1)$$

接下来，编码器通过自定义函数$q$将各个时间步的隐藏状态变换为背景变量。

$$c=q(h_1,...,h_T)$$
例如，当选择$q(h_1,...,h_T)=h_T$时，背景变量是输入序列最终时间步的隐藏状态$h_T$

以上描述的编码器是一个单向的循环神经网络，每个时间步的隐藏状态只取决于该时间步及之前的输入子序列。我们也可以使用双向循环神经网络构造编码器。在这种情况下，编码器每个时间步的隐藏状态同时取决于该时间步之前和之后的子序列（包括当前时间步的输入），并编码了整个序列的信息。

在编码器接口中，我们只指定长度可变的序列作为编码器的输入X。 任何继承这个Encoder基类的模型将完成代码实现。

from torch import nn

class Encoder(nn.Module):
    """编码器-解码器架构的基本编码器接口"""
    def __init__(self, **kwargs):
        super(Encoder, self).__init__(**kwargs)

    def forward(self, X, *args):
        raise NotImplementedError

2 解码器

刚刚已经介绍，编码器输出的背景变量$c$编码了整个输入序列$x_1,...,x_T$的信息。给定训练样本中的输出序列$y_1,...,y_{T^{\prime }}$，对每个时间步$t\prime$（符号与输入序列或编码器的时间步$t$有区别），解码器输出$y_{t^{\prime }}$的条件概率将基于之前的输出序列$y_1,...,y_{t^{\prime }-1}$和背景变量$c$，即$P(y_{t^{\prime }}|y_1,...,y_{t-1^{\prime }},c)$
为此，我们可以使用另一个循环神经网络作为解码器。在输出序列的时间步$t\prime$ ，解码器将上一时间步的输出$y_{t^{\prime }-1}$以及背景变量$c$作为输入，并将它们与上一时间步的隐藏状态$s_{t\prime -1}$ 变换为当前时间步的隐藏状态$s_{t\prime }$。因此，我们可以用函数$g$表达解码器隐藏层的变换：
$$s_{t^{\prime }}=g(t_{t^{\prime }-1}，c,s_{t\prime -1})$$
有了解码器的隐藏状态后，我们可以使用自定义的输出层和softmax运算来计算$P(y_{t\prime }\mid y_1,\dots ,y_{t\prime -1},c)$例如，基于当前时间步的解码器隐藏状态$s_{t\prime }$、上一时间步的输出$y_{t\prime -1}$以及背景变量$c$来计算当前时间步输出$y_{t^{\prime }}$ 的概率分布。

在下面的解码器接口中，我们新增一个init_state函数， 用于将编码器的输出（enc_outputs）转换为编码后的状态。 注意，此步骤可能需要额外的输入，例如：输入序列的有效长度。 为了逐个地生成长度可变的词元序列， 解码器在每个时间步都会将输入 （例如：在前一时间步生成的词元）和编码后的状态 映射成当前时间步的输出词元。

class Decoder(nn.Module):
    """编码器-解码器架构的基本解码器接口"""
    def __init__(self, **kwargs):
        super(Decoder, self).__init__(**kwargs)

    def init_state(self, enc_outputs, *args):
        raise NotImplementedError

    def forward(self, X, state):
        raise NotImplementedError

3 合并编码器和解码器

总而言之，“编码器-解码器”架构包含了一个编码器和一个解码器， 并且还拥有可选的额外的参数。 在前向传播中，编码器的输出用于生成编码状态， 这个状态又被解码器作为其输入的一部分。

class EncoderDecoder(nn.Module):
    """编码器-解码器架构的基类"""
    def __init__(self, encoder, decoder, **kwargs):
        super(EncoderDecoder, self).__init__(**kwargs)
        self.encoder = encoder
        self.decoder = decoder

    def forward(self, enc_X, dec_X, *args):
        enc_outputs = self.encoder(enc_X, *args)
        dec_state = self.decoder.init_state(enc_outputs, *args)
        return self.decoder(dec_X, dec_state)

“编码器－解码器”体系架构中的术语状态 会启发人们使用具有状态的神经网络来实现该架构。 在下一节中，我们将学习如何应用循环神经网络， 来设计基于“编码器－解码器”架构的序列转换模型。

4 训练模型

根据最大似然估计，我们可以最大化输出序列基于输入序列的条件概率

并得到该输出序列的损失

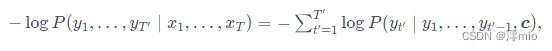
在模型训练中，所有输出序列损失的均值通常作为需要最小化的损失函数。在图所描述的模型预测中，我们需要将解码器在上一个时间步的输出作为当前时间步的输入。与此不同，在训练中我们也可以将标签序列（训练集的真实输出序列）在上一个时间步的标签作为解码器在当前时间步的输入。这叫作强制教学（teacher forcing）。

5 小结

• 编码器－解码器”架构可以将长度可变的序列作为输入和输出，因此适用于机器翻译等序列转换问题。

• 编码器将长度可变的序列作为输入，并将其转换为具有固定形状的编码状态。

• 解码器将具有固定形状的编码状态映射为长度可变的序列。

参考文献

[1] Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078.

[2] Sutskever, I., Vinyals, O., & Le, Q. V. (2014). Sequence to sequence learning with neural networks. In Advances in neural information processing systems (pp. 3104-3112).