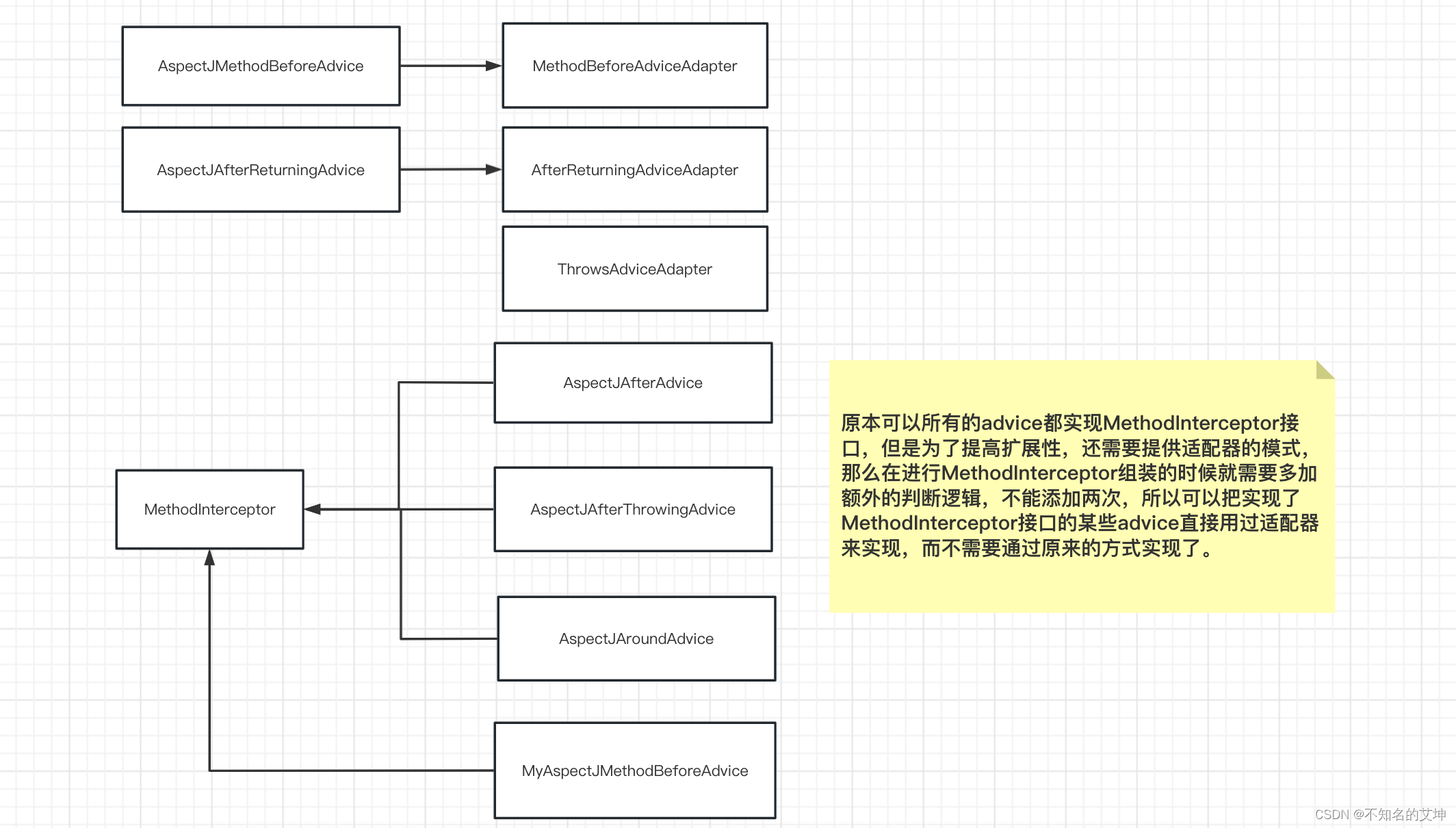
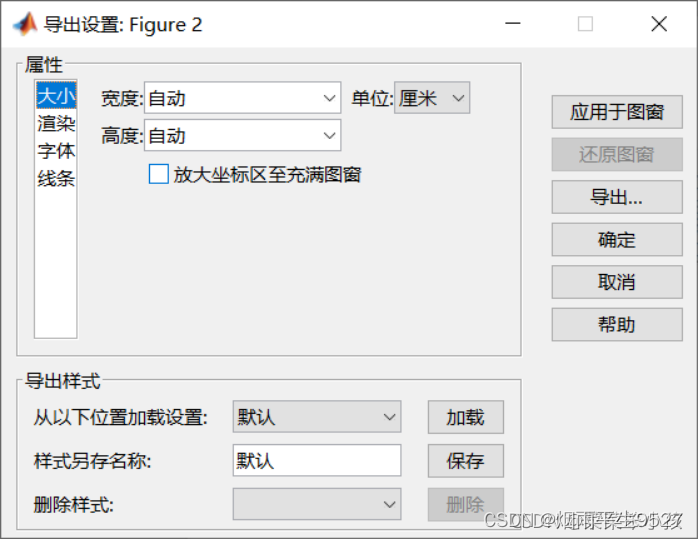
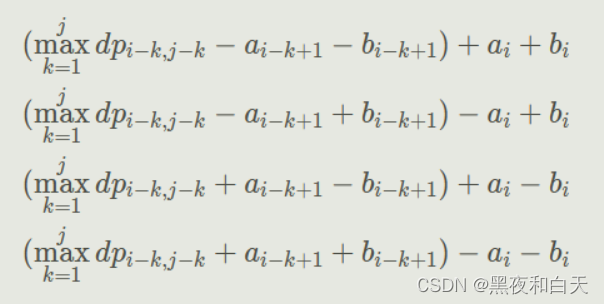1.算法目的（败者树）

解决多路平衡归并带来的问题。
在外部排序中，使用k路平衡归并策略,
选出一个最小元素需要对比关键字(k-1)次，
导致内部归并所需时间增加。（可用“败者树”进行优化）

2.败者树的定义

败者树：可视为一棵完全二叉树(多了一个头头)。
k个叶结点分别是当前参加比较的元素，
非叶子结点用来记忆左右子树中的“失败者”，
而让胜者往上继续进行比较，一直到根结点。

3.败者树在多路平衡归并中的应用

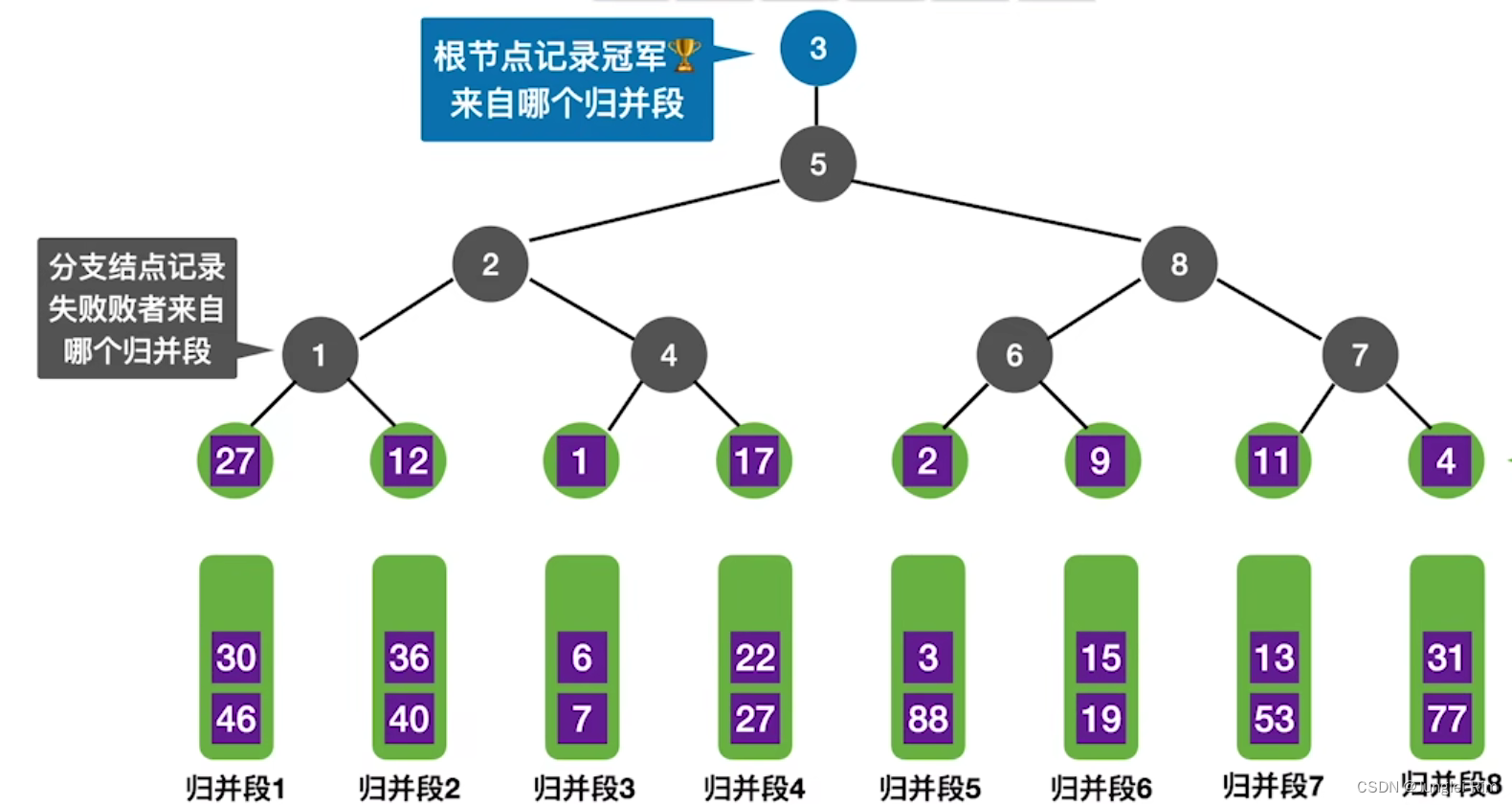
对于k路归并，第一次构造败者，树需要对比关键字k-1次。
有了败者树，选出最小元素，只需对比关键字$「lo{g}_{2}k|$次。

4.败者树的实现思路

k路归并的败者树只需要定义一个长度为k的数组即可。

5.置换选择排序

可用“置换-选择排序"进一步减少初始归并段数量.

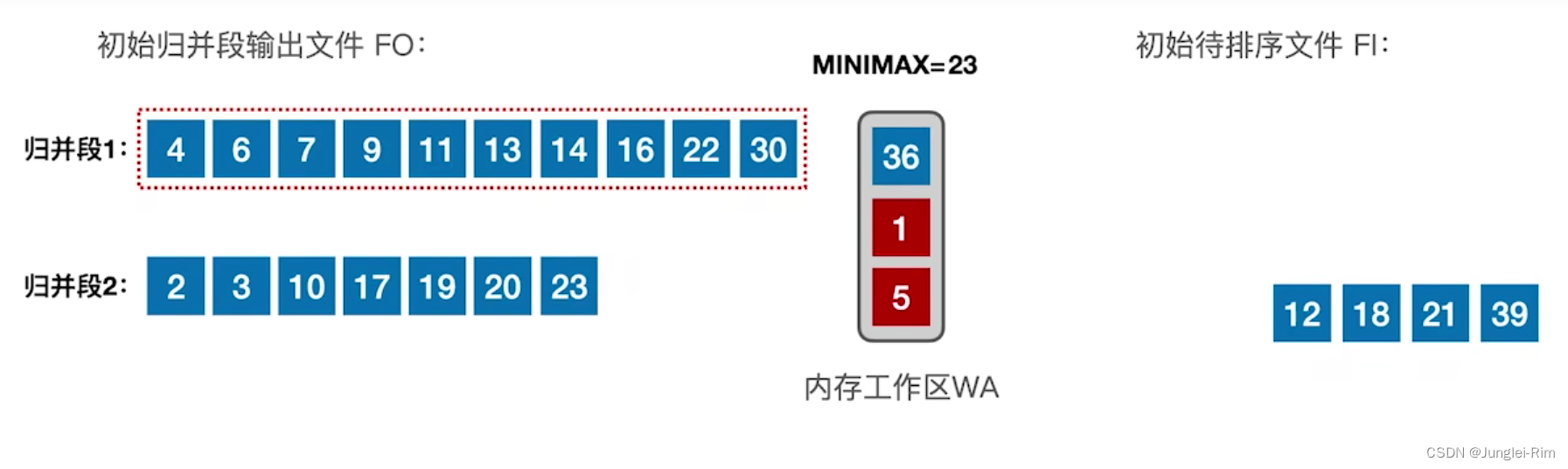
注:假设用于内部排序的内存工作区只能容纳3个记录。

若WA内的关键字都比MINIMAX更小，则该归并段在此截止.

使用置换-选择排序，
可以让每个初始归并段的长度超越内存工作区大小的限制.

1.步骤

设初始待排文件为FI，初始归并段输出文件为FO，内存工作区为WA，
FO和WA的初始状态为空，WA可容纳w个记录。
置换-选择算法的步骤如下:

1. 从FI输入w个记录到工作区WA。
2. 从WA中选出其中关键字取最小值的记录，记为MINIMAX记录。
3. 将MINIMAX记录输出到FO中去。
4. 若FI不空，则从FI输入下一个记录到WA中。
5. 从WA中所有关键字比MINIMAX记录的关键字大的记录中选出最小关键字记录，作为新的MINIMAX记录。
6. 重复3~5，直至在WA中选不出新的MINIMAX记录为止，由此得到一个初始归并段，输出一个归并段的结束标志到FO中去。
7. 重复2~6，直至WA为空。由此得到全部初始归并段。