五、回溯（trackback）

news2024/12/28 4:44:42

文章目录

  • 一、算法定义
  • 二、经典例题
    • （一）排列
      • 1.[46.全排列](https://leetcode.cn/problems/permutations/description/)
        • （1）思路
        • （2）代码
        • （3）复杂度分析
      • 2.[LCR 083. 全排列](https://leetcode.cn/problems/VvJkup/description/)
        • （1）思路
        • （2）代码
        • （3）复杂度分析
      • 3.[46.全排列2](https://leetcode.cn/problems/permutations-ii/description/)
      • （1）思路
      • （2）代码
      • （3）复杂度分析
    • （二）组合
      • 1.[77.组合](https://leetcode.cn/problems/combinations/)
      • （1）思路
      • （2）代码
      • 2.[39.组合总和](https://leetcode.cn/problems/combination-sum/)
      • （1）思路
      • （2）代码
      • （3）复杂度分析
      • 3.[40.组合总和2](https://leetcode.cn/problems/combination-sum-ii/description/)
      • （1）思路
      • （2）代码
      • （3）复杂度分析
      • 4.[216.组合总和3](https://leetcode.cn/problems/combination-sum-iii/)
      • （1）思路
      • （2）代码
      • 5.[17.电话号码的字母组合](https://leetcode.cn/problems/letter-combinations-of-a-phone-number/description/)
      • （1）思路
      • （2）代码
      • （3）复杂度分析
    • （三）子集
      • 1.[78.子集](https://leetcode.cn/problems/subsets/description/)
      • （1）思路
      • （2）代码
      • （3）复杂度分析
      • 2.[131.分割回文串](https://leetcode.cn/problems/palindrome-partitioning/solutions/640336/131-fen-ge-hui-wen-chuan-hui-su-sou-suo-yp2jq/)
      • （1）思路
      • （2）代码
      • （3）复杂度分析
      • 3.[93.复原IP地址](https://leetcode.cn/problems/restore-ip-addresses/description/)
      • （1）思路
      • （2）代码
      • （3）复杂度分析
      • 4.[90.子集 II](https://leetcode.cn/problems/subsets-ii/description/)
      • （1）思路
      • （2）代码
      • （3）复杂度分析
      • 5.[491.递增子序列](https://leetcode.cn/problems/non-decreasing-subsequences/description/)
    • （四）N皇后问题、岛屿问题
      • 1.[51.N皇后](https://leetcode.cn/problems/n-queens/)
      • （1）思路
      • （2）代码
      • （3）复杂度分析

一、算法定义

抽象地说，解决一个回溯问题，实际上就是遍历一棵决策树的过程，树的每个叶子节点存放着一个合法答案。你把整棵树遍历一遍，把叶子节点上的答案都收集起来，就能得到所有的合法答案。
站在回溯树的一个节点上，你只需要思考 3 个问题：
1、路径：也就是已经做出的选择。
2、选择列表：也就是你当前可以做的选择。
3、结束条件：也就是到达决策树底层，无法再做选择的条件。
在这里插入图片描述

二、经典例题

（一）排列

1.46.全排列

（1）思路

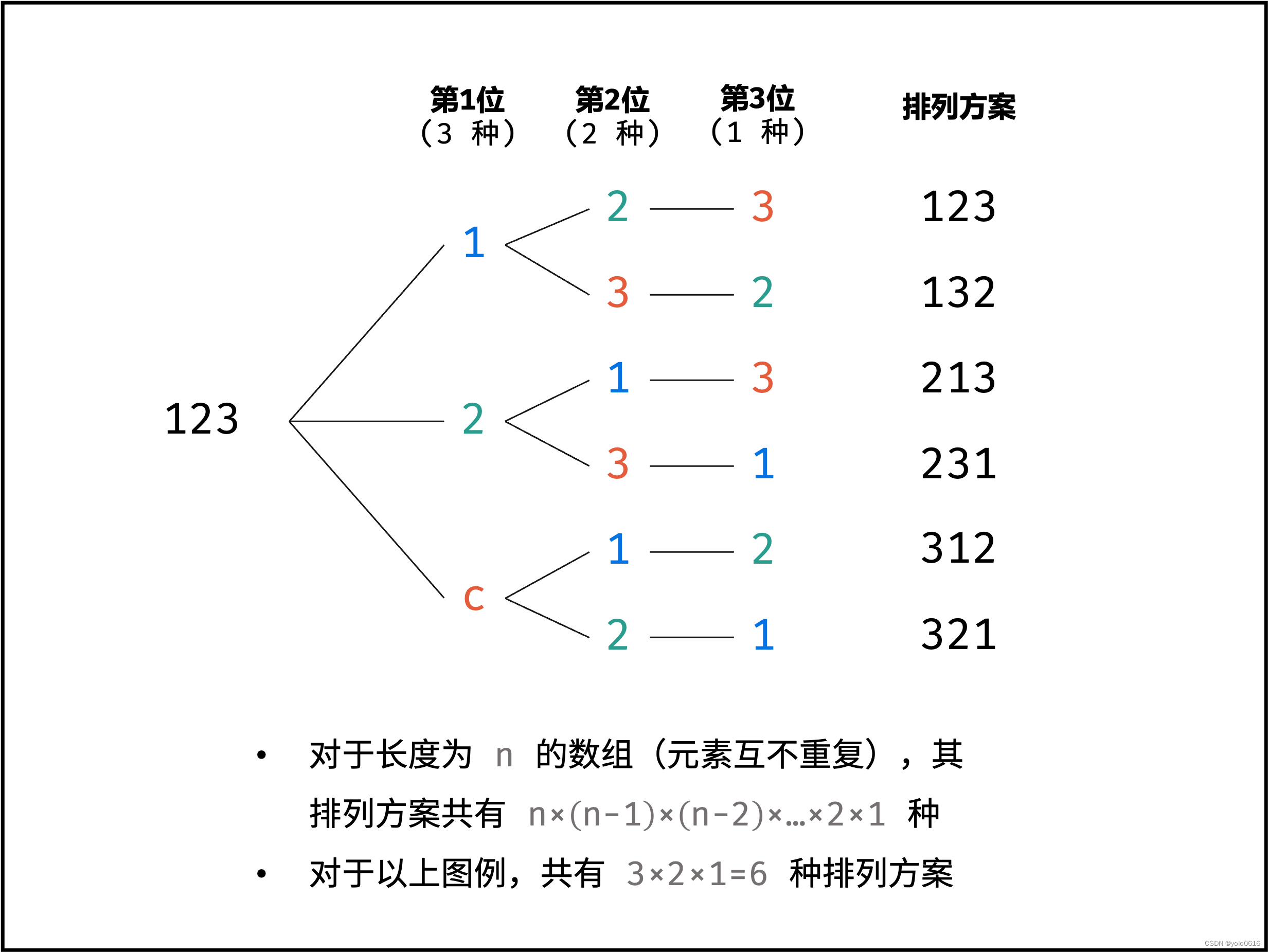
在这里插入图片描述

（2）代码
class Solution {
public:
vector<vector<int>> res;
    void dfs(vector<int>& nums) {
        vector<int> path;
        vector<bool> used(nums.size(),false);
        trackback(nums,path,used);
    }
    void trackback(vector<int>& nums,vector<int>&path,vector<bool>&used) {
        if (path.size() == nums.size()) {
            res.push_back(path);
            return ;
        }
        for (int i = 0; i < nums.size(); i ++) {
            if (used[i] == true) continue;
            path.push_back(nums[i]);
            used[i] = true;
            trackback(nums, path, used);
            used[i] = false;
            path.pop_back();
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        if (nums.size() == 0) return res;
        dfs(nums);
        return res;
    }
};
（3）复杂度分析

时间复杂度：O(n x n!)
空间复杂度：O(n),其中n为序列的长度。除答案数组以外，递归函数在递归过程中需要为每一层递归函数分配栈空间，所以这里需要额外的空间且该空间取决于递归的深度，这里可知递归调用深度为 O(n)。

2.LCR 083. 全排列

（1）思路
（2）代码
class Solution {
public:
vector<vector<int>> res;
    void process(vector<int>& nums) {
        vector<int> path;
        vector<bool> used(nums.size(),false);
        dfs(used,path,nums);

    }
    void dfs(vector<bool>& used,vector<int> &path,vector<int>& nums) {
        if (path.size() == nums.size())
        {

            res.push_back(path);
            return;
        }
        for (int i = 0; i < nums.size(); i++) {
            if (used[i]) continue;
            path.push_back(nums[i]);
            used[i] = true;
            dfs(used,path,nums);
            used[i] = false;
            path.pop_back();
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        if (nums.size() == 0) return res;
        sort(nums.begin(),nums.end());
        process(nums);

        return res;
    }
};
（3）复杂度分析

时间复杂度：O(n x n!)
空间复杂度：O(n)

3.46.全排列2

（1）思路

（2）代码

class Solution {
public:
vector<vector<int>> res;
vector<int> path;
    void process(vector<int>& nums) {
        vector<bool> used(nums.size(),false);
        trackback(nums,used);
        
    }
    void trackback(vector<int>& nums,vector<bool>& used) {
        if (path.size() == nums.size()) {
            res.push_back(path); 
            return; 
        }
        for (int i = 0; i < nums.size(); i ++) {
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) continue;
            if (used[i] == false) {
            path.push_back(nums[i]);
            used[i] = true;
            trackback(nums, used);
            path.pop_back();
            used[i] = false;
            }
        }
    }
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        if (nums.size() == 0) return res;
        sort(nums.begin(),nums.end());
        process(nums);
        return res;
    }
};

（3）复杂度分析

// 时间复杂度: 最差情况所有元素都是唯一的。复杂度和全排列1都是 O(n! * n) 对于 n 个元素一共有 n! 中排列方案。而对于每一个答案，我们需要 O(n) 去复制最终放到 result 数组
// 空间复杂度: O(n) 回溯树的深度取决于我们有多少个元素

（二）组合

1.77.组合

（1）思路

前序位置，每个节点的值都是一个子集。

（2）代码

class Solution {
public:
vector<vector<int>> res;
vector<int> path;
    void trackback(int n,int k,int start) {
        if (path.size() == k) {
            res.push_back(vector<int>(path.begin(), path.end()));
            return ;
        }
        for (int i = start;i <= n; i++) {
            path.push_back(i);
            trackback(n, k, i + 1);
            path.pop_back();
        }
    }
    vector<vector<int>> combine(int n, int k) {
        if(n == 0) return res;
        trackback(n,k,1);
        return res;
    }
};

2.39.组合总和

（1）思路

（2）代码

class Solution {
public:
vector<vector<int>>res;
vector<int> path;
    void backtrack(vector<int>& candidates,int target,int sum,int start) {
        if (sum == target) {
            res.push_back(path);
            return ;
        }
        for (int i = start; i < candidates.size() && sum + candidates[i] <= target; i++) {
        
            
            sum += candidates[i];
            path.push_back(candidates[i]);
            backtrack(candidates, target, sum,i);
            sum -= candidates[i];
            path.pop_back();
        }
    }
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        if (candidates.size() == 0) return res;
        sort(candidates.begin(), candidates.end()); // 需要排序
        backtrack(candidates,target,0,0);    
        return res;
    }

};

（3）复杂度分析

时间复杂度: O(n * 2^n)，注意这只是复杂度的上界，因为剪枝的存在，真实的时间复杂度远小于此
空间复杂度: O(target)

3.40.组合总和2

（1）思路

（2）代码

class Solution {
public:
vector<vector<int>> res;
vector<int> path;

    void trackback(vector<int>& candidates, int target,int sum,int start,vector<bool> &used) {
        if (sum == target) {res.push_back(path);return;}
        for (int i = start; i < candidates.size() && sum + candidates[i] <= target; i++) {
            if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) continue;
        
            sum += candidates[i];
            used[i] = true;
            path.push_back(candidates[i]);
            trackback(candidates, target, sum, i + 1,used);
            used[i] = false;
            sum -= candidates[i];
            path.pop_back();
        }
    }
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        if (candidates.size() == 0) return res;
        vector<bool> used(candidates.size(), false);
        sort(candidates.begin(), candidates.end());
        trackback(candidates,target,0,0,used);
        return res;
    }
};

（3）复杂度分析

时间复杂度: O(n * 2^n)，注意这只是复杂度的上界，因为剪枝的存在，真实的时间复杂度远小于此
空间复杂度: O(n)

4.216.组合总和3

（1）思路

（2）代码

class Solution {
public:
vector<vector<int>> res;
vector<int> path;
    void trackback(int k,int n,int index,int sum) {
        if (path.size() == k) {
            if (sum == n) res.push_back(path);
            return ;
        }
        for (int i = index; i <= 9 -(k - path.size()) + 1; i++) {
            sum += i;
            path.push_back(i);
            if (sum > n) {
                sum -= i;
                path.pop_back();
                return ;
            }
            trackback(k, n, i + 1,sum);
            path.pop_back();
            sum -= i;
        }
    }
    vector<vector<int>> combinationSum3(int k, int n) {
        if (n == 0) return res;
        trackback(k,n,1,0);
        return res;
    }
};

5.17.电话号码的字母组合

（1）思路

（2）代码

class Solution {
public:
const string letterMap[10] = {
        "", // 0
        "", // 1
        "abc", // 2
        "def", // 3
        "ghi", // 4
        "jkl", // 5
        "mno", // 6
        "pqrs", // 7
        "tuv", // 8
        "wxyz", // 9
};
vector<string> result;
string s;
    void backtracking(const string  &digits,int index) {
        if (index == digits.size()) {
            result.push_back(s);
            return ;
        }
        int digit = digits[index] - '0';
        string letters = letterMap[digit];
        for (int i = 0; i < letters.size(); i++) {
            s.push_back(letters[i]);

            backtracking(digits, index + 1);
            s.pop_back();
        }
    }

    vector<string> letterCombinations(string digits) {
        s.clear();
        result.clear();
        if (digits.size() == 0) {
            return result;
        }
        backtracking(digits, 0);
        return result;
    }
};

（3）复杂度分析

时间复杂度: O(3^m * 4^n)，其中 m 是对应四个字母的数字个数，n 是对应三个字母的数字个数
空间复杂度: O(3^m * 4^n)

（三）子集

1.78.子集

（1）思路

还是以 nums = [1,2,3] 为例，刚才让你求所有子集，就是把所有节点的值都收集起来；现在你只需要把第 2 层（根节点视为第 0 层）的节点收集起来，就是大小为 2 的所有组合。

（2）代码

class Solution {
public:
vector<vector<int>> res;
vector<int> path;
    vector<vector<int>> subsets(vector<int>& nums) {
        backtrack(nums,0);
        return res;
    }
    void backtrack(vector<int>& nums,int start) {
        res.push_back(path);

        for (int i = start; i < nums.size(); i ++) {
            path.push_back(nums[i]);
            backtrack(nums, i + 1);
            path.pop_back();
        }
    }
};

（3）复杂度分析

时间复杂度：O(n×2n)。一共 2n个状态，每种状态需要 O(n)的时间来构造子集。
空间复杂度：O(n)，临时数组 t 的空间代价是 O(n），递归时栈空间的代价为 O(n)。

class Solution {
public:
vector<vector<int>> res;
vector<int> path;
    void trackback(int n,int k,int start) {
        if (path.size() == k) {
            res.push_back(vector<int>(path.begin(), path.end()));
            return ;
        }
        for (int i = start;i <= n; i++) {
            path.push_back(i);
            trackback(n, k, i + 1);
            path.pop_back();
        }
    }
    vector<vector<int>> combine(int n, int k) {
        if(n == 0) return res;
        trackback(n,k,1);
        return res;
    }
};

2.131.分割回文串

（1）思路

切割问题，有不同的切割方式
判断回文

（2）代码

class Solution {
public:
vector<vector<string>> res;
vector<string> path;
    void backtrack(string s,int start) {
        if (start >= s.size()) { // 如果起始位置已经大于s的大小，说明已经找到了一组分割方案了
            res.push_back(path);
            return ;
        }   
        for (int i = start; i < s.size(); i ++) {
            if (isVaild(s,start,i)) {
                string str = s.substr(start,i - start + 1);
                path.push_back(str);
            }
            else {
                continue;
            }
            backtrack(s, i + 1); // 寻找i+1为起始位置的子串
            path.pop_back();
        }
      
    }
    bool isVaild(const string& s, int start, int end) {
     for (int i = start, j = end; i < j; i++, j--) {
         if (s[i] != s[j]) {
             return false;
         }
     }
     return true;
 }
    vector<vector<string>> partition(string s) {
        if (s.size() == 0) return res;
        backtrack(s,0);
        return res;
    }
};

（3）复杂度分析

时间复杂度: O(n * 2^n)
空间复杂度: O(n^2)

class Solution {
public: 
vector<string> res;
string path;
    void backtrack(string &s,int start,int pointSum) {
        if (pointSum == 3) {
            if (inVaild(s,start, s.size() - 1)) {
                res.push_back(s);
            }
            return ;
        }
        for (int i = start;i < s.size(); i++) {
            if (inVaild(s,start,i)) {
                 s.insert(s.begin() + i + 1 , '.');
                 pointSum ++;
                 backtrack(s, i + 2, pointSum);
                 pointSum --;
                 s.erase(s.begin() + i + 1);      
            }
            else  break;
        }
    }
    bool inVaild(const string & s,int start,int end) {
        if (start > end) {
            return false;
        }
        if (s[start] == '0' && start != end) {
            return false;
        }
        int num = 0;
        for (int i = start; i <= end; i++) {
            if (s[i] > '9' || s[i] < '0') {
            return false;
            }
            num = num * 10 + (s[i] - '0');
            if (num > 255)
                return false;
            }   
       return true;
    }   
    vector<string> restoreIpAddresses(string s) {
        if (s.size() == 0) return res;
        backtrack(s,0,0);
        return res;
    }
};

3.93.复原IP地址

（1）思路

（2）代码

class Solution {
public: 
vector<string> res;
string path;
    void backtrack(string &s,int start,int pointSum) {
        if (pointSum == 3) {
            if (inVaild(s,start, s.size() - 1)) {
                res.push_back(s);
            }
            return ;
        }
        for (int i = start;i < s.size(); i++) {
            if (inVaild(s,start,i)) { // 判断 [startIndex,i] 这个区间的子串是否合法
                 s.insert(s.begin() + i + 1 , '.'); // 在i的后面插入一个逗点
                 pointSum ++;
                 backtrack(s, i + 2, pointSum); //  插入逗点之后下一个子串的起始位置为i+2
                 pointSum --;
                 s.erase(s.begin() + i + 1);    //回溯删掉逗点
            }
            else  break;
        }
    }
    bool inVaild(const string & s,int start,int end) {
        if (start > end) {
            return false;
        }
        if (s[start] == '0' && start != end) {
            return false;
        }
        int num = 0;
        for (int i = start; i <= end; i++) {
            if (s[i] > '9' || s[i] < '0') {
            return false;
            }
            num = num * 10 + (s[i] - '0');
            if (num > 255)
                return false;
            }   
       return true;
    }   
    vector<string> restoreIpAddresses(string s) {
        if (s.size() == 0) return res;
        backtrack(s,0,0);
        return res;
    }
};

（3）复杂度分析

  • 时间复杂度: O(3^4)，IP地址最多包含4个数字，每个数字最多有3种可能的分割方式，则搜索树的最大深度为4，每个节点最多有3个子节点。
  • 空间复杂度: O(n)

4.90.子集 II

（1）思路

（2）代码

class Solution {
public:
vector<vector<int>> res;
vector<int> path;
 void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
     res.push_back(path);
     for (int i = startIndex; i < nums.size(); i++) {
          if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                continue;
            }
            path.push_back(nums[i]);
            used[i] = true;
            backtracking(nums, i + 1, used);
            used[i] = false;
            path.pop_back();
     }
}
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        res.clear();
        path.clear();
        vector<bool> used(nums.size(), false);
        sort(nums.begin(), nums.end()); // 去重需要排序
        backtracking(nums, 0, used);
        return res;
    }
};

（3）复杂度分析

  • 时间复杂度: O(n * 2^n)
  • 空间复杂度: O(n)

5.491.递增子序列

class Solution {
public:
vector<vector<int>> res;
vector<int> path;
    void backtrack(vector<int>&nums,int start) {
        if (path.size() > 1) {
            res.push_back(path);
    // 注意这里不要加return，因为要取树上的所有节点
        }
        unordered_set<int> uset; // 使用set对本层元素进行去重
        for (int i = start; i < nums.size(); i ++ ) {
            if ((!path.empty() && nums[i] < path.back())
                    || uset.find(nums[i]) != uset.end()) {
                    continue;
            }
            uset.insert(nums[i]); // 记录这个元素在本层用过了，本层后面不能再用了
            path.push_back(nums[i]);
            backtrack(nums, i + 1);
            path.pop_back();
        }
    }
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        if (nums.size() == 0) return res;
        
        backtrack(nums,0);
        return res;
    }
};

（四）N皇后问题、岛屿问题

1.51.N皇后

（1）思路

（2）代码

class Solution {
public:
vector<vector<string>> res;
    vector<vector<string>> solveNQueens(int n) {
        vector<string> board (n,string(n,'.'));
        backtrack(board,0);
        return res;
    }
    void backtrack(vector<string>& board, int row) {
        if (row == board.size()) {
            res.push_back(board);
            return;
        }
        int n = board[row].size();
        for (int col = 0; col < n; col++) {
            if (!isvaild(board,row,col)) {
                continue;
            }
            board[row][col] = 'Q';
             backtrack(board, row + 1);
            // 撤销选择
            board[row][col] = '.';
        }
    }
    bool isvaild(vector<string>& board, int row, int col) {
        int n = board.size();
        for (int i = 0; i <= row; i++) {
            if (board[i][col] == 'Q')
                return false;
        }
        for (int i = row - 1,j = col + 1; i >= 0 && j < n;i --,j ++) { // 左上
            if (board[i][j] == 'Q')
            return false;
        }
        for (int i = row - 1, j = col - 1;i >= 0 && j >= 0; i--, j--) {  // 右上
            if (board[i][j] == 'Q')
            return false;
        }
        return true;
    }
};

（3）复杂度分析

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1050010.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

优优嗨聚集团：美团代运营服务，对美团外卖商家有何促进

优优嗨聚集团：美团代运营服务，对美团外卖商家有何促进

美团代运营服务一直是美团外卖商家成功的关键因素之一。美团代运营服务是一种专业的营销服务&#xff0c;它可以帮助商家在美团平台上更好地经营和销售&#xff0c;从而提高店铺曝光率、提升用户评价、提高营收等方面的水平。 首先&#xff0c;美团代运营服务可以帮助商家提高店…
阅读更多...
4.canvas绘制基本图形——折线

4.canvas绘制基本图形——折线

在日常生活中&#xff0c;除了矩形与圆弧外&#xff0c;接触最多的就是折线了。甚至矩形也可以看出是一段折线&#xff0c;所以我们自然也可以使用绘制折线的方式绘制出矩形 moveTo 认识折线之前&#xff0c;我们先认识下moveTo这个方法。形象一点说这个方法就是将我们的画笔…
阅读更多...
Leetcode 1239. 串联字符串的最大长度

Leetcode 1239. 串联字符串的最大长度

文章目录 题目代码&#xff08;9.29 首刷部分看解析&#xff09; 题目 Leetcode 1239. 串联字符串的最大长度 代码&#xff08;9.29 首刷部分看解析&#xff09; class Solution { public:unordered_set<int> skip;unordered_set<char> used;int maxLength(vecto…
阅读更多...
常见的7种分布式解决方案(2pc,3pc,Tcc,Seta、本地事务....)

常见的7种分布式解决方案(2pc,3pc,Tcc,Seta、本地事务....)

一 分布式事务 1.1 分布式事务 在分布式系统中一次操作需要由多个服务协同完成&#xff0c;这种由不同的服务之间通过网络协同完成的事务称为分布式事务。 1.首先满足事务特性&#xff1a;ACID 2.而在分布式环境下&#xff0c;会涉及到多个数据库 总结&#xff1a;分布式事务…
阅读更多...
搭建自己的搜索引擎之三

搭建自己的搜索引擎之三

一、前言 接上一篇 搭建自己的搜索引擎之二&#xff0c;本篇主要讲一下我们如何操作ElasticSearch&#xff0c;就是最简单的增删改查命令怎么写。 二、几个概念 搭建自己的搜索引擎之一 这篇文章我们对比搜索引擎在做海量数据实时查询优于关系型数据库的一些原因&#xff0c…
阅读更多...
山西电力市场日前价格预测【2023-09-29】

山西电力市场日前价格预测【2023-09-29】

日前价格预测 预测说明&#xff1a; 如上图所示&#xff0c;预测明日&#xff08;2023-09-29&#xff09;山西电力市场全天平均日前电价为189.30元/MWh。其中&#xff0c;最高日前电价为338.58元/MWh&#xff0c;预计出现在18: 45。最低日前电价为0.00元/MWh&#xff0c;预计出…
阅读更多...
V4L2 驱动架构介绍

V4L2 驱动架构介绍

V4L2 简介 Video for Linux two(Video4Linux2)简称 V4L2&#xff0c;是 V4L 的改进版。V4L2 是 linux操作系统下用于视频和音频数据采集设备的驱动框架&#xff0c;为驱动和应用程序提供了一套统一的接口规范。 在 Linux 下&#xff0c;所有外设都被看成一种特殊的文件&#xf…
阅读更多...
重大发布 | 雷特百元级DALI主控 200场景·万灯独控·有线无线全覆盖

重大发布 | 雷特百元级DALI主控 200场景·万灯独控·有线无线全覆盖

中秋国庆放假安排 喜迎国庆、欢度中秋。按照国家有关规定&#xff0c;智哪儿定于9.29-10.6期间放假&#xff0c;10.7-10.8正常上班。 假期期间&#xff0c;智哪儿全平台暂停更新。祝大家合理安排好假期生活&#xff0c;度过一个愉快的假期。
阅读更多...
力扣 -- 115. 不同的子序列

力扣 -- 115. 不同的子序列

解题步骤&#xff1a; 参考代码&#xff1a; class Solution { public:int numDistinct(string s, string t) {int ns.size();int mt.size();//多开一行&#xff0c;多开一列vector<vector<double>> dp(m1,vector<double>(n1));for(size_t j0;j<n;j){dp[…
阅读更多...
嵌入式开源库之libmodbus学习笔记

嵌入式开源库之libmodbus学习笔记

socat 安装sudo apt-get install socat创建终端 socat -d -d pty,b115200 pty,b115200查看终端 ls /dev/pts/ minicom 安装 sudo apt-get install minicom链接虚拟终端 sudo minicom -D /dev/pts/3以十六进制显示 minicom -D /dev/pts/1 -H设置波特率 minicom -D /dev/pts/1…
阅读更多...
【神经网络可视化】 梯度上升，可视化工具，风格转移

【神经网络可视化】 梯度上升，可视化工具，风格转移

可视化可以帮助我们更好的理解卷积网络每一层学到了什么&#xff0c;或者说每一个卷积核究竟学到了什么&#xff0c;他是怎么理解图像的 这种的话当我们神经网络结果不太好时&#xff0c;我们可以分析不好的原因 图片来源于李飞飞老师的内容 梯度上升方法做可视化 文章目录 …
阅读更多...
Spring整合第三方框架-MyBatis整合Spring实现

Spring整合第三方框架-MyBatis整合Spring实现

Spring整合MyBatis的步骤 导入MyBatis整合Spring相关坐标。 <dependency><groupId>org.mybatis</groupId><artifactId>mybatis-spring</artifactId><version>2.0.5</version></dependency><dependency><groupId>…
阅读更多...
Docker下如何构建包含延迟插件的RabbitMQ镜像

Docker下如何构建包含延迟插件的RabbitMQ镜像

&#x1f468;&#x1f3fb;‍&#x1f4bb; 热爱摄影的程序员 &#x1f468;&#x1f3fb;‍&#x1f3a8; 喜欢编码的设计师 &#x1f9d5;&#x1f3fb; 擅长设计的剪辑师 &#x1f9d1;&#x1f3fb;‍&#x1f3eb; 一位高冷无情的编码爱好者 大家好&#xff0c;我是 DevO…
阅读更多...
低温结霜可视化实验装置的真空压力精密控制技改方案

低温结霜可视化实验装置的真空压力精密控制技改方案

摘要&#xff1a;低温结霜可视化实验装置主要用于模拟空间环境并研究深冷表面结霜现象&#xff0c;客户希望对现有实验装置的真空系统进行技术升级&#xff0c;以实现0.001Pa~1000Pa范围内真空度的准确控制。为此本文提出了分段控制解决方案&#xff0c;即采用电容真空计、电动…
阅读更多...
04. 人工智能核心基础 - 导论（3）

04. 人工智能核心基础 - 导论（3）

文章目录 人工智能和其他学科的关系为什么学习人工智能怎么学好人工智能&#xff1f;一些问题 Hi&#xff0c;你好。我是茶桁。 基于上一节课咱们的整体强度有点大&#xff0c;而且咱们马上也要进入高强度内容了&#xff0c;那么这一篇咱们就稍微水一篇吧。来聊聊天&#xff0…
阅读更多...
publicPath：打包时的配置

publicPath：打包时的配置

vue项目&#xff0c;执行打包命令后&#xff0c;会在项目的根目录中自动创建一个文件夹dist,dist中的文件就是打包后的文件&#xff0c;只需要放到服务器中即可。 【默认情况下&#xff0c;用的绝对路径&#xff0c;需要放到服务器的根目录打开。】 如果希望放到子目录也能运行…
阅读更多...
Stm32_标准库_4_TIM中断_PWM波形_呼吸灯

Stm32_标准库_4_TIM中断_PWM波形_呼吸灯

基本原理 PWM相关物理量的求法 呼吸灯代码 #include "stm32f10x.h" // Device header #include "Delay.h"TIM_TimeBaseInitTypeDef TIM_TimeBaseInitStructure; TIM_OCInitTypeDef TIM_OCInitStructuer;//结构体 GPIO_InitTypeDef GPIO_InitStructur…
阅读更多...
Linux C/C++下收集指定域名的子域名信息（类似dnsmap实现）

Linux C/C++下收集指定域名的子域名信息（类似dnsmap实现）

我们知道dnsmap是一个工具&#xff0c;主要用于收集指定域名的子域名信息。它对于渗透测试人员在基础结构安全评估的信息收集和枚举阶段非常有用&#xff0c;可以帮助他们发现目标公司的IP网络地址段、域名等信息。 dnsmap的操作原理 dnsmap&#xff08;DNS Mapping&#xff…
阅读更多...
nodejs基于Vue.js健身体育器材用品商城购物网97794

nodejs基于Vue.js健身体育器材用品商城购物网97794

管理员端的功能主要是开放给系统的管理人员使用&#xff0c;能够对用户的信息进行管理&#xff0c;包括对用户、健身器材、器材类型、系统和订单进行查看&#xff0c;修改和删除、新增等&#xff0c;对系统整体运行情况进行了解。用户的功能主要是对个人账号和密码进行更新信息…
阅读更多...
26659-2011 铸造用再生硅砂 课堂随笔

26659-2011 铸造用再生硅砂 课堂随笔

声明 本文是学习GB-T 26659-2011 铸造用再生硅砂. 而整理的学习笔记,分享出来希望更多人受益,如果存在侵权请及时联系我们 1 范围 本标准规定了铸造用再生硅砂的术语和定义、分级及牌号、技术要求、试验方法、检验规则以及包 装、标志、运输和储存等要求。 本标准适用于铸…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023