欢迎关注我的CSDN：https://spike.blog.csdn.net/
本文地址：https://spike.blog.csdn.net/article/details/133378367

在模型训练中，如果出现 NaN 的问题，严重影响 Loss 的反传过程，因此，需要加入一些微小值进行处理，避免影响模型的训练结果。

例如，交叉熵损失 sigmoid_cross_entropy，包括对数函数(log) ，当计算 log 值时，当输入为0时，则会导致溢出，因此，需要加入极小值 (例如 1e-8) 约束，避免溢出。

交叉熵公式：

$$L(y,\hat{y})=-\frac{1}{N}\sum _{i=1}^N[y_i\log ({\hat{y}}_i)+(1-y_i)\log (1-{\hat{y}}_i)]$$

Log 曲线：

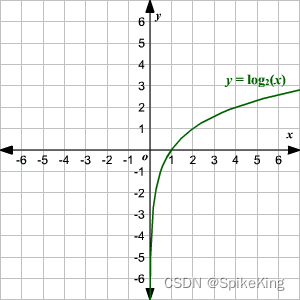
即：

# 额外增加 eps，可以避免数值溢出
def sigmoid_cross_entropy(logits, labels, eps=1e-8):
    logits = logits.float()
    log_p = torch.log(torch.sigmoid(logits)+eps)
    log_not_p = torch.log(torch.sigmoid(-logits)+eps)
    loss = -labels * log_p - (1 - labels) * log_not_p
    return loss

Sigmoid Cross Entropy 是一种常用的损失函数，用于衡量二分类问题中模型的预测结果和真实标签之间的差异，作用是优化模型的参数，使得模型能够更好地拟合数据，提高分类的准确性。

参考：How to solve the loss become nan because of using torch.log()