迪杰斯特拉算法
- Dijkstra 算法是一种广泛使用的算法,用于查找图中的最短路径。
- 它通过从起始节点迭代选择成本最小的节点来探索搜索空间。
- Dijkstra 算法计算到达每个节点的成本,并在找到更短路径时更新成本。
- 它会持续下去,直到到达目标节点或探索完所有可到达的节点。
公式
- math.hypot()
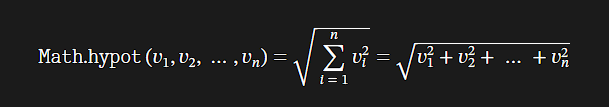
- math.sqrt()
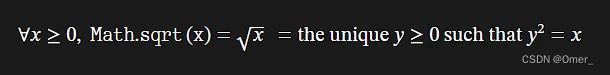
import matplotlib.pyplot as plt
import math
class Dijkstra:
def __init__(self, ox, oy, resolution, robot_radius):
"""
Initialize map for a star planning
ox: x position list of Obstacles [m]
oy: y position list of Obstacles [m]
resolution: grid resolution [m]
rr: robot radius[m]
"""
self.min_x = None
self.min_y = None
self.max_x = None
self.max_y = None
self.x_width = None
self.y_width = None
self.obstacle_map = None
self.resolution = resolution
self.robot_radius = robot_radius
self.calc_obstacle_map(ox, oy)
self.motion = self.get_motion_model()
class Node:
def __init__(self, x, y, cost, parent_index):
self.x = x # index of grid
self.y = y # index of grid
self.cost = cost
# self.grid = grid
self.parent_index = parent_index # index of previous Node
def __str__(self):
return str(self.x) + "," + str(self.y) + "," + str(
self.cost) + "," + str(self.parent_index)
def planning(self, sx, sy, gx, gy):
"""
dijkstra path search
input:
s_x: start x position [m]
s_y: start y position [m]
gx: goal x position [m]
gx: goal x position [m]
output:
rx: x position list of the final path
ry: y position list of the final path
"""
start_node = self.Node(self.calc_xy_index(sx, self.min_x),
self.calc_xy_index(sy, self.min_y), 0.0, -1)
goal_node = self.Node(self.calc_xy_index(gx, self.min_x),
self.calc_xy_index(gy, self.min_y), 0.0, -1)
open_set, closed_set = dict(), dict()
open_set[self.calc_index(start_node)] = start_node
while True:
c_id = min(open_set, key=lambda o: open_set[o].cost)
current = open_set[c_id]
# show graph
if show_animation == True # pragma: no cover
plt.plot(self.calc_position(current.x, self.min_x),
self.calc_position(current.y, self.min_y), "xc")
# for stopping simulation with the esc key.
plt.gcf().canvas.mpl_connect(
'key_release_event',
lambda event: [exit(0) if event.key == 'escape' else None])
if len(closed_set.keys()) % 10 == 0:
plt.pause(0.001)
if current.x == goal_node.x and current.y == goal_node.y:
print("Find goal")
goal_node.parent_index = current.parent_index
goal_node.cost = current.cost
break
''' Remove the item on open set '''
del open_set[c_id]
''' Add it to the closet set '''
closed_set[c_id] = current
''' expand search grid based on motion model'''
for move_x, move_y, move_cost in self.motion:
node = self.Node(current.x + move_x,
current.y + move_y,
current.cost + move_cost, c_id)
n_id = self.calc_index(node)
if n_id in closed_set:
continue
if not self.verify_node(node):
continue
if n_id not in open_set:
open_set[n_id] = node # Discover a new node
else:
if open_set[n_id].cost >= node.cost:
# This path is the best until now. record it!
open_set[n_id] = node
rx, ry = self.calc_final_path(goal_node, closed_set)
return rx, ry
def calc_final_path(self, goal_node, closed_set):
# generate final course
rx, ry = [self.calc_position(goal_node.x, self.min_x)], [
self.calc_position(goal_node.y, self.min_y)]
parent_index = goal_node.parent_index
while parent_index != -1:
n = closed_set[parent_index]
rx.append(self.calc_position(n.x, self.min_x))
ry.append(self.calc_position(n.y, self.min_y))
parent_index = n.parent_index
return rx, ry
def calc_position(self, index, minp):
pos = index * self.resolution + minp
return pos
def calc_xy_index(self, position, minp):
return round((position - minp) / self.resolution)
def calc_index(self, node):
return (node.y - self.min_y) * self.x_width + (node.x - self.min_x)
def verify_node(self, node):
px = self.calc_position(node.x, self.min_x)
py = self.calc_position(node.y, self.min_y)
if px < self.min_x:
return False
if py < self.min_y:
return False
if px >= self.max_x:
return False
if py >= self.max_y:
return False
if self.obstacle_map[node.x][node.y]:
return False
return True
def calc_obstacle_map(self, ox, oy):
self.min_x = round(min(ox))
self.min_y = round(min(oy))
self.max_x = round(max(ox))
self.max_y = round(max(oy))
print("min_x:", self.min_x)
print("min_y:", self.min_y)
print("max_x:", self.max_x)
print("max_y:", self.max_y)
self.x_width = round((self.max_x - self.min_x) / self.resolution)
self.y_width = round((self.max_y - self.min_y) / self.resolution)
print("x_width:", self.x_width)
print("y_width:", self.y_width)
# obstacle map generation
self.obstacle_map = []
''' Iterate over the x, y indices '''
for _ in range(self.x_width):
row = []
for _ in range(self.y_width):
row.append(False)
self.obstacle_map.append(row)
''' Iterate over x indices '''
for ix in range(self.x_width):
x = self.calc_position(ix, self.min_x)
for iy in range(self.y_width):
y = self.calc_position(iy, self.min_y)
''' Iterate over obstacles' x and y coordinates '''
for iox, ioy in zip(ox, oy):
''' Calculate Euclidean distance between obstacle and current point '''
d = math.hypot(iox - x, ioy - y)
if d <= self.robot_radius:
self.obstacle_map[ix][iy] = True
break
@staticmethod
def get_motion_model():
''' motion model for obstacle '''
motion = [[1, 0, 1],
[0, 1, 1],
[-1, 0, 1],
[0, -1, 1],
[-1, -1, math.sqrt(2)],
[-1, 1, math.sqrt(2)],
[1, -1, math.sqrt(2)],
[1, 1, math.sqrt(2)]]
return motion
def main():
print(__file__ + " start!!")
# start and goal position
sx = 10.0 # [m]
sy = 10.0 # [m]
gx = 50.0 # [m]
gy = 50.0 # [m]
grid_size = 2.0 # [m]
robot_radius = 1.0 # [m]
# set obstacle positions
ox, oy = [], []
for i in range(60):
ox.append(i)
oy.append(0.0)
for i in range(60):
ox.append(60.0)
oy.append(i)
for i in range(61):
ox.append(i)
oy.append(60.0)
for i in range(61):
ox.append(0.0)
oy.append(i)
for i in range(40):
ox.append(20.0)
oy.append(i)
for i in range(0, 40):
ox.append(40.0)
oy.append(60.0 - i)
if show_animation = True # pragma: no cover
plt.plot(ox, oy, ".k")
plt.plot(sx, sy, "og")
plt.plot(gx, gy, "xb")
plt.grid(True)
plt.axis("equal")
plt.show()
else:
show_animation = False
dijkstra = Dijkstra(ox, oy, grid_size, robot_radius)
rx, ry = dijkstra.planning(sx, sy, gx, gy)
if show_animation = True # pragma: no cover
plt.plot(rx, ry, "-r")
plt.grid(True)
plt.pause(0.01)
plt.show()
else:
show_animation = False
if __name__ == '__main__':
main()
Djikstra算法结果
Dijkstra算法优点
- 最佳解决方案:Dijkstra 算法保证找到起始节点和图中所有其他节点之间的最短路径,前提是该图具有非负边权重。这种最优性确保机器人采用最有效的路线到达目的地。
- 完整性:Dijkstra 算法是完整的,这意味着如果存在解决方案,它总是会找到解决方案。如果从起始节点到目标节点存在有效路径,Dijkstra 算法就会发现它。
- 可扩展性:Dijkstra 算法在具有适度数量的节点和边的图上表现良好。其时间复杂度为O((V + E) log V),其中V是节点数,E是边数。这使得它适用于许多现实世界的路径规划场景。
- 灵活性:Dijkstra 算法可以应用于各种图表示,包括有向图和无向图。它还可以处理加权图,其中不同的边具有不同的成本或距离
- 增量更新:Dijkstra 算法允许对图进行增量更新。如果环境发生变化或出现新的障碍物,算法可以重新运行以找到更新的最短路径,而无需从头开始。
- 广泛的适用性:Dijkstra 的算法广泛应用于各种应用,包括机器人、导航系统、网络路由和物流。其多功能性和经过验证的有效性使其成为自主机器人路径规划的热门选择