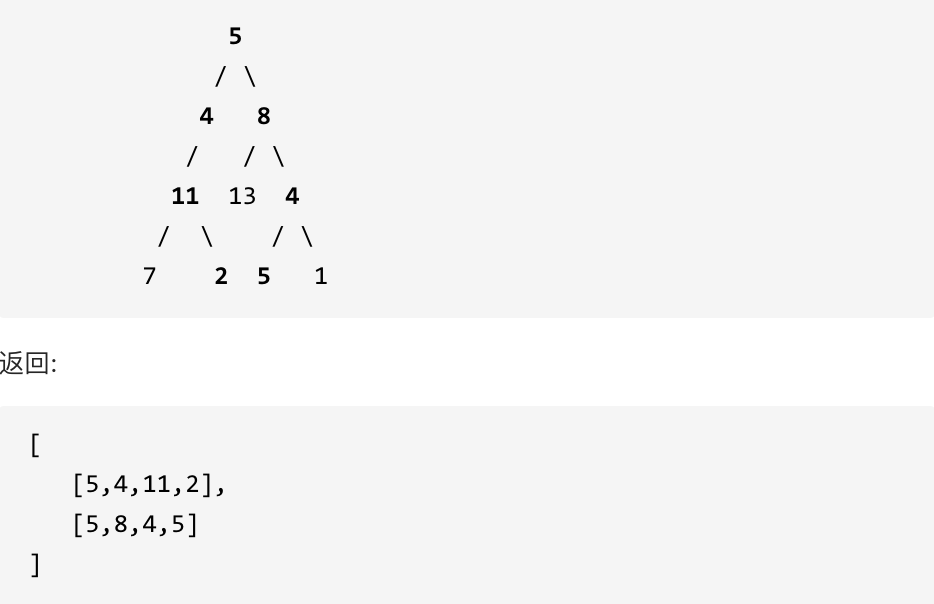
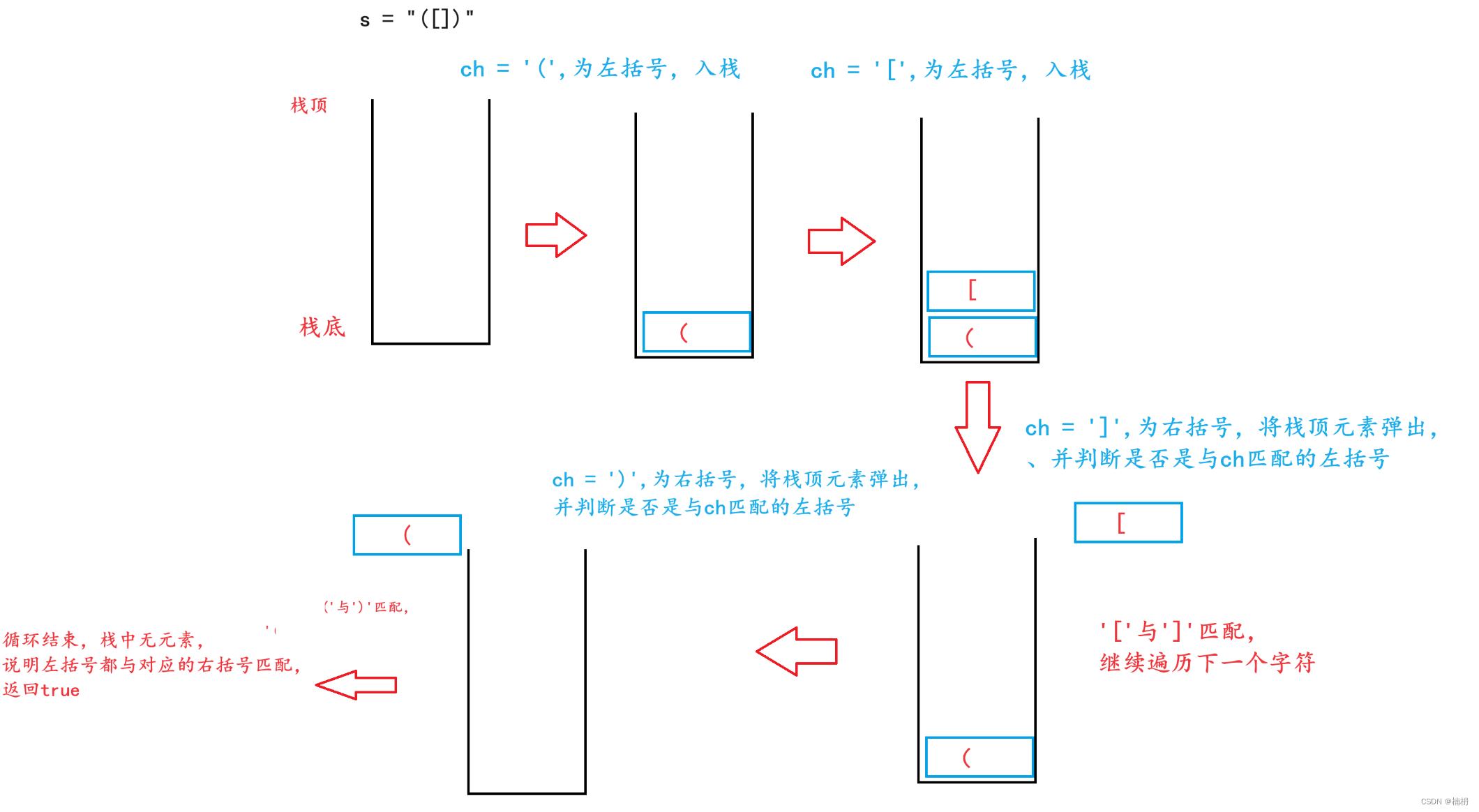
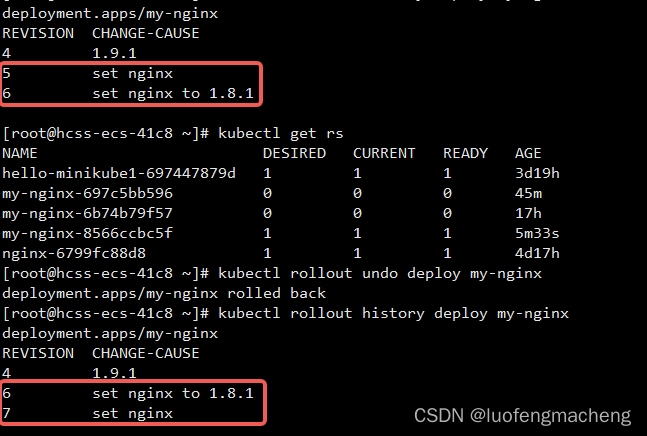
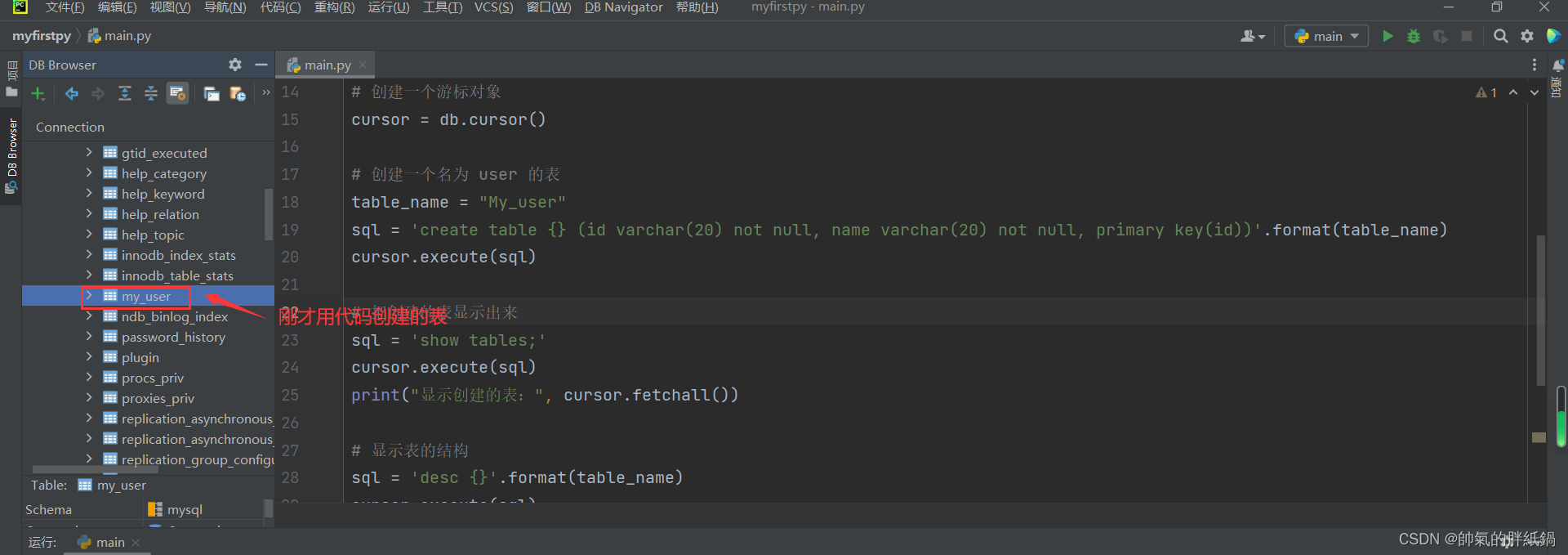
小小演示一下:
大体思路:
其实很早就想写一个俄罗斯方块了,但是一想到那么多方块还要变形,还要判断落地什么的就脑壳疼。直到现在才写出来。
俄罗斯方块这个小游戏的小难点其实就一个,就是方块的变形,看似每个方块的变形都不一样,找不到共同点,实现起来比较麻烦,不过只要有了思路其实还是可以的。
方块变形:
俄罗斯方块实际上是只有五种(其中有两种“L”形和“Z”形每种有两种对称的)。
每个方块以及变形的样子我都放下面了。


咋一看好像看不出共同点,不过也确实没有啥共同点,实际上我们不需要有共同点,我们只需要知道每个方块变形都是怎么变的。
上面看不出来我们再换个形式。

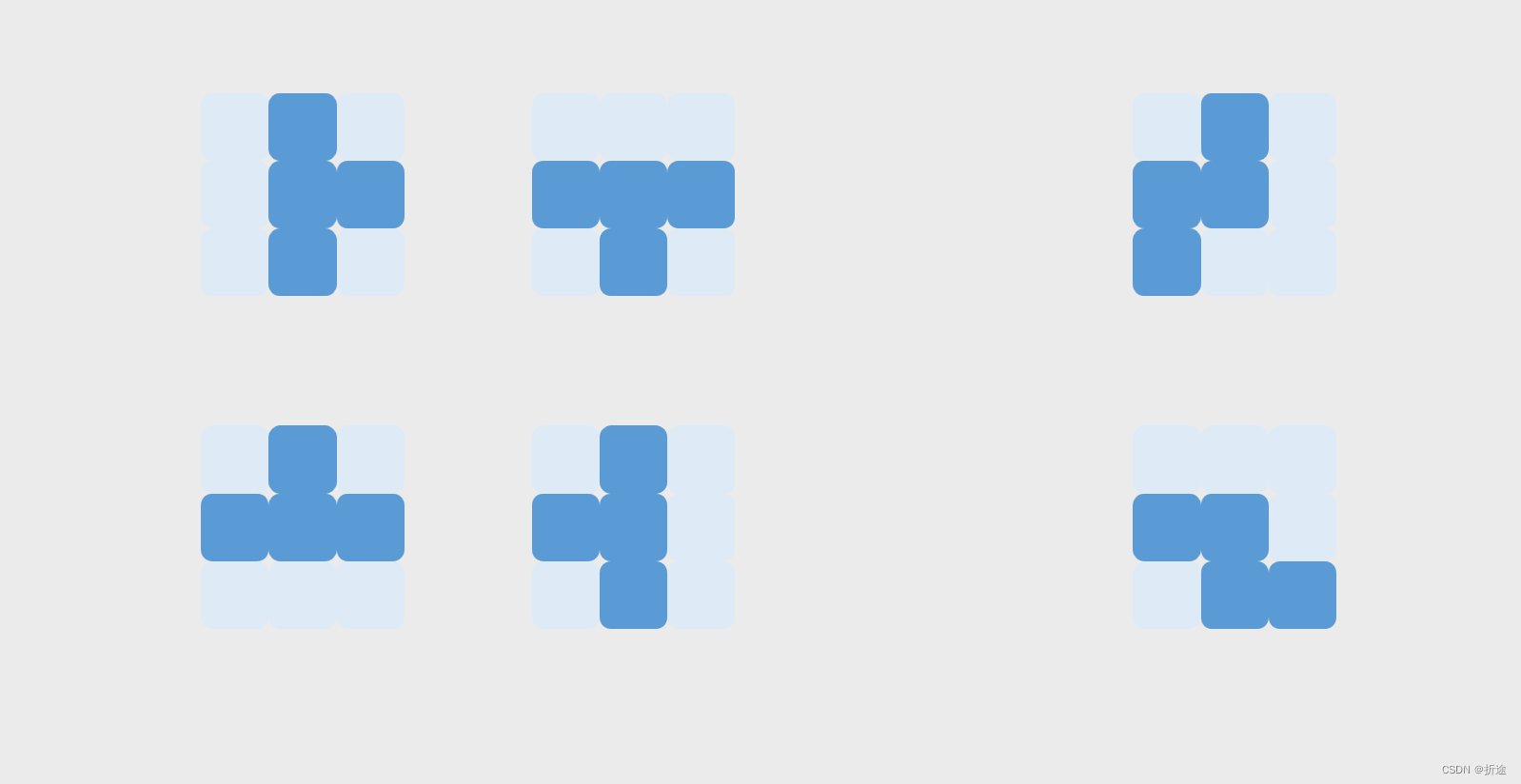
我们知道,方块变形的本质实际上是旋转,而旋转我们是绕着某个中心点去旋转的,因此我们只需要记录每个方块的中心点以及不同形态时的每个小方块对于中心点的相对位置。
除了正方形怎么变形都一样,其他方块的变形情况都在下面,中心点我加重了颜色。
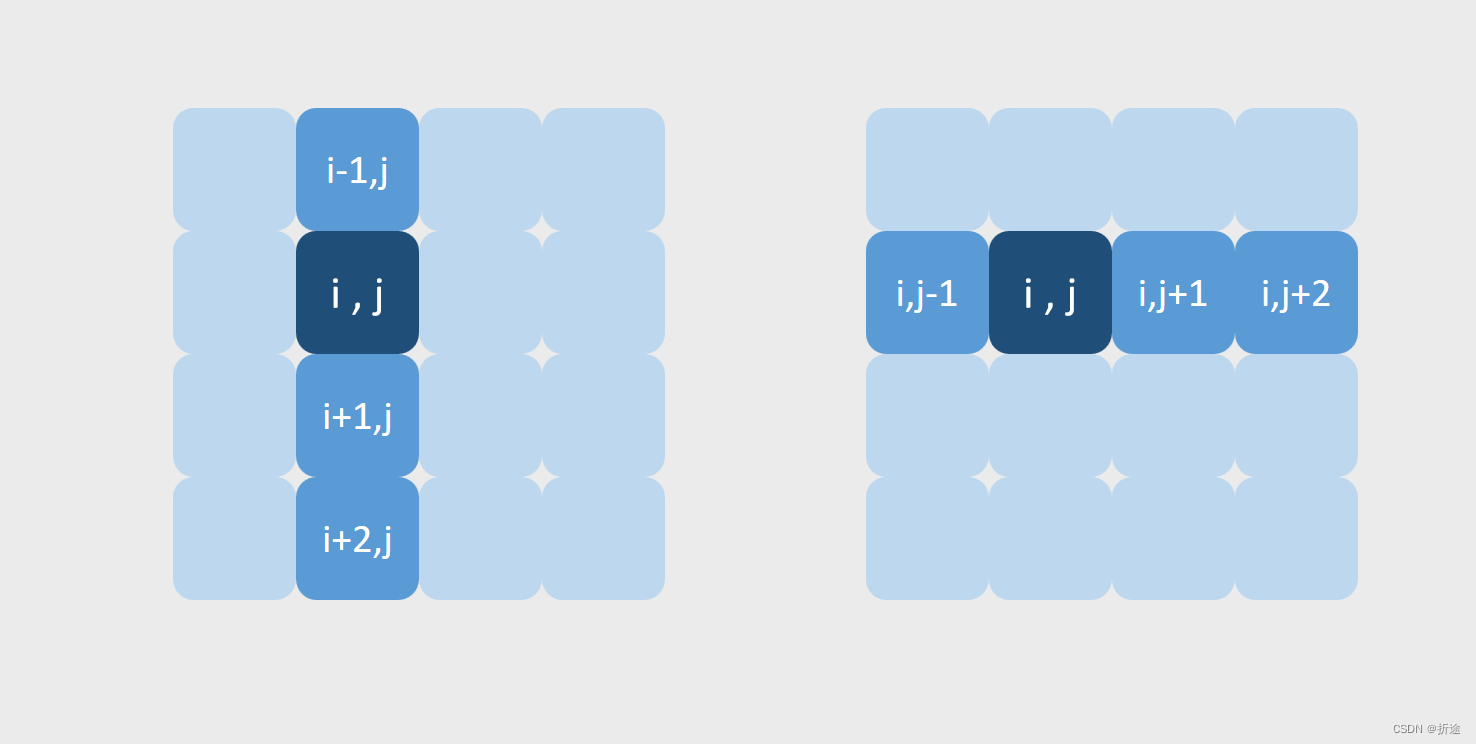
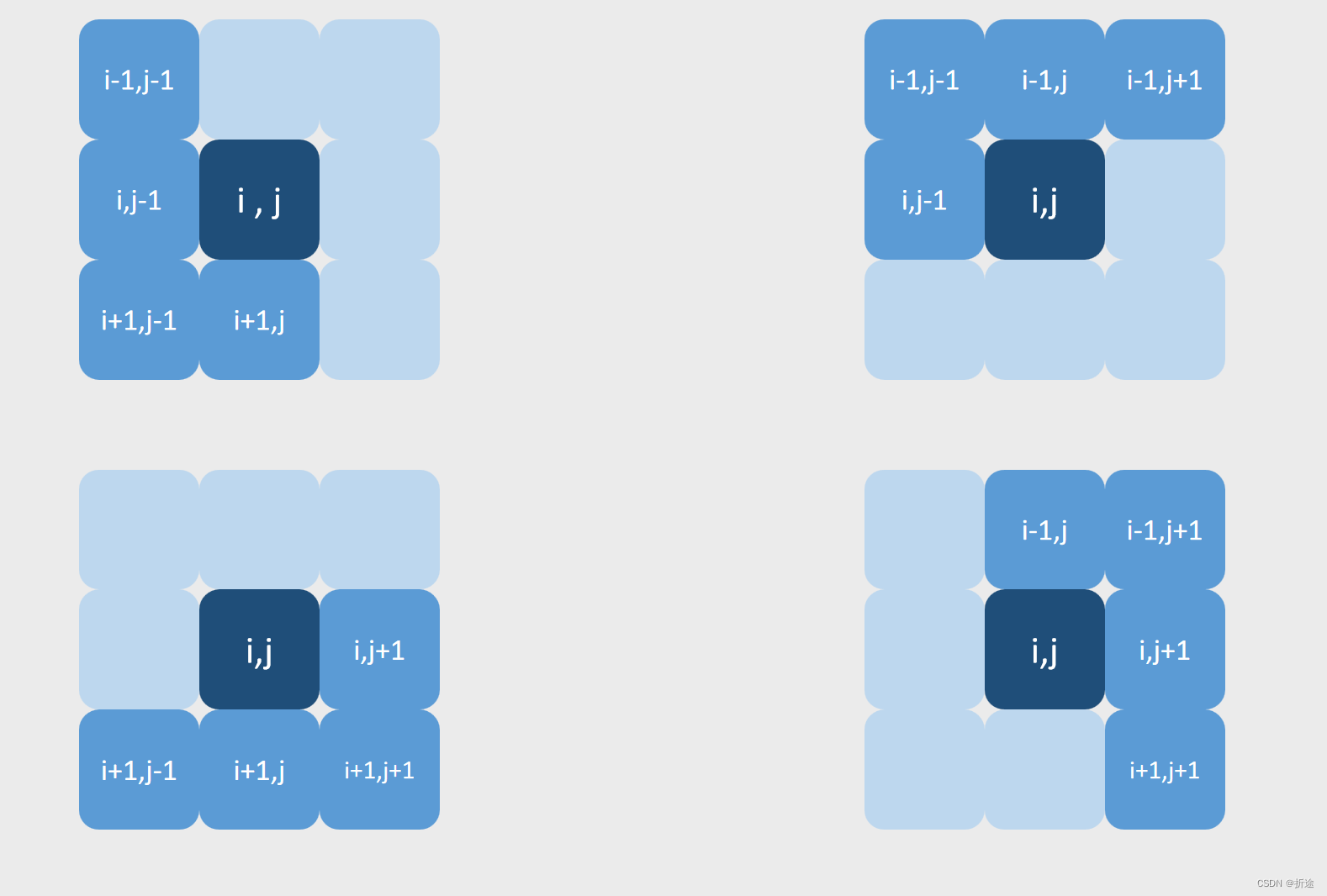
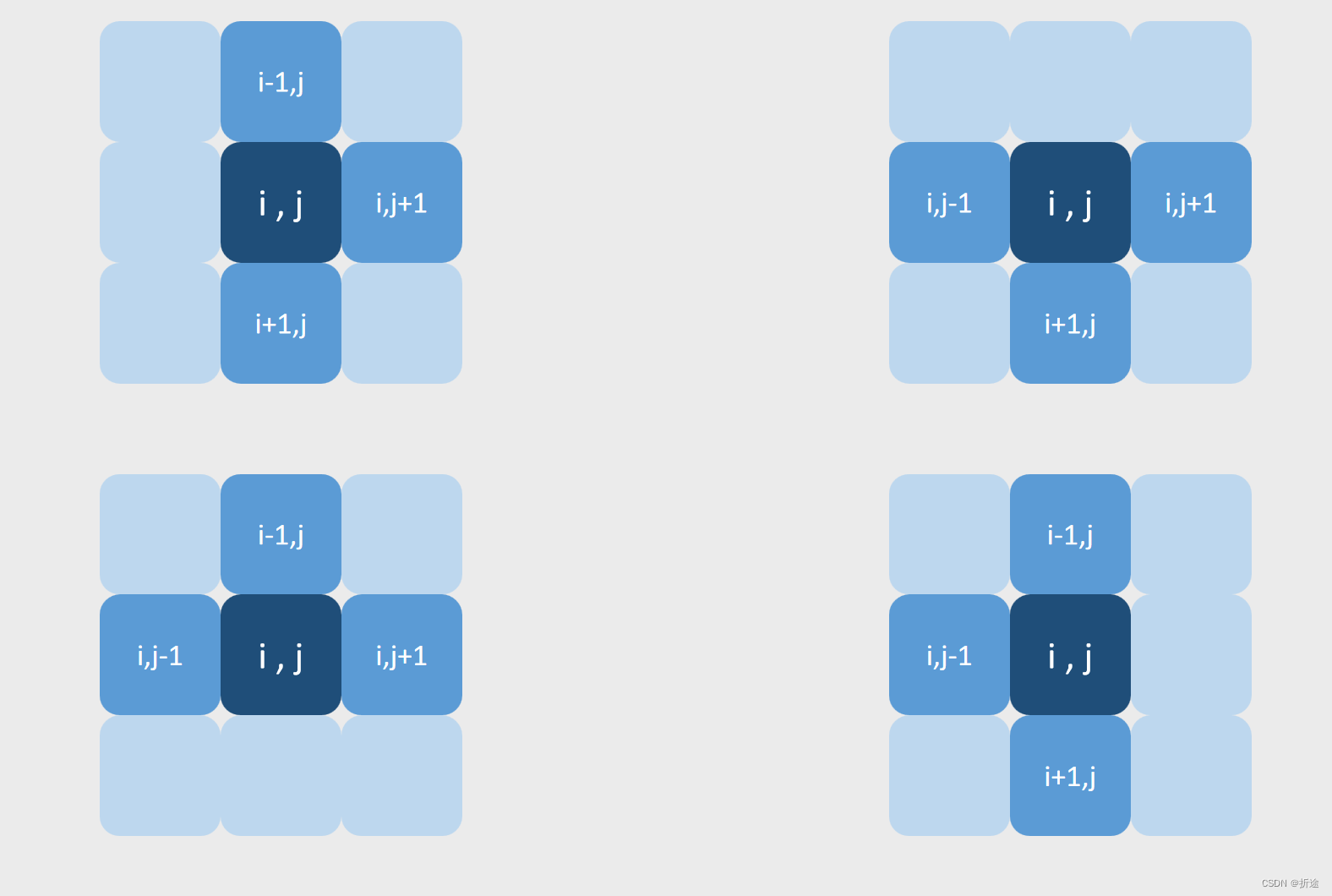
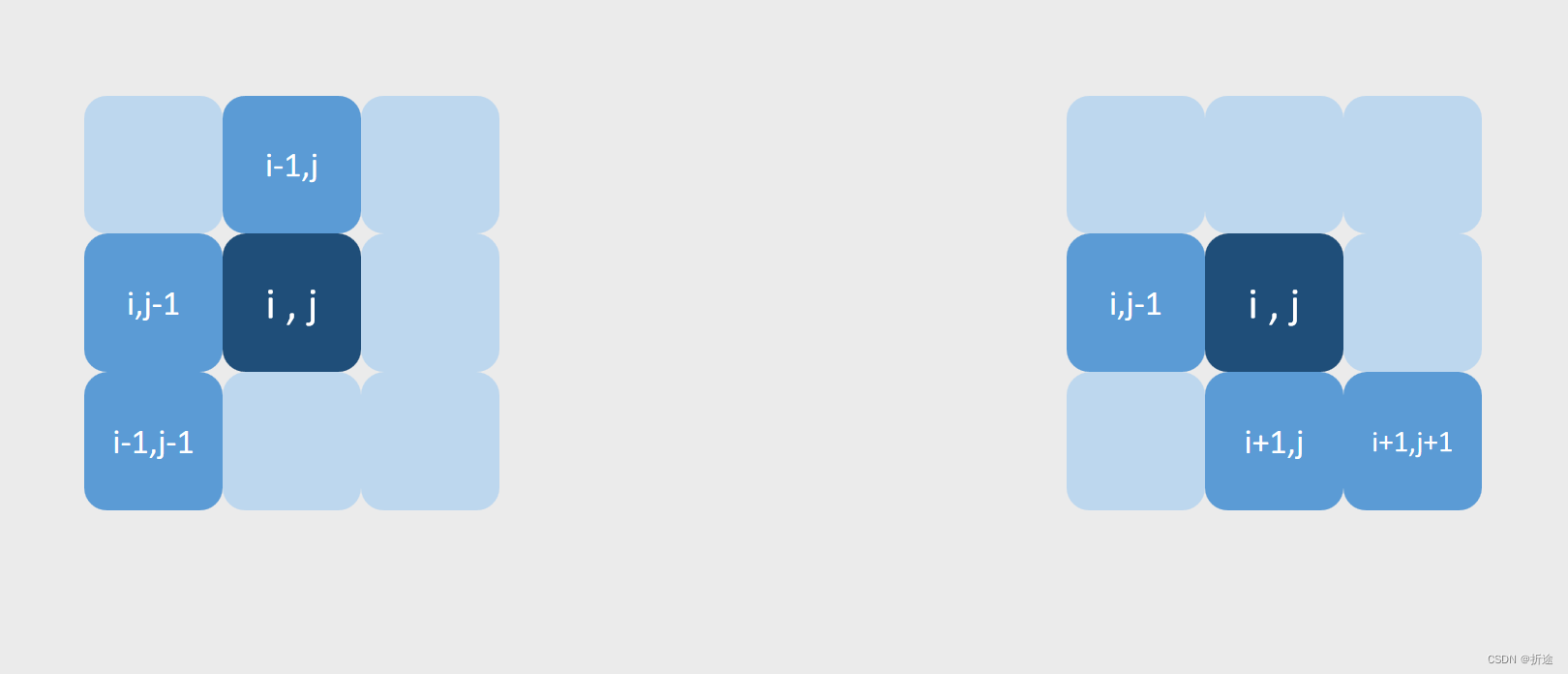
可以看得出来,方块的每个小方块的位置都可以通过与中心点的相对坐标来获取。
要变换姿势的时候,只要有中心点的坐标,就可以切换姿势。
下面是不同方块不同姿势的不同小方块与中心点的相对位置关系,套了个四维数组写起来好费劲:
//第一层选择方块种类,第二层选择方块形态,第三层装小方块,
//第四层装每个小方块对于中心点坐标的相对位置用于变换姿势
vector<vector<vector<vector<int>>>>mode{
{{{1,0},{1,1},{0,0},{0,1}}}, //方形
{{{2,0},{1,0},{0,0},{-1,0}},{{0,-1},{0,0},{0,1},{0,2}}}, //长条形
{{{1,0},{1,-1},{0,-1},{-1,-1}},{{1,-1},{1,0},{1,1},{0,1}}, //L形1
{{1,1},{0,1},{-1,1},{-1,0}},{{0,-1},{-1,-1},{-1,0},{-1,1}}},
{{{1,0},{1,1},{0,1},{-1,1}},{{1,-1},{1,1},{1,0},{0,-1}}, //L形2
{{0,1},{-1,0},{-1,1},{-1,-1}},{{1,-1},{0,-1},{-1,-1},{-1,0}}},
{{{1,0},{0,0},{0,1},{-1,0}},{{0,-1},{0,0},{0,1},{-1,0}}, //凸形
{{1,0},{0,0},{0,-1},{-1,0}},{{1,0},{0,0},{0,-1},{0,1}}},
{{{1,-1},{0,-1},{0,0},{-1,0}},{{1,0},{1,1},{0,0},{0,-1}}}, //Z形1
{{{1,1},{0,0},{0,1},{-1,0}},{{1,-1},{1,0},{0,0},{0,1}}} //Z形2
};下面是换姿势的代码:
其中 whichOne是选择哪一种方块,index是选择方块的哪一种姿势
//切换模式
vector<vector<int>> block::changeMode(){
if (whichOne == 0) return coordinate;
vector<vector<int>>res;
index++;
index %= (mode[whichOne].size());
for (auto& m : mode[whichOne][index]) {
//根据中心坐标和缓存的模式关系来获取切换模式之后的方块坐标
res.push_back({ center[0] - m[0],center[1] - m[1] });
}
//没有直接切换,而是返回新坐标
return res;
}在获取新姿势的小方块坐标之后没有马上更新,而是返回出去了,因为可能变形之后会不符合要求,例如下面的例子:
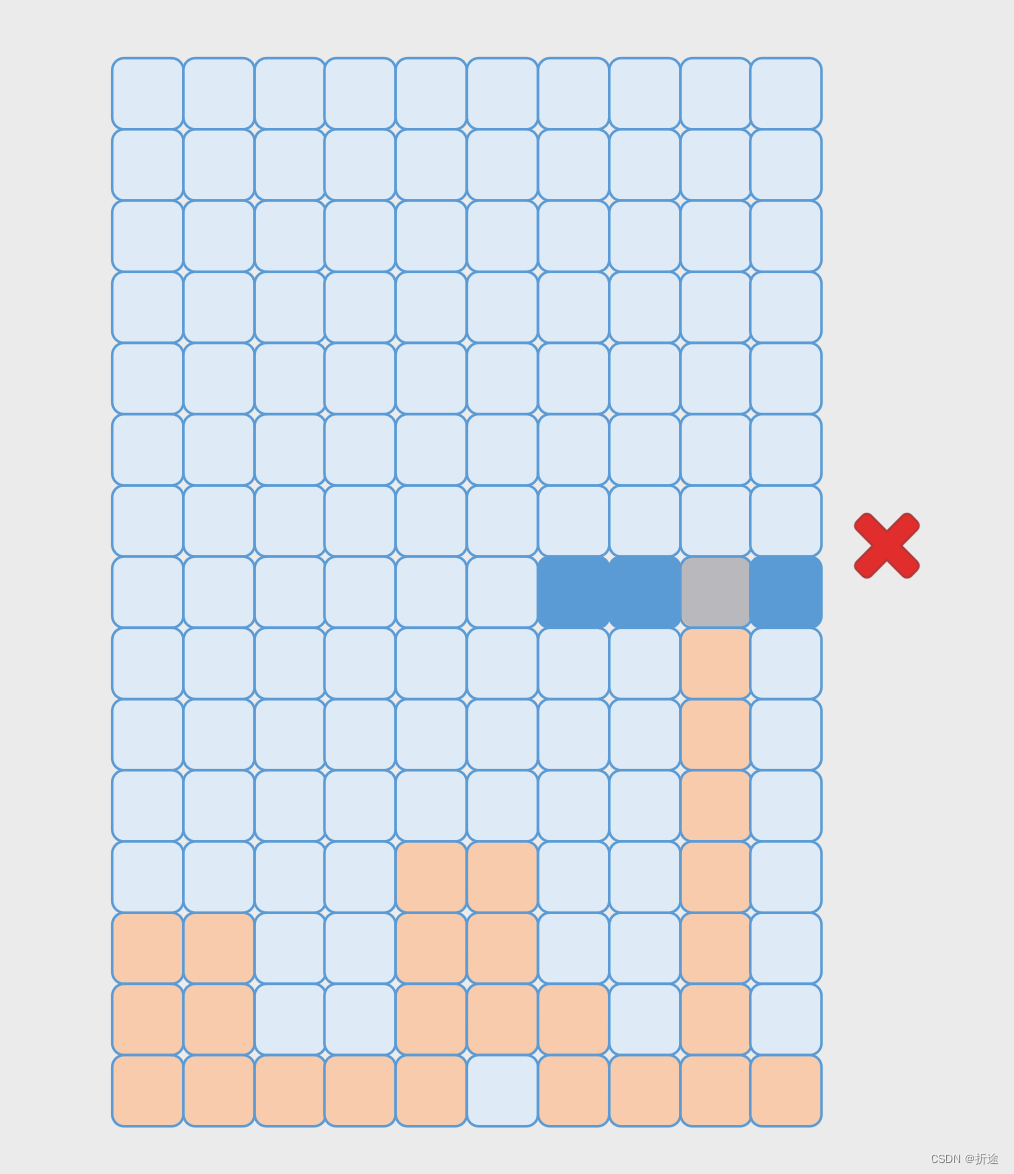
变形之后把返回的新坐标返回,我们再用一个函数去检测新坐标是否合法,合法再去修改当前方块的具体坐标,检测函数也很简单:
//检测移动是否合法
int Tetris::checkMove(vector<vector<int>>temp){
for (auto& c : temp) {
if (c[1] < 0 || c[1] >= 10) return -1; //左右越界返回-1;
if (cache[c[0]][c[1]] == 1) return 0; //遇到落地方块返回0;
}
//一切合法返回1
return 1;
}返回1就是移动合法,我们修改坐标,返回-1就是移动不合法,我们什么也不改。
还剩一个返回-1,就是移动后遇到了已经落地的方块,这时候在调用这个检测函数的函数之中还需要做个判断。
如果是因此下落而造成的移动,那么检测获取-1则将方块的坐标的位置更新对应在缓存中的位置为1,然后生成新方块。
而其他情况,例如是左右移动或是变换姿势而造成的碰到落地方块则是和-1一样不做处理。
否则会有这样的问题:

落地判断:
用Qt来绘图,我向来都是用二维数组来缓存界面,然后通过相应的位置的不同元素来绘制不同的图案。
在这个俄罗斯方块中,我的写法是缓存中的元素一共只有两种情况,0和1,0表示什么都没有,不需要绘制,而1表示已经落地的方块。
那么正在下落的方块呢,缓存里不用存一下吗。我的做法是不需要,等等会说明原因。
因此我们正在下落的方块的坐标我是拿另一个二维数组存起来的。
每次下落时只需要做个判断,我们正在下落的方块之中,只要有一个小方块在下落之后在缓存中对应的位置元素为1,就表示接触到了已经落地的方块,那么当前方块也会变成他们的一部分,然后更新缓存,并且重新生成新的方块。


这里有个小问题,就是在游戏的一开始缓存是全为0的,还没有落地的方块,因此我们上述的判断在游戏的一开始不会触发,解法有两种,一种是多一层判断,如果方块最下面的小方块已经到了界面最下面的地方(对应缓存中的下标为0),那么也算落地。
第二种解法是我的做法,就是直接在缓存下标为0的位置先给铺一层落地的方块也就是1。
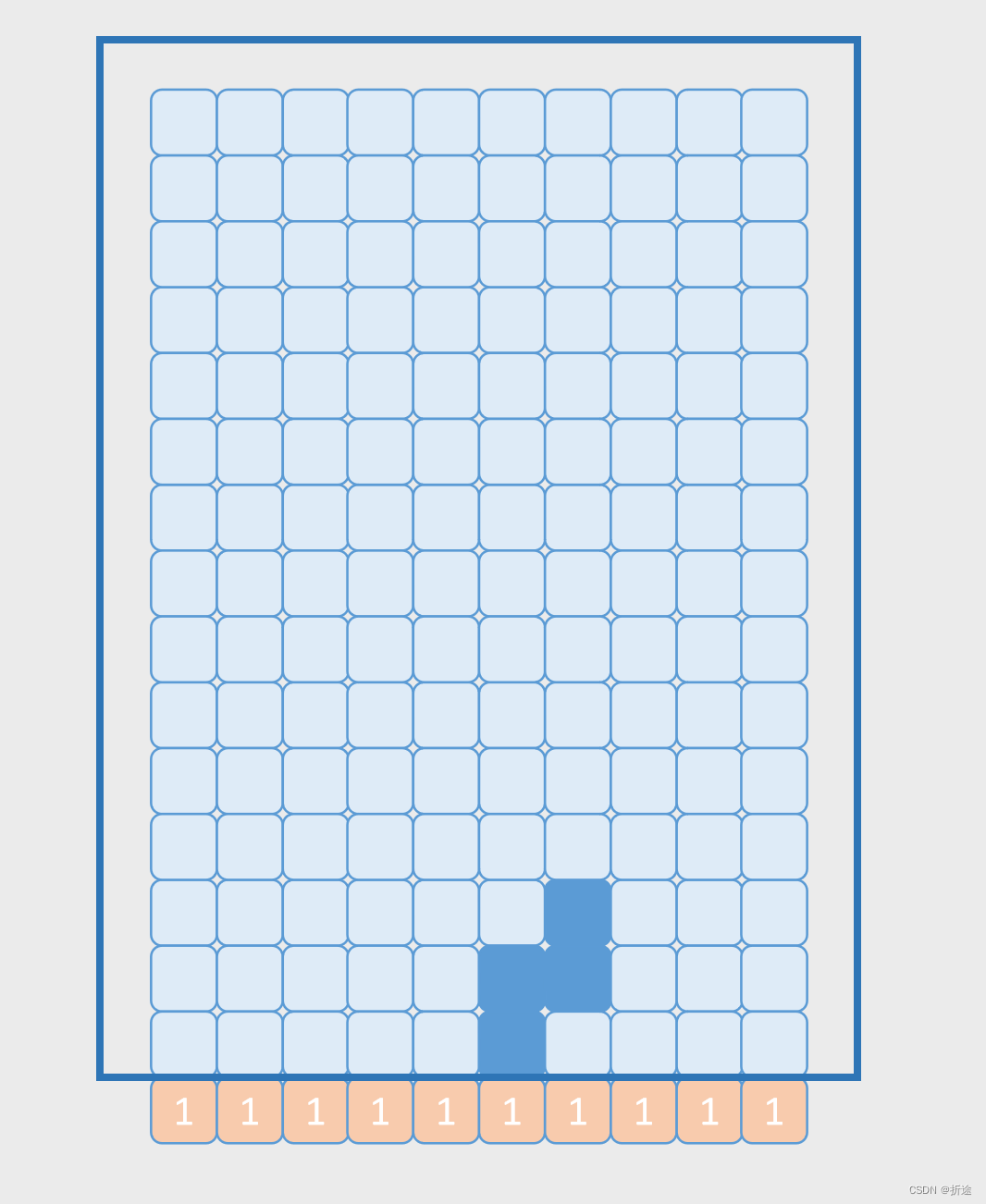
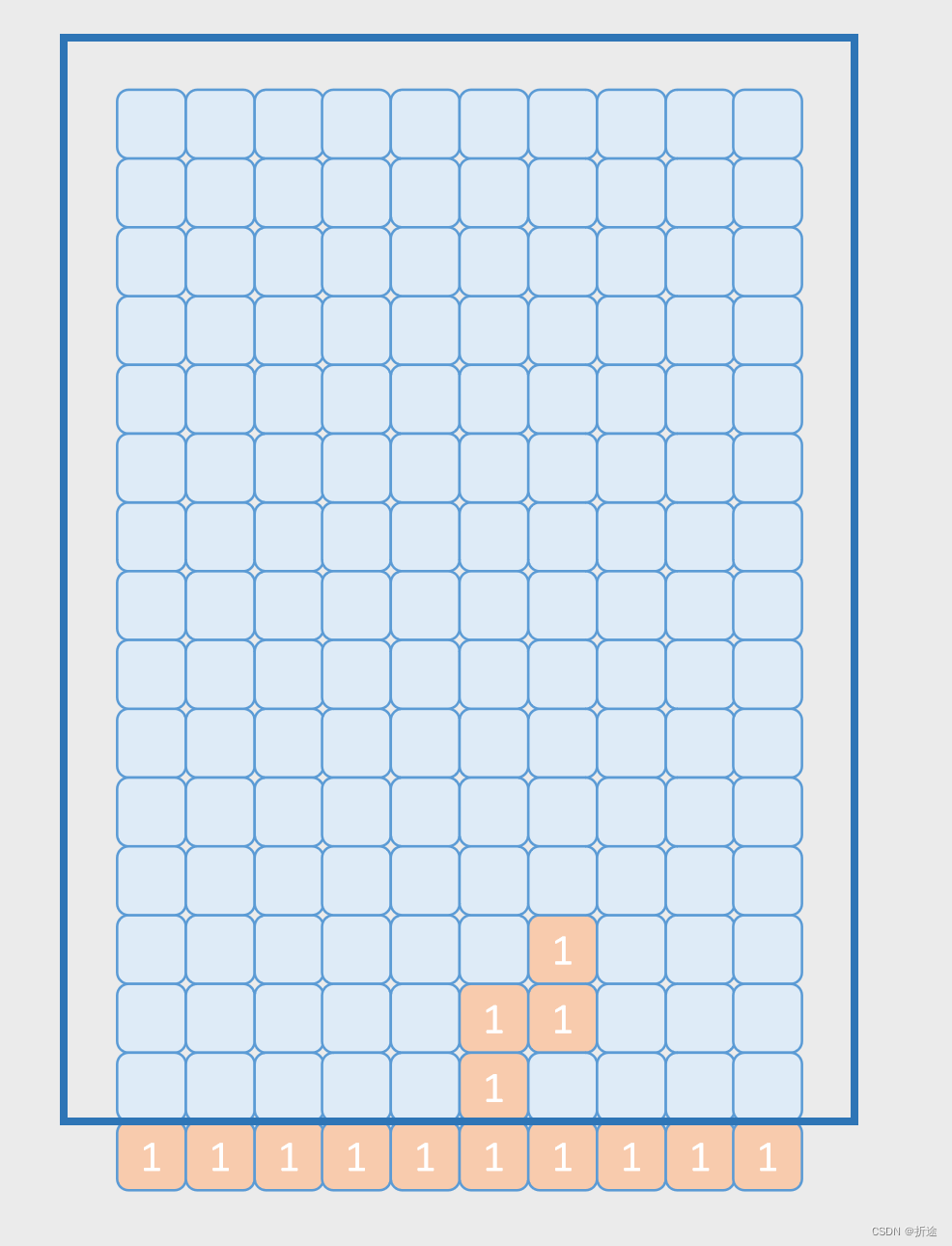
消除检测:
消除检测很容易,界面缓存中的元素只有0或1,分别用来表示什么都没有以及已经落地的方块,如果缓存中有一行的元素之和等于10,那么就表示本行塞满了,可以消除。
缓存中下标为0的行在最下面,也就是下标越大,代表的位置就在界面的越上方。
如果检测到了某一行可以消除,那么我们可以直接把这一行从缓存之中直接删除,然后从缓存的尾部再添加上一个长度为10,元素为0的数组即可。
关于消除还有最后一个问题,那就是一个方块落下,可能消除的不止一行,因此我们像上述那样操作,应该从下标较大的地方开始往下标较小的地方遍历寻找,否则可能会漏掉。
并且我们可以想象的到,一个方块落地之后,如果可以消除,那么可以消除的那一行方块一定是在刚落地方块所在的行,因此每次检测的时候,我们只需要检测落地方块的每个小方块所在的行即可。
//检测是否能清除一行方块
void Tetris::clearBlocks(){
set<int>s;
vector<int>v;
//获取方块的y轴,因为能清除方块的话,行数一定在方块的y轴之中
for (auto& c : curBlock.coordinate) {
if (accumulate(cache[c[0]].begin(), cache[c[0]].end(), 0) == 10) s.insert(c[0]);
}
//从大到小去清除一整行的界面缓存
for (int i : s) v.insert(v.begin(), i);
for (int i : v) {
score++; //得分增加
//删除一行方块后再后面补上一行.
cache.erase(cache.begin() + i);
cache.push_back(vector<int>(10, 0));
}
}
代码获取:
完整的项目文件我已经上传到了CSDN,可以直接免费下载,也可以关注我的公众号“折途想要敲代码”回复关键词“qt俄罗斯方块”免费获取、