【算法】递归（高阶题目） -随时补充

文章目录

岛问题
汉诺塔问题
牛群繁衍数量问题
求字符串的全部子序列
字符串的全排列
数字的全排列I
数字的全排列II
N皇后II
N皇后I

岛问题

递归的方法:

遍历岛这个二维数组，如果当前数为1，则进入感染函数并将岛个数+1
感染函数：其实就是一个递归标注的过程，它会将所有相连的1都标注成2 (去上下左右递归感染，直到把相连的一片1都感染)
- 为什么要标注？这样就避免了遍历过程中的重复计数的情况，一个岛所有的1都变成了2后，遍历的时候就不会重复遍历了，当然也可以选择标注为其他值！

class Solution {
public:
    //感染函数:从(i,j)位置出发,把所有连成一片的'1',变成'2'
    //因为要对grid数组修改,以及为了减少拷贝,要传引用
    void infect(vector<vector<char>>& grid,int i ,int j)
    {
        //保证i和j范围的合法性  并且如果 当前位置不是'1'就返回
        if(i<0 || i == grid.size() || j<0 || j == grid[0].size() || grid[i][j] != '1')
        {
            return ;
        }
        //把当前位置感染为'2'
        grid[i][j] = '2';
        //去该位置的上下左右感染
        infect(grid,i-1,j);//左
        infect(grid,i+1,j);//右
        infect(grid,i,j+1);//下
        infect(grid,i,j-1);//上
    }
    int numIslands(vector<vector<char>>& grid) {
        int island = 0;
        //遍历二维数组
        for(int i = 0;i<grid.size();i++)
        {
            for(int j = 0;j<grid[0].size();j++)
            {
                //如果当前字符为1,岛的数量++,进入感染函数
                if(grid[i][j] == '1')
                {
                    island ++;//岛的数量++
                    infect(grid,i,j);//进入感染函数
                }
            }
        }    
        return island;//最后返回岛的数量
    }
};

时间复杂度分析:矩阵为m*n的规模，所以时间复杂度为:O(m*n)

汉诺塔问题

n个圆盘从下面开始按大小顺序摆放在A柱子上，规定：任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘，求最少的移动步骤

void move(char start, char end)
{
	printf("move:%c->%c\n", start, end);
}

//pos1:起始位置(A)    pos2:中转位置(B)    pos3:目标位置(C)  n:盘子数量 
void Hanoi(char pos1, char pos2, char pos3,int n)
{
	if (n == 1) //只有一个盘子,直接将盘子从起始位置移动到目标位置
	{
		move(pos1, pos3);
		return;
	}

	Hanoi(pos1, pos3, pos2, n - 1);//将A位置上的n-1个盘子经过C移动到B
	move(pos1, pos3); //将A位置上剩余的盘子经过B移动到C
	Hanoi(pos2, pos1, pos3, n - 1);//将B位置上的n-1个盘子通过A移动到C
}
int main()
{
	Hanoi('A', 'B', 'C', 3);
	return 0;
}

结论：假设有n个盘子，移动次数为： $2^n -1$

牛群繁衍数量问题

母牛每年生一只母牛，新出生的母牛三年后也可以每年生一只母牛，假设母牛不会死,最开始母牛是A（就一个牛），求N年后母牛数量

方法：列出前几项找规律即可

$F (n)$ ：第 $n$ 年的母牛数量，$F(n) = F(n-1) + F(n-3) $ ：第N年的牛 = 前一年的牛 + 前三年的牛（三年前的牛现在就可以生）

int numOfCows(int n) 
{
    if(n<4)	return n;
    else return numOfCows(n - 1) + numOfCows(n - 3);
}

求字符串的全部子序列

子序列：在字符串当中任意的选取字符，可以不连续选取，最后形成的字符串称为子序列

//求字符串的子序列
void process(string str, int index, string path,vector<string>& ans)
{
	if (index == str.size())
	{
		ans.push_back(path);
		return;
	}
	process(str, index + 1, path + str[index], ans);//要当前index位置的字符,然后去index+1位置做选择
	process(str, index + 1, path, ans); //不要当前index位置的字符,去index+1位置做选择
}
//空串也算一种子序列=>全部字符都不要

如果要进行去重，那么可以把形成的子序列放到unordered_set当中

字符串的全排列

https://leetcode.cn/problems/zi-fu-chuan-de-pai-lie-lcof/)

全排列：字符串当中的所有字符都得选取，只能决定每个字符的顺序不一样

定义一个递归函数: $p rocess (原始字符串, 当前形成的字符串排列, 记录字符是否被使用过, 保存生成的字符串排列)$

为了方便进行去重，所以保存结果的结果集采用的数据结果是unordered_set

代码思路：

如果当前形成的字符串排列和原始字符串的长度一样：表示已经生成了一个结果，将其放到结果集当中保存
否则：遍历原始字符串当中的所有字符做选择，如果当前字符没有被选择过，那么就选中该字符，生成下一个字符，最后要记得进行回溯！

class Solution {
public:
    void process(string& str,string path,vector<bool>& visited,unordered_set<string>& ans)
    {
        if(path.size() == str.size()) 
        {
            ans.insert(path);
            return ;
        }
        int n = str.size();
        for(int i = 0;i<n;i++)//遍历原始字符串中的所有字符进行选择
        {
            if(!visited[i]) //当前i位置的字符没有被选择过
            {
                visited[i] = true;// 标记该字符已经被选中
                process(str,path+str[i],visited,ans); // 继续生成下一个字符
                visited[i] = false; // 取消该字符的标记,恢复现场
            }
        }
    }
    vector<string> permutation(string s) {
        vector<bool> visited(256,false);//字符是否有被选取
        unordered_set<string> ans;
        string tmp;
        process(s,tmp,visited,ans);
        return vector<string>(ans.begin(),ans.end());
    }
};

数字的全排列I

https://leetcode.cn/problems/permutations/description/

给定一个不含重复数字的数组 nums ，返回其所有可能的全排列。你可以 按任意顺序 返回答案

和上述字符串的全排列基本一致！

1 <= nums.length <= 6，所以此时的记录数组只需要开辟7个空间即可标志每个位置的字符是否被选择

class Solution {
public:
    void process(vector<int>& nums,vector<int> path,vector<bool>& visited,vector<vector<int>>& ans)
    {
        if(path.size() == nums.size())
        {
            ans.push_back(path);
            return ;
        }
        int n = nums.size();
        for(int i = 0;i<n;i++)
        {
            if(!visited[i])
            {
                visited[i] = true;
                path.push_back(nums[i]);
                process(nums,path,visited,ans);
                visited[i] = false;
                path.pop_back(); //此处回溯的时候记得要在path当中弹出元素！！！
            }
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        vector<bool> visited(7,false);//i位置的字符是否被选择
        vector<vector<int>> ans;
        vector<int> v;
        process(nums,v,visited,ans);
        return ans;
    }
};

数字的全排列II

https://leetcode.cn/problems/permutations-ii/description/

给定一个可包含重复数字的序列 nums ，按任意顺序返回所有不重复的全排列

做法：关键是去重！除重思路：先对nums数组进行sort，使得相同的数字都排在一起。

思想：如果当前 $i$ 位置被使用过或者当前位置的元素和前一个位置的元素相同 && 前面一个元素没有被使用过 =>就不能选择当前位置的元素

if(visited[i] || (i>0 &&  nums[i] == nums[i-1] && !visited[i-1])) //去重
            continue;

class Solution {
public:
    void process(vector<int>& nums,vector<int> path,vector<bool>& visited,vector<vector<int>>& ans)
    {
        if(path.size() == nums.size())
        {
            ans.push_back(path);
            return ;
        }
        int n = nums.size();
        for(int i = 0;i<n;i++)
        { 
          if(visited[i] || (i>0 &&  nums[i] == nums[i-1] && !visited[i-1])) //去重
            continue;
          else 
          {
                visited[i] = true;
                path.push_back(nums[i]);
                process(nums,path,visited,ans);
                visited[i] = false;
                path.pop_back();
          }
        }
    }
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        vector<bool> visited(256,false);//字符是否有被选取
        vector<vector<int>> ans;
        vector<int> v;
        sort(nums.begin(),nums.end()); //先排序！！！！
        process(nums,v,visited,ans);
        return ans;
    }
};

N皇后II

https://leetcode.cn/problems/n-queens-ii/description/

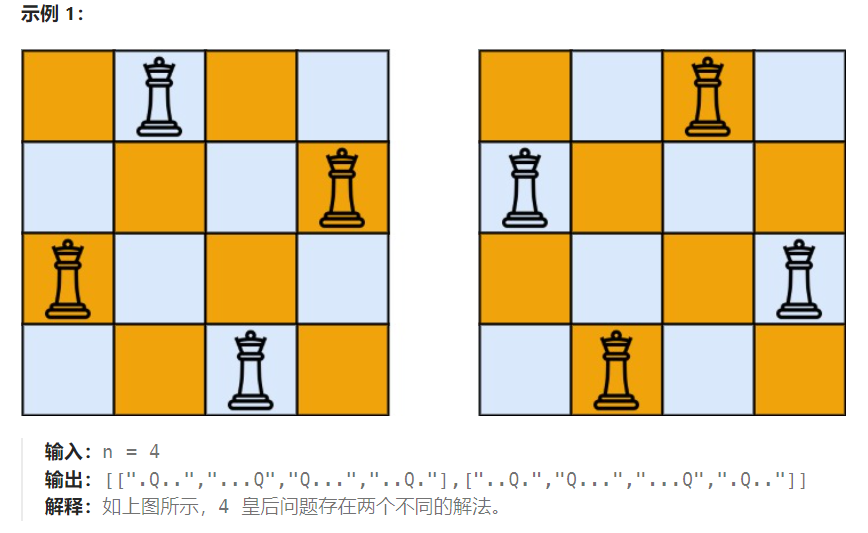
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量

即：任何两个皇后不同行、不同列、也不在同一条斜线上

做法：

1.使用一个轨迹数组：保存每一行皇后存放的位置，每一行只填一个皇后就解决了皇后不同行的问题！只需再保证不同列和不在一条斜线

$recor d [i] = x$ ：第 $i$ 行的皇后放在第 $x$ 列。有多少个皇后，轨迹数组就开辟多大

2.假设之前的某个皇后放在了 $x 行 y 列,$ 此时的皇后假设放在 $甲行乙列$ ，如果：y == 乙 (共列) || 甲-x的绝对值==乙-y的绝对值 (共斜线 => 坐标行相减的绝对值 == 坐标列相减的绝对值)，那么此时这两个皇后就是打架的！

//判断现在i行的皇后如果放在j列上,和之前的皇后是否不打架
bool isValid(vector<int>& record, int i, int j)
{
	// 检查0~i-1行的皇后和此时放置在i行j列的皇后是否打架！
	for (int k = 0; k < i; k++)
	{
		//第k行的皇后 record[k]:第k行的皇后放在哪一列
		//共列 || 共斜线(坐标行相减的绝对值 == 坐标列相减的绝对值) -> 就打架
		if (j == record[k] ||abs(record[k] - j) == abs(i - k)) 
		{
			return false;
		}
	}
	//不打架！ 当前第i行的皇后可以放在第j列！
	return true;
}

3.准备一个递归处理函数： $p rocess (in d e x, recor d, n)$ ：当前要在第 $in d e x$ 行放置皇后，之前的皇后的位置都记录在了 $recor d$ 轨迹数组当中，一共有 $n$ 行，返回后续有多少种放置方法

只需要在 $in d e x$ 行当中的所有列遍历一遍，尝试当前列是否可以放该皇后，保证跟之前所有的皇后不打架即可

int process(int index, vector<int>& record, int n)
{
    if (index == record.size())
    {
        //index到了终止位置:说明之前的皇后在不打架的情况下,所有的皇后填完了,那么之前做过的决定就是一种方法
        return 1;
    }
    int res = 0;
    //第index行的皇后放在哪一列呢?从第0列开始试一遍,只要和之前的皇后不打架就可以放！
    for (int cur = 0; cur < n; cur++)
    {
        //isValid:检查index行的皇后放在cur列是否会和之前的皇后打架
        if (isValid(record, index, cur))
        {
            //不打架,此时cur列可以放该皇后
            record[index] = cur;//当前皇后放在i行j列上

            res += process(index + 1, record, n);//统计当前皇后放在cur列,往后放皇后最后满足条件的方法数
        }
        //如果打架,就去考虑放在下一个位置
    }
    return res;
}
int totalNQueens(int n) {
    if (n < 1)
    {
        return 0;
    }
    vector<int> record(n);
    return process(0,record,n);
}

N皇后I

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案，'Q' 和 '.' 分别代表了皇后和空位。

记录有效的情况下的n皇后的摆放情况

针对上面的代码做修改：

在递归函数当中多增加一个参数：用于保存有效的情况下的n皇后的摆放情况，当index == n的时候，之前做过的决定就是一种有效方法，在这个位置处理n皇后的摆放情况
递归函数不需要返回方法数了，因为要的是摆放情况

//generateBoard:将当前n皇后的位置信息保存
void generateBoard(vector<int>& record,int n,vector<string>& res)
{
    //一行一行处理,先填满 '.' 再填皇后的列位置即record[index]为'Q'
    for(int index = 0;index<n;index++)
    {
        //ans:当前第index行的情况
        string ans(n,'.');//用n个;.'初始化ans
        ans[record[index]]='Q';//当前index行的皇后放在该行的record[index]列中
        res.push_back(ans);
    }
}
void process(int index, vector<int>& record, int n,vector<vector<string>>& result)
{
    if (index == record.size())
    {
        //index到了终止位置:说明之前的皇后在不打架的情况下,所有的皇后填完了
        //那么之前做过的决定就是一种有效方法
        vector<string> res;
        generateBoard(record,n,res);
        result.push_back(res);
    }
    //........................
}