原始 Markdown文档、Visio流程图、XMind思维导图见:https://github.com/LiZhengXiao99/Navigation-Learning
文章目录
- 三、因子图优化(FGO)
- 1、因子图模型
- 2、因子图优化状态估计模型
- 3、因子图优化求解
- 4、Ceres 非线性最小二乘库
- 5、GICI-LIB 中的图优化模型
- 1. 两种因子图结构
- 2. 边缘化 Marginalization
- 3. 关键帧 keyframes
- 4. 图优化类 Graph
- 5. 定位模式
- GNSS
- GNSS+ INS
- GNSS + INS + Camera
- Estimator 类型封装
- Estimator 类型封装
三、因子图优化(FGO)
1、因子图模型
因子图作为一种数学工具,是用因子描述多变量复杂函数的二维图,经常被用于多源融合导航中。因子图优化就是将优化问题转换成图的形式,图由边和顶点组成。边连接着顶点,表示顶点之间的一种关系。顶点表估计问题中的未知随机变量,而因子表示有关这些变量的概率信息,从测量或先验信息中可以得出。
因子图是一种二分图模型,它表征了全局函数和局部函数之间的关系,同时也表示了各个变量与局部函数之间的关系,以下式为例:
g
(
x
1
,
x
2
,
x
3
,
x
4
,
x
5
)
=
f
A
(
x
1
)
f
B
(
x
2
)
f
C
(
x
1
x
2
x
3
)
f
D
(
x
3
x
4
)
f
E
(
x
3
x
5
)
{\begin{array}{l} g\left(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right)=f_{A}\left(x_{1}\right) f_{B}\left(x_{2}\right) f_{C}\left(x_{1} x_{2} x_{3}\right) f_{D}\left(x_{3} x_{4}\right) f_{E}\left(x_{3} x_{5}\right) \end{array}}
g(x1,x2,x3,x4,x5)=fA(x1)fB(x2)fC(x1x2x3)fD(x3x4)fE(x3x5)
将全局函数
g
g
g 转化为局部函数
f
f
f 的乘积,其对应的因子图如下所示:
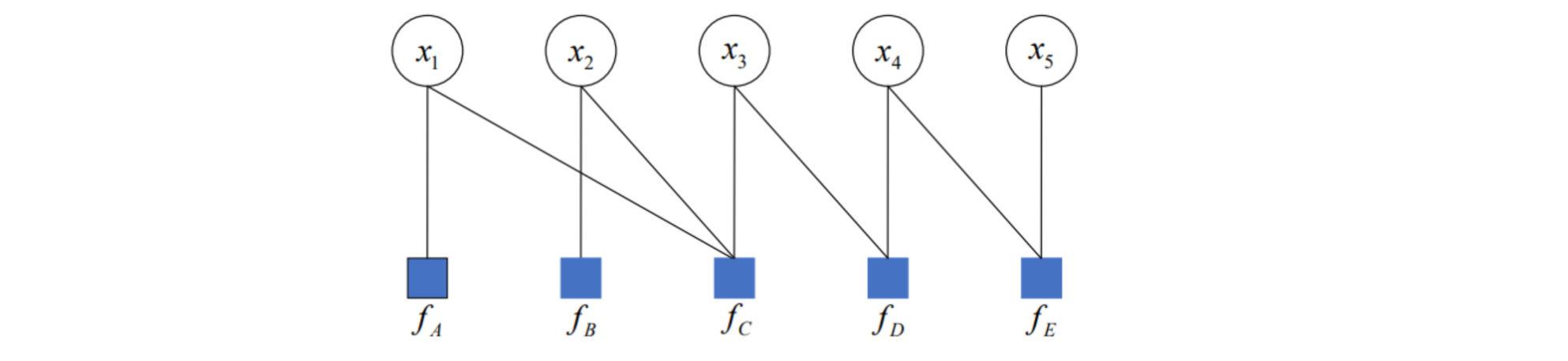
- 圆圈:每一个变量 x x x 对应一个变量结点。
- 正方形:每一个局部函数 f f f 对应一个因子结点。
- 线:当且仅当变量 x x x 是局部函数 f f f 的的自变量时,相应的变量节点和因子节点之间有一条边连接两个节点。
2、因子图优化状态估计模型
状态估计问题,就是是寻找
X
X
X 来最好地描述观测值
Z
Z
Z。根据贝叶斯法则,状态量
X
X
X 和观测量
Z
Z
Z 的联合概率等于条件概率乘以边缘概率:
P
(
X
,
Z
)
=
P
(
Z
∣
X
)
P
(
X
)
{P(X,Z) =P(Z \mid X) P(X)}
P(X,Z)=P(Z∣X)P(X)
式中:
P
(
Z
∣
X
)
P(Z|X)
P(Z∣X) 为观测量
Z
Z
Z 对应的概率;
P
(
X
)
P(X)
P(X) 是状态量
X
X
X 的先验概率。后验分布
P
(
X
∣
Z
)
P(X|Z)
P(X∣Z) 是一种常用且直观评估状态集和 观测集之间拟合程度的方法,我们求解期望的状态集可以由通过后验分布的最大化来实现,也就是极大验后估计:
X
^
=
arg
max
X
P
(
X
∣
Z
)
\hat{X}=\underset{X}{\arg \max } P(X \mid Z)
X^=XargmaxP(X∣Z)
有些文章用极大似然估计来介绍因子图优化,都可以,极大后验估计是极大似然估计在包含了先验“量测”后的特例,就多源融合导航而言,这两种最优估计没有本质上的区别。
用极大似然估计来理解:就视觉/惯性/GNSS 融合导航而言,不同传感器之间的量测,以及同一传感器在不同时刻的量测都是独立的,因此全局似然函数可以因式分解成关于各独立量测的似然函数的乘积。
基于因子图的状态估计方法正是将状态估计理解为对系统联合概率密度函数的极大验后估计问题。 一个系统可以描述为状态方程和量测方程两部分,并将状态误差和量测误差视为零均值白噪声即:
{
x
k
=
f
k
(
x
k
−
1
,
u
k
)
+
w
k
,
w
k
∼
N
(
0
,
Σ
k
)
z
k
=
h
k
(
x
k
)
+
v
k
,
v
k
∼
N
(
0
,
Λ
k
)
\left\{\begin{array}{rr} x_{k}=f_{k}\left(x_{k-1}, u_{k}\right)+w_{k}, & w_{k} \sim N\left(0, \Sigma_{k}\right) \\ z_{k}=h_{k}\left(x_{k}\right)+v_{k}, & v_{k} \sim N\left(0, \Lambda_{k}\right) \end{array}\right.
{xk=fk(xk−1,uk)+wk,zk=hk(xk)+vk,wk∼N(0,Σk)vk∼N(0,Λk)
根据正态分布的特性可以得到真实状态
k
x
k_x
kx 和理想量测
k
z
k_z
kz 的条件概率分布满足:
{
P
(
x
k
∣
x
k
−
1
)
∝
e
−
1
2
∣
f
k
(
x
k
−
1
)
−
x
k
∣
ε
k
2
P
(
z
k
∣
x
k
)
∝
e
−
1
2
∣
f
k
(
x
k
)
−
z
k
∥
k
2
\left\{\begin{array}{l} P\left(x_{k} \mid x_{k-1}\right) \propto e^{-\frac{1}{2}\left|f_{k}\left(x_{k-1}\right)-x_{k}\right|_{\varepsilon_{k}}^{2}} \\ P\left(z_{k} \mid x_{k}\right) \propto e^{-\frac{1}{2} \mid f_{k}\left(x_{k}\right)-z_{k} \|_{k}^{2}} \end{array}\right.
{P(xk∣xk−1)∝e−21∣fk(xk−1)−xk∣εk2P(zk∣xk)∝e−21∣fk(xk)−zk∥k2
实际中的状态量
X
X
X 往往是不知道的,而当前状态下的观测
Z
Z
Z 是知道的,也就是
P
(
Z
∣
X
)
P(Z|X)
P(Z∣X) 是知道的,因此在因子图模型中:
X
k
∗
=
arg
max
P
(
X
k
∣
Z
k
)
∝
arg
max
P
(
X
k
)
P
(
Z
k
∣
X
k
)
X_{k}^{*}=\arg \max P\left(X_{k} \mid Z_{k}\right) \propto \arg \max P\left(X_{k}\right) P\left(Z_{k} \mid X_{k}\right)
Xk∗=argmaxP(Xk∣Zk)∝argmaxP(Xk)P(Zk∣Xk)
其中,
X
k
=
{
x
0
:
k
}
X_{k}=\left\{x_{0: k}\right\}
Xk={x0:k} 是状态的集合,
Z
k
=
{
z
0
:
k
j
}
Z_{k}=\left\{z_{0:k}^j\right\}
Zk={z0:kj} 是所有状态下量测的集合。若系统服从马尔科夫假设,那么:
X
k
∗
=
arg
max
X
k
P
(
X
k
∣
Z
k
)
∝
arg
max
k
P
(
x
0
)
∏
k
[
P
(
x
i
∣
x
i
−
1
)
∏
m
i
m
i
[
P
(
z
i
j
∣
x
i
)
]
]
\begin{aligned} X_{k}^{*} & =\underset{X_{k}}{\arg \max } P\left(X_{k} \mid Z_{k}\right) \propto \underset{k}{\arg \max } P\left(x_{0}\right) \prod^{k}\left[P\left(x_{i} \mid x_{i-1}\right) \prod_{m_{i}}^{m_{i}}\left[P\left(z_{i}^{j} \mid x_{i}\right)\right]\right] \end{aligned}
Xk∗=XkargmaxP(Xk∣Zk)∝kargmaxP(x0)∏k[P(xi∣xi−1)mi∏mi[P(zij∣xi)]]
对式取对数得到后,将式代入式可以得到,系统的状态估计可等价为全局损失函数的联合优化:
X
∗
=
arg
min
X
∑
i
k
{
∥
f
i
(
x
i
−
1
,
u
i
)
−
x
i
∥
Σ
i
2
+
∑
j
=
1
m
j
∥
h
i
j
(
x
i
)
−
z
i
j
∥
Λ
i
j
2
}
X^{*}=\underset{X}{\arg\min } \sum_{i}^{k}\left\{\left\|f_{i}\left(x_{i-1}, u_{i}\right)-x_{i}\right\|_{\Sigma_{i}}^{2}+\sum_{j=1}^{m_{j}}\left\|h_{i}^{j}\left(x_{i}\right)-z_{i}^{j}\right\|_{\Lambda_{i j}}^{2}\right\}
X∗=Xargmini∑k{∥fi(xi−1,ui)−xi∥Σi2+j=1∑mj
hij(xi)−zij
Λij2}
上式即为基于因子图优化的估计的一般表达式,其左项为系统状态转移过程,右项为量测过程,
Σ
\Sigma
Σ 和
Λ
\Lambda
Λ 分别是状态转移过程和量测过程的协方矩阵,进行求解的是状态集合 X 。对于式,可以用下图进行表示:
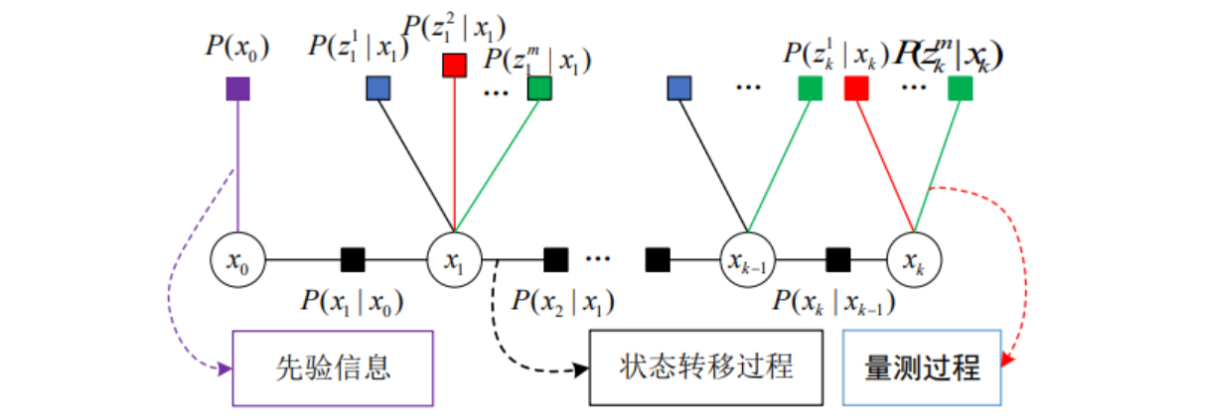
- 圆圈:变量节点,表示系统待估计的状态,对应一个变量 x x x 。
- 正方形:因子节点,表示先验信息、状态转移和量测过程,对应一个局部函数
f
f
f ,其中:
- 紫色 P ( x 0 ) P(x_0) P(x0) 为先验因子。
- 黑色 P ( x 1 ∣ x 0 ) … P ( x k ∣ x k − 1 ) P(x_1|x_0) \dots P(x_k|x_{k-1}) P(x1∣x0)…P(xk∣xk−1) 为状态转移,由上一时刻状态推测下一时刻状态。
- 其它为量测信息, P ( z ∣ x ) P(z|x) P(z∣x) 表示在参数 x x x 的条件下得到观测值 z z z。
- 线:当且仅当变量 x x x 是局部函数 f f f 的的自变量时,相应的变量节点和因子节点之间有一条边连接两个节点。
- 若在模型中加入其他传感器,只需将其添加到框架中相关的因子节点处即可。
利用因子图模型对估计系统的联合概率密度函数进行表示,可以直观地反映动态系统的动态演化过程和每个状态对应的量测过程。同时,图形化的表示使系统具有更好的通用性和扩展性。
3、因子图优化求解
每一个观测变量在上面贝叶斯网络里都是单独求解的(相互独立),所有的条件概率都是乘积的形式,且可分解,在因子图里面,分解的每一个项就是一个因子,乘积乘在一起用图的形式来描述就是因子图。 整个因子图实际上就是每个因子单独的乘积。 求解因子图就是将这些因子乘起来,求一个最大值,得到的系统状态就是概率上最可能的系统状态。
先找到残差函数
e
(
x
)
e(x)
e(x),由因子节点可以得到我们估计的值和实际的测量值之间的差值,即每个因子
f
f
f 会对应一个残差函数。根据中心极限定理,绝大多数传感器的噪声是符合高斯分布的,所以每个因子都是用高斯分布的指数函数来定义的。
g
(
x
)
=
1
2
π
σ
exp
(
−
(
x
−
μ
)
2
2
σ
2
)
g(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right)
g(x)=2πσ1exp(−2σ2(x−μ)2)
指数函数对应了残差函数,包括两个部分:系统状态量和观测量。 残差函数实际上表示的是用状态量去推测的观测量与实际观测量的区别。 残差函数的表达式一般都是非线性的,可以通过改变变量
X
X
X 来使残差函数最小化,残差函数最小,估计的值越符合观测值,套到因子图里面来看,因子图的求解是要所有因子的乘积最大化,
X
^
=
arg
max
X
∏
i
exp
(
−
1
2
∣
e
i
(
X
i
)
∣
Σ
i
2
)
\hat{X}=\underset{X}{\arg \max } \prod_{i} \exp \left(-\frac{1}{2}\left|e_{i}(X i)\right|_{\Sigma i}^{2}\right)
X^=Xargmaxi∏exp(−21∣ei(Xi)∣Σi2)
对于负指数函数形式,每一个因子乘积最大化代表里面的
e
(
x
)
e(x)
e(x) 最小化,对目标函数取对数,概论问题转为非线性最小二乘问题:
X
^
=
arg
max
X
∑
i
(
e
ϵ
˙
(
x
i
)
)
2
\hat{X}=\underset{X}{\operatorname{arg} \operatorname{max}} \sum_{i}\left(e_{\dot{\epsilon}}\left(x_{i}\right)\right)^{2}
X^=Xargmaxi∑(eϵ˙(xi))2
最优化问题可以选择高斯-牛顿法、列文博格-马夸尔特或者Dogleg等迭代优化算法求解,高斯-牛顿法比较简单,但稳定性较差,算法可能不收敛;列文博格-马夸尔特引入置信区间概念,约束下降的步长,提高稳定性,Dogleg也类似。**问题性质较好时可用高斯-牛顿法,问题条件恶劣时选择列文博格-马夸尔特或者Dogleg。**几种梯度下降方法比较如下:
- 最速梯度下降法:目标函数在 x k x_k xk 处泰勒展开,保留一阶项, x ∗ = − J ( x k ) x*= - J(x_k) x∗=−J(xk),最速下降法过于贪心,容易走出锯齿路线,反而增加迭代次数。
- 牛顿法:二阶泰勒展开,利用二次函数近似原函数。 H ∗ X = − J H*X= - J H∗X=−J,牛顿法需要计算目标函数的海森矩阵阵,计算量大。规模较大时比较困难。
- 高斯-牛顿法(GN): f ( x ) f(x) f(x) 进行一阶泰勒展开, f ( x ) f(x) f(x) 而不是 F ( x ) F(x) F(x) ,高斯牛顿法用雅各比矩阵 J J T JJ^T JJT 来作为牛顿法中二阶海森阵的近似, H X = g HX=g HX=g,在使用高斯牛顿法时,可能出现 J J T JJ^T JJT 为奇异矩阵或者病态的情况,此时增量稳定性较差,导致算法不收敛。
- 列文伯格–马夸尔特方法(LM):基于信赖区域理论,是由于高斯-牛顿方法在计算时需要保证矩阵的正定性,于是引入了一个约束,从而保证计算方法更具普适性。 ( H + λ I ) x = g (H+\lambda I)x=g (H+λI)x=g,当入较小时, H H H 占主导,近似于高斯牛顿法,较大时, λ ∗ I \lambda * I λ∗I 占主导,接近最速下降法。
4、Ceres 非线性最小二乘库
Ceres是一个用于求解非线性最小二乘问题的开源库,它可以用于许多优化和拟合问题。相关文档写的较为全面完善、原理也较为直观:http://ceres-solver.org/nnls_tutorial.html#numeric-derivatives。
Ceres 是一个用于求解各种非线性优化问题的开源 C++ 库, 它的设计理念是提供 一个通用、高效、灵活和易于扩展的优化库,各种非线性优化问题能够被快速构建并求 解。Ceres 求解的一般形式的最小二乘问题如下:
m
i
n
x
1
2
∑
i
ρ
i
(
∣
f
i
(
x
i
1
,
⋯
,
x
i
n
)
∣
2
)
s.t.
l
i
≤
x
j
≤
u
j
min {x} \frac{1}{2} \sum{i} \rho{i}\left(\left|f{i}\left(x{i{1}}, \cdots, x{i{n}}\right)\right|^{2}\right) \quad \text { s.t. } \quad l{i} \leq x{j} \leq u{j}
minx21∑iρi(∣fi(xi1,⋯,xin)∣2) s.t. li≤xj≤uj
该问题是一个带边界的核函数最小二乘问题,其中,
x
1
,
⋯
,
x
n
x_{1}, \cdots, x_{n}
x1,⋯,xn 在 Ceres 中被称为参数块 (Parameter Blocks),表示优化变量,
ρ
i
(
∥
f
i
(
x
i
1
,
⋯
,
x
i
n
)
∥
2
)
\rho_{i}\left(\left\|f_{i}\left(x_{i_{1}}, \cdots, x_{i_{n}}\right)\right\|^{2}\right)
ρi(∥fi(xi1,⋯,xin)∥2) 称为残差块 (Residual Blocks),
f
i
f_{i}
fi 称为代价函数 (Cost Function),表示误差项或约束项。
l
i
l_{i}
li 和
u
j
u_{j}
uj 分别表示
x
j
x_{j}
xj 的上下限,当
l
i
=
−
∞
,
u
j
=
∞
l_{i}=-\infty, u_{j}=\infty
li=−∞,uj=∞ 时,表示不限制
x
j
x_{j}
xj 的边界。目标函数由多个核函数
ρ
(
⋅
)
\rho(\cdot)
ρ(⋅) 求和构成,核函数 的自变量为误差项的平方。
ρ
i
\rho_{i}
ρi 也称为损失函数,主要用来消除异常点对求解过程的影响,通过抑制噪声的影响来获得较高的优化精度。若取
ρ
\rho
ρ 为恒等函数,如
ρ
(
s
)
=
s
\rho(s)=s
ρ(s)=s,则目标函数由多个误差项的平方和组成,得到无约束的最小二乘问题。
基本使用流程如下:
- 定义代价函数:首先,需要定义一个或多个代价函数,用于计算残差或误差的值。在此过程中,可以定义求导方式,包括自动求导(Auto Diff)、数值求导(Numeric Diff)和用户自定义的解析求导形式。
- 定义参数块:参数块表示需要优化的变量。Ceres 支持多种类型的参数块,包括一维数组、动态数组、特殊结构体和用户自定义类型等类型。在 SLAM 中,参数块通常被定义为四元数、李代数。添加参数块之前需要对定义好的参数块进行初始化,设定初始值。
- 定义问题对象:定义的问题对象可以用于管理代价函数和参数块。ceres 作用域下的 Problem 类包含多个成员函数,包括添加参数块函数、添加残差块函数、将某参数块设置为常量函数和设定参数块上下限函数等。
- 添加代价函数:使用 Problem 类中的成员函数将一个或多个代价函数添加到问题对象中。每个代价函数对应一个或多个参数块。
- 求解问题:求解问题通过调用 Solve 函数来实现。该函数的参数列表包括配置信息、问题对象指针和存储求解中各变量的信息的结构体的指针。配置信息定义在 Solver作用域下的 Options 结构体中,它的参数种类繁多,包括迭代求解方法、信赖域策略、求解器类型、最大迭代次数和最大求解时间等参数。通过 Ceres Solver 求解器求解非线性优化问题,最终输出优化后的变量。
Ceres 与 g2o 都是用于求解非线性优化问题的开源 C++库,但它们在设计理念和功能实现上有一些不同。g2o 的重点在于图优化,它专门用于解决图模型中的非线性优化问题。而 Ceres 则更注重于通用性,它可以用于解决各种类型的非线性最小二乘问题。
可以通过下面《视觉SLAM十四讲》中曲线拟合的示例来简单感受一下 Ceres 的使用:
#include <iostream>
#include <opencv2/core/core.hpp>
#include <ceres/ceres.h>
#include <chrono>
using namespace std;
// 代价函数的计算模型
struct CURVE_FITTING_COST {
CURVE_FITTING_COST(double x, double y) : _x(x), _y(y) {} // 成员列表初始化实现全残构造函数
// 残差的计算,模板仿函数
template<typename T>
bool operator()(
const T *const abc, // 模型参数,有3维
T *residual) const {
// 一维残差计算
residual[0] = T(_y) - ceres::exp(abc[0] * T(_x) * T(_x) + abc[1] * T(_x) + abc[2]); // y-exp(ax^2+bx+c)
return true;
}
const double _x, _y; // x,y数据
};
int main(int argc, char **argv) {
double ar = 1.0, br = 2.0, cr = 1.0; // 真实参数值
double ae = 2.0, be = -1.0, ce = 5.0; // 估计参数值
int N = 100; // 数据点
double w_sigma = 1.0; // 噪声Sigma值
double inv_sigma = 1.0 / w_sigma;
cv::RNG rng; // OpenCV随机数产生器
vector<double> x_data, y_data; // 数据
for (int i = 0; i < N; i++) {
double x = i / 100.0;
x_data.push_back(x);
y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma * w_sigma));
}
double abc[3] = {ae, be, ce}; // 定义估计变量 abc[3],传入初值 ae、be、ce
// 构建最小二乘问题
ceres::Problem problem; // 实例化 Problemn
for (int i = 0; i < N; i++) {
problem.AddResidualBlock( // 向问题中添加残差项
// 使用自动求导,模板参数:误差类型,输出维度,输入维度,维数要与前面struct中一致
new ceres::AutoDiffCostFunction<CURVE_FITTING_COST, 1, 3>(
new CURVE_FITTING_COST(x_data[i], y_data[i])
),
nullptr, // 核函数,这里不使用,为空。可以加核函数实现抗差
abc // 待估计参数,计算出的增量往 abc 里面加
);
}
// 配置求解器
ceres::Solver::Options options; // 这里有很多配置项可以填
options.linear_solver_type = ceres::DENSE_NORMAL_CHOLESKY; // 增量方程如何求解
options.minimizer_progress_to_stdout = true; // 输出到cout
ceres::Solver::Summary summary; // 优化信息
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
ceres::Solve(options, &problem, &summary); // 开始优化
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
cout << "solve time cost = " << time_used.count() << " seconds. " << endl;
// 输出结果
cout << summary.BriefReport() << endl;
cout << "estimated a,b,c = ";
for (auto a:abc) cout << a << " ";
cout << endl;
return 0;
}
5、GICI-LIB 中的图优化模型
1. 两种因子图结构
-
单历元结构(single-epoch structure ):如果我们不需要考虑历元之间的时间传播( time propagation ),使用单历元结构,每个历元独立求解最小二乘问题。
-
滑动窗口结构(sliding-window structure):如果需要考虑历元之间的时间传播作为约束,例如:INS 集成前的误差、速度模型、常值约束,使用滑动窗口结构,用窗口范围内很多历元的数据一起求解。滑动窗口内部被划分成两个区域,分别称为成熟区和成长区,相比于成长区内节点,成熟区和固定参考区内的运动状态节点被估计的次数更多,因而具有更高的估计精度。借用一张图来反映这种特点,与 GICI-LIB 不完全对应:
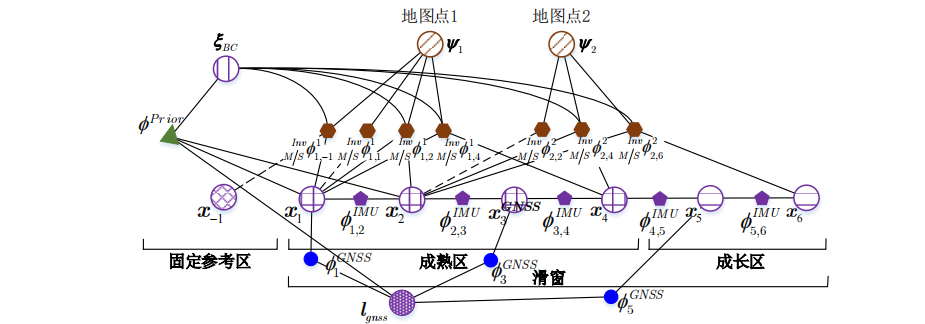
2. 边缘化 Marginalization
如果我们需要考虑历元间的状态传播,需要求解的最小二乘维度将一直增加,在实时定位中不能让维度一直增加下去,得想办法降维,一般都会定义一个最大滑动窗口区间长度来做维度限制。目前有两类主流的处理方法:
- 一是作为固定参考以消除不可观空间,又称基准自由度(gauge freedom),可以保留所有的视觉观测,即便视觉特征的跟踪长度已超出滑窗范围;但这种方法没有考虑被固定节点的不确定度,这会在一定程度上导致概率模型失真。
- 二是在状态节点滑出窗口之前,利用边缘化技术为下次优化构建新的先验残差函数。构建的先验残差函数具有一阶近似精度,相比于直接固定而言精度更高;但利用边缘化技术构建先验残 差函数的过程会导致额外的计算量,需要被移除的状态节点越多,计算量也就越大。通过边缘化技术构建的先验残差函数会引入线性化误差,且被固定参考关键帧运动状态节点的不确定度没有被考虑,因而估计结果是次优的。
在 GICI-LIB 中,采用边缘化技术,当先前的因子超出区间范围,会最小二乘求解,将之转变为先验信息(状态和方差),如下图所示: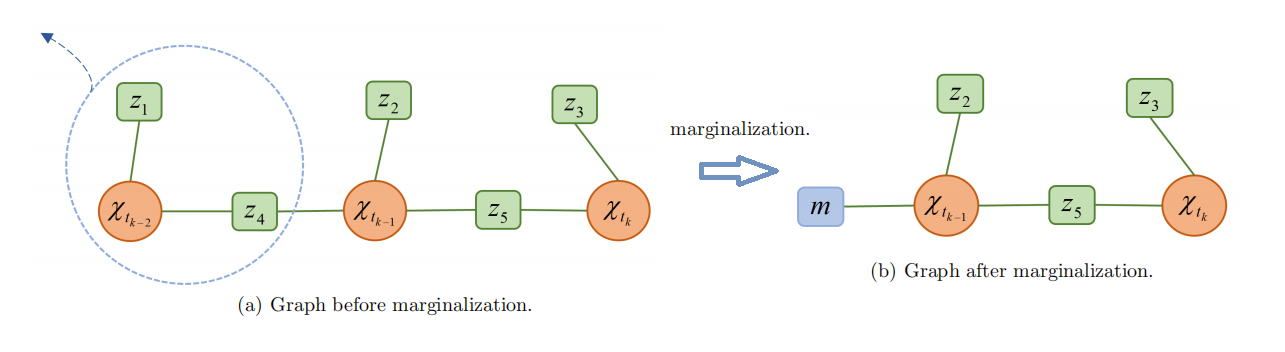
3. 关键帧 keyframes
视觉导航算法中广泛使用关键帧(keyframes)技术来稀释化(sparsification),以减小计算量。
在视觉估算中选择关键帧的原则是尽量跳过场景相似的帧。这些帧对解算的贡献较小,会导致估算参数的协方差出现无意义的下降。这一原则的本质是相邻帧中未建模误差之间的相关性很高,这使得将误差建模为白噪声是不正确的。对帧进行稀疏化处理可使误差白化,使其更符合 FGO 的基本假设。
此方法也可以用于 GNSS 中,其原始数据历元间也有相关性,且 GNSS 原始观测数据未建模误差的自相关特性主要是由多径引起的,相关时间取决于场景的变化率。下图显示了 GNSS 测量自相关性和稀疏化的影响。我们可以看到,相关时间随运动而变化,相关性对解算的影响也随运动而变化。相关性对解算的影响可以通过稀疏化得到缓解。
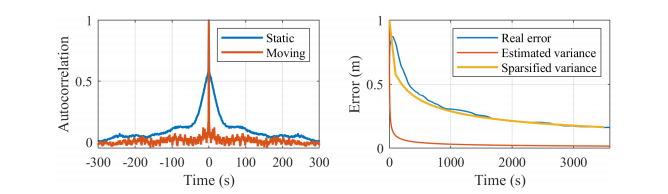
由于 GNSS 测量的相关时间会随时间变化,因此很难为稀疏化设置一致的时间步长。时间步长很难确定。不过,场景变化率与关键帧选择标准类似。因此,我们的 GNSS 稀疏策略设计为保留关键帧附近的测量值,而忽略其他测量值。
4. 图优化类 Graph
无论是哪一种因子图结构,我们都需要为每个量测定义残差、雅各比矩阵以及组成因子图的方法。这些都可以称之为因子(factors),因子用于构建变量节点之间的边和量测结点。GICI-LIB 中采用 OKVIS 中的 Graph 类实现图优化,完成各种操作。
5. 定位模式
GNSS

- Single Point Positioning(SPP):用单历元的伪距、多普勒测量值,解算接收机的位置、速度、钟差。只实现了单频非差伪距的 SPP,没做消电离层,因为多频组合要额外估计 IFB,模型复杂的同时也提高不了多少 SPP 的精度。
- Real-Time Differential(RTD):用单历元的双差伪距、非差多普勒测量值,解算接收机位置、速度。RTD 中可以很方便的使用多频观测值,因为 IFB 在双差中被大大消除,可以通过更改配置文件中 estimator 节点的输入项来设置。
- Real-Time Kinematic(RTK):用多历元的双差伪距,双差载波,非差多普勒观测值,计算接收机位置、速度。估计了单差模糊度,如果有 m 颗共视卫星、n 个共同频率,需要估计 m × n m \times n m×n 个单差模糊度。除了图优化估计,RTK 还有模糊度固定的步骤,GICI-LIB 支持部分模糊度固定。
- Precise Point Positioning(PPP):使用非差的伪距、载波、多普勒观测值,估计接收机速度、位置、钟差、大气延迟、IFB。GICI-LIB 支持 PPP-AR,但没有完全测试,由于 PPP 比 RTK 浮点解的噪声更大,想固定必须要有偏差产品,并进行改正。
- Global Frame Initialization:纯 GNSS 解算在 ECEF 框架进行,而进行组合需要在 ENU 框架进行,因此需要进行转换。全局框架初始化定义一个基准点,用于将 ECEF 框架中的状态转换为 ENU 框架中的状态。基准点也可用于计算重力加速度,用于惯导惯导。设置基准点有两种方法:
- 我们运行 SPP 估计,将基准点设置为该估计的第一个有效解。
- 如果将
force initial global position选项设置为 true,我们通过initial global position选项从配置文件中加载点坐标。
GNSS+ INS
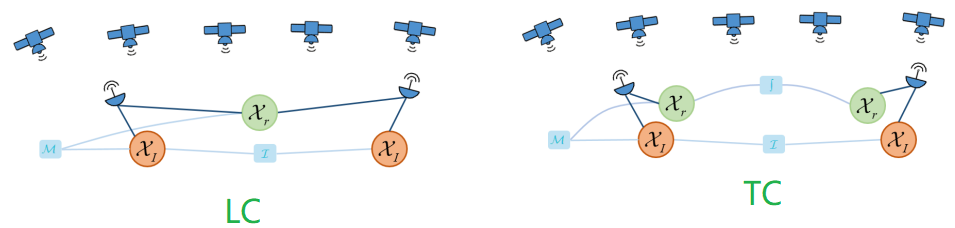
- Loosely Integration(LC):GNSS/INS 松组合用 GNSS 解算结果(位置、速度),和 INS 的原始数据(比力、角增量)进行组合解算。
- Tightly Integration(TC):GNSS/INS 紧组合用 GNSS 的原始数据(伪距、载波、多普勒),和 INS 的原始数据(比力、角增量)进行组合解算。
- Initialization:GNSS/INS 初始化会估计速度、位置和偏差;为了提高效率,无论松紧组合都使用松组合的方程。先用加速度计比力量测值计算俯仰角和横滚角,当有足够比力量测值之后再对航向角进行估计,因子图结构与松组合一致,不同的是,我们使用多普勒来计算初始位置的增量,因为初始位置噪声过大,而多普勒噪声较低。
GNSS + INS + Camera
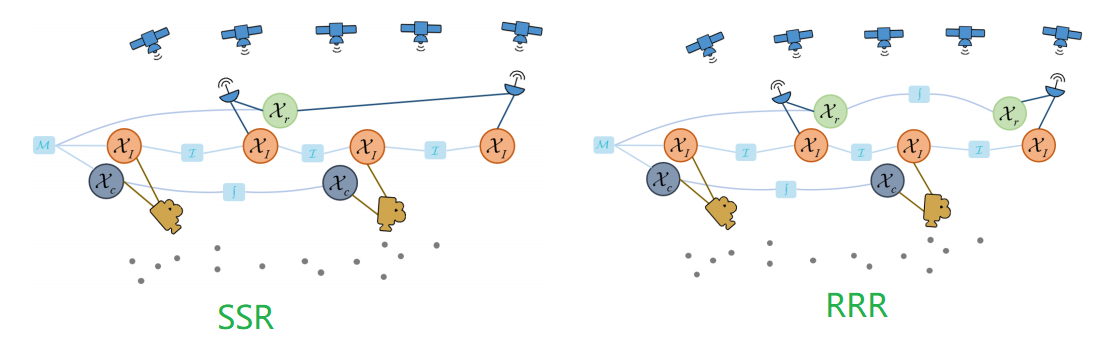
摄像机状态之间没有相互联系,因为相应的参数是时变的。我们在图中保留了连接,以表示由于跟踪地标的切换,各次的估计参数会发生变化。
- Solution/Raw/Raw Integration(SRR):SRR 采用 GNSS 的解算结果(速度、位置),和 INS 的原始数据(比力、角增量),以及 Camera 数据(特征点),进行组合解算。
- Raw/Raw/Raw Integration(RRR):RRR 采用 GNSS 的原始数据(伪距、载波、多普勒),和 INS 的原始数据(比力、角增量),以及 Camera 数据(特征点),进行组合解算。
- Initialization:GNSS/INS/Camera 初始化位置、速度、偏差、特征点位置。分两步进行,先进行 GNSS/INS 初始化,再通过空间交汇对特征点追踪。
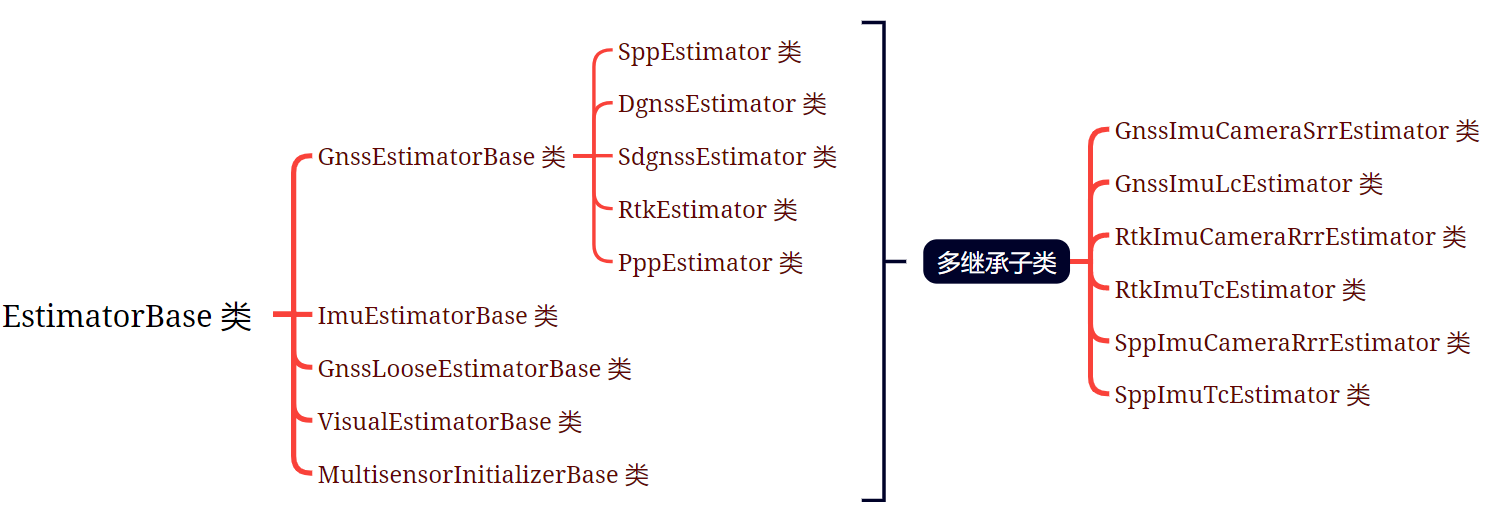
Estimator 类型封装
GICI-LIB 提供的多种传感器在不同定位模式下的很多因子,并封装了一个基类,为所有传感器提供基础的函数去操作变量因子和量测因子,具体可以看各种 xxx_estimator_base.h,看算法的时候肯定重点要看这些文件。
ization**:GNSS/INS/Camera 初始化位置、速度、偏差、特征点位置。分两步进行,先进行 GNSS/INS 初始化,再通过空间交汇对特征点追踪。
Estimator 类型封装
GICI-LIB 提供的多种传感器在不同定位模式下的很多因子,并封装了一个基类,为所有传感器提供基础的函数去操作变量因子和量测因子,具体可以看各种 xxx_estimator_base.h,看算法的时候肯定重点要看这些文件。
[外链图片转存中…(img-XVaLuo6n-1695806367896)]