顾名思义就是使用链式存储来实现的二叉树,因为二叉树是递归定义的,所以二叉树的实现中,都是会使用递归来完成.这里面需要一些前置的二叉树理论知识,对这部分不是很理解的可以先看下这篇二叉树的概念.

下面开始进入正题了:

---

1.二叉树的创建

        假定现有"ABD##E#H##CF##G##"这样的一组的数据,'#'代表为NULL,意味着其为空结点.使用前序遍历的方式来完成二叉树的创建.

        首先要知道二叉树要看成三个部分: 根,左子树,右子树,树的每个结点都可以看作是根,向下分出的子结点是左右子树,左,右子树再分别继续看成是根,左子树,右子树,一直分叉下去,直到空.

        前序遍历可以说是深度优先的遍历方式,遍历的顺序是根->左子树->右子树.

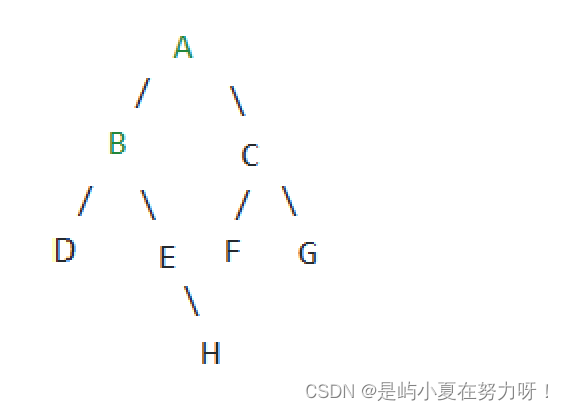
        这是通过上面一组数据而画的树的图,从根节点从'A'开始,分出左子树'B',以左子树为根,又分出左子树'D',此时遇到了两个'#'代表结点的左右子树为空,开始返回到开始的'B'结点,分出右子树'E',以右子树'E'为根,左树遇到了'#'代表'E'的左子树为空,继续分出右子树'H',以'H'为根结点,此时遇到了两个'#'表示左右子树为空,开始回到最初的根节点'A'.

        此时左子树已经遍历生成完了.回到了最开始的'A'根结点,'A'分出右子树'C',以'C'为根节点分出左子树'F',遇'#',表示子节点为空,'F'的左右子树为空,回到'C'结点,分出右子树'G',遇'#',表示子节点为空,此时数据走完,树也就创建好了.

        这里理解起来可能比较复杂,需要自己多画图理解几遍,因为树的内容比较抽象.把树分成根,左子树,右子树,理解了这个,上述遍历应该就问题不大了.

下面是代码的实现:

typedef struct TreeNode
{
	struct TreeNode* left;
	struct TreeNode* right;
	int val;
}Node;
 
//构建先序二叉树
Node* constructTree(char* a, int* i) 
{
	if (a[(*i)] == '#')
	{
		(*i)++;
		return NULL;
	}
	Node* root = (Node*)malloc(sizeof(Node));
	root->val = a[(*i)];
	(*i)++;

	root->left = constructTree(a, i);
	root->right = constructTree(a, i);
	return root;
}

整体的逻辑就是: 

        首先判断当前字符是否为'#'，如果是，则将指针i向后移动一位，并返回空指针，表示当前节点为空。

        如果当前字符不是'#'，则创建一个新的节点，并将当前字符赋值给节点的val属性。然后将指针i向后移动一位。

        接下来，递归调用constructTree函数构建节点的左子树，将返回的节点赋值给当前节点的left属性。

        再次递归调用constructTree函数构建节点的右子树，将返回的节点赋值给当前节点的right属性。

        最后，返回根节点。

        这样，通过递归调用constructTree函数，可以根据给定的字符数组构建一棵二叉树

---

2二叉树的前,中,后序遍历

        所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。

        遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。因此理解和掌握二叉树是极其重要的,着会帮助你能更好的明白树的结构和后面树的更加复杂的运算.

前序/中序/后序的递归结构遍历：

1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

        由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。

上述都是遍历的一些理论知识,说明了树遍历方式的方式还是很多的,下面开始进入实战部分:

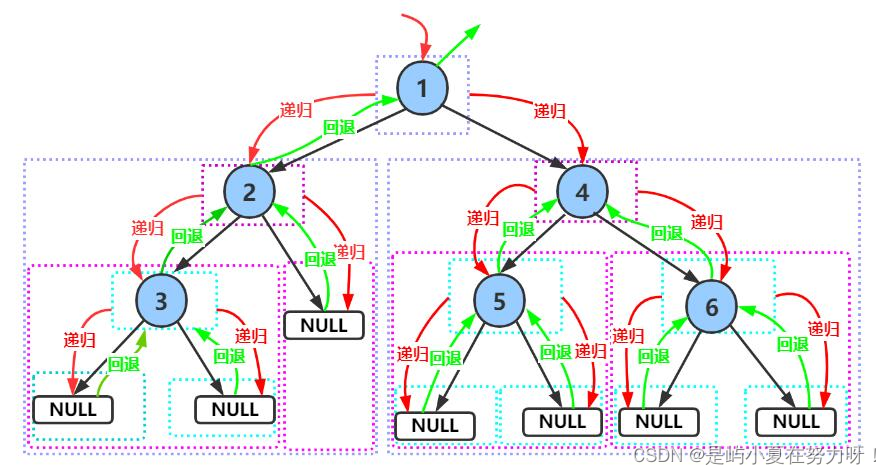
        如图所示,顺序是:根->左子树->右子树.

        遍历到一个结点后,继续以此结点为根,遍历左子树,直到一直递归到空,开始返回,再开始遍历右子树.这个图需要大家好好理解一下,可以利用图来明白树的遍历究竟是怎么回事.

        明白了树的前中后序是怎么回事,就可以开始着手来写代码实现了.

//前序
void Preorder(BTnode* root)
{
	if (root == NULL)
		return;
	printf("%c", root->val);
	Preorder(root->left);
	Preorder(root->right);
}

//中序 
void Inorder(BTnode* root)
{
	if (root == NULL)
		return;
	Inorder(root->left);
	printf("%c", root->val);
	Inorder(root->right);
}

//后序
void Postorder(BTnode* root)
{
	if (root == NULL)
		return;
	Postorder(root->left);
	Postorder(root->right);
	printf("%c ", root->val);
}

        首先判断树为不为空,为空就返回,没必要再往下递归了.当不为空,根据前中后序的不同,遍历的顺序也就不相同, 

1.         前序:根->左子树->右子树
2.         中序:左子树->根->右子树
3.         后序:左子树->右子树->根         

        前中后序遍历的代码实现,可以直观的看到通过修改递归左右子树的顺序,就可以完成对前中后序的遍历.

---

3.层序遍历

        上面咱们对前(先)序遍历、中序遍历、后序遍历进行了讲解，除此之外还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。
        这里的层序遍历和前中后序不同的是,它是一种自上而下,从左到右的遍历方式,以根结点开始,一层一层往下.

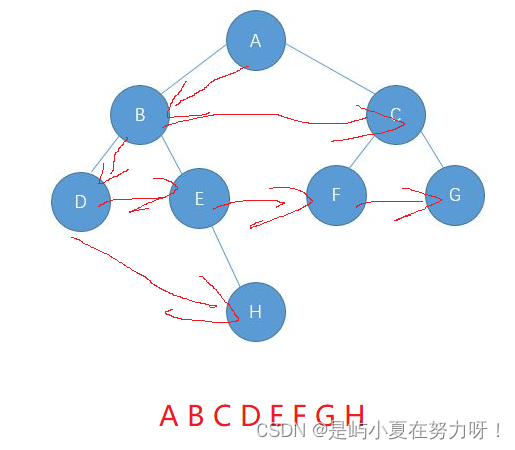
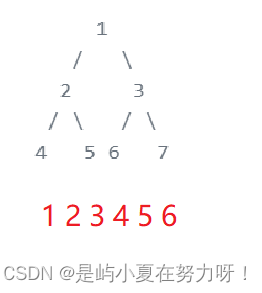
        如图所示,层序的遍历的遍历方式就是这样.理解了层序遍历的方式后,下一步就是写代码俩实现它了.这里因为层序遍历的特殊性,因此需要借助队列来完成.

void Leveloder(BTnode* root)
{
	Queue q;
	QueueInit(&q);

	if (root)
		QueuePush(&q, root);

	while (!QueueEmpty(&q))
	{
		BTnode* front = QueueFornt(&q);
		printf("%d ", front->val);

		if (front->left)
			QueuePush(&q, front->left);
		if (front->right)
			QueuePush(&q, front->right);

		QueuePop(&q);
	}
	printf("\n");
}

        队列的特性是:先进先出.可以利用这一特点,先将根结点入队,取出队头的结点,然后再入左右子结点.

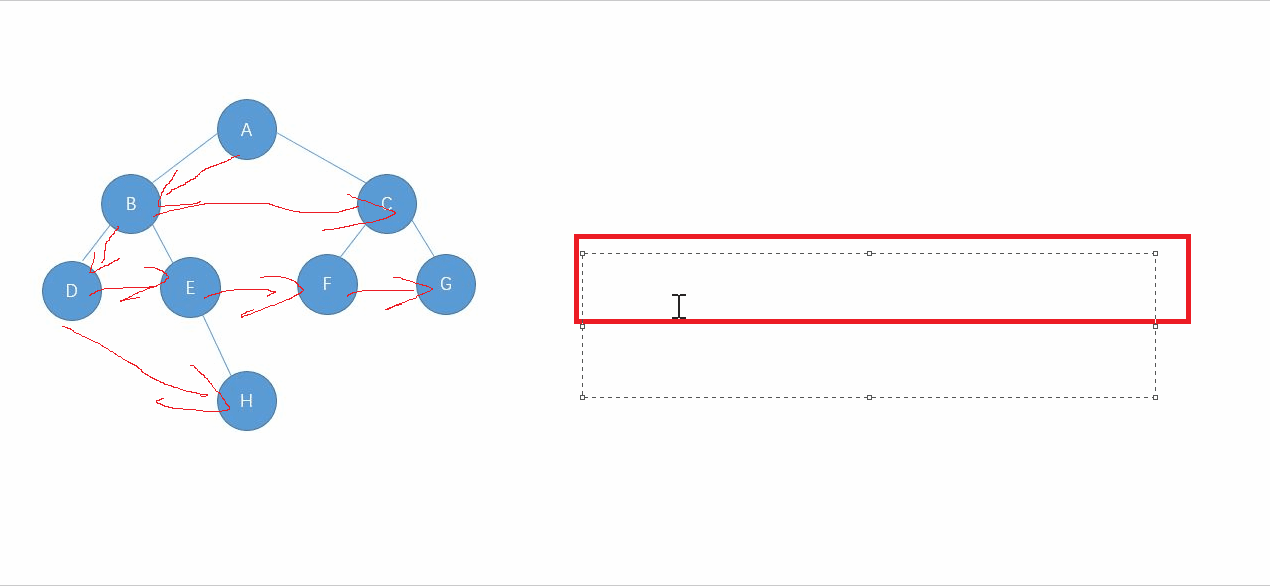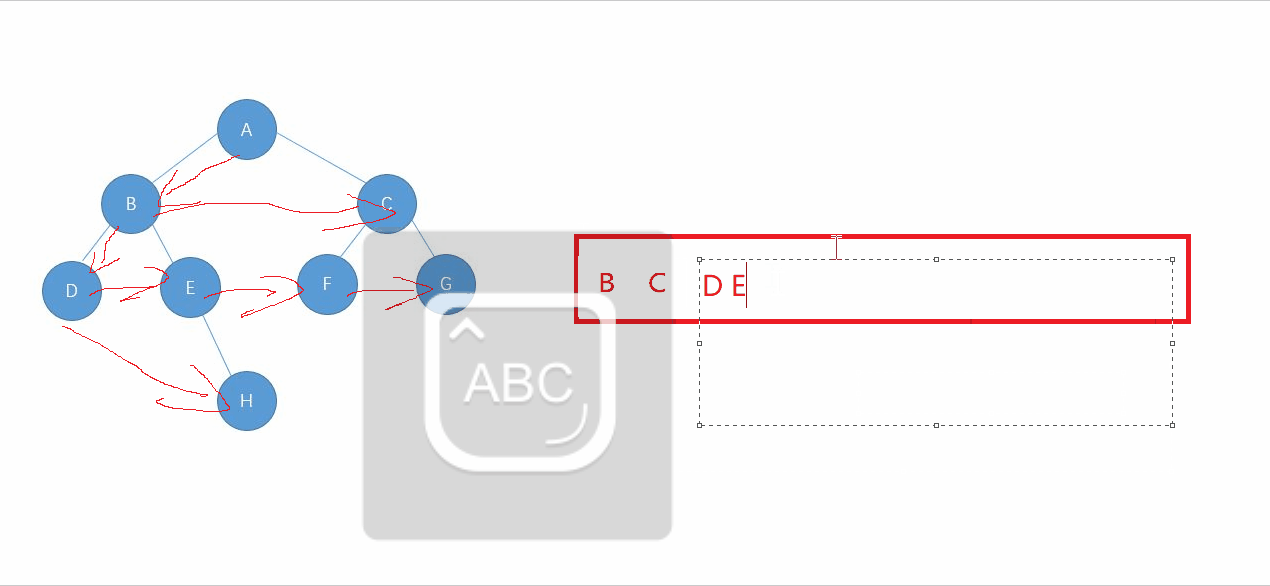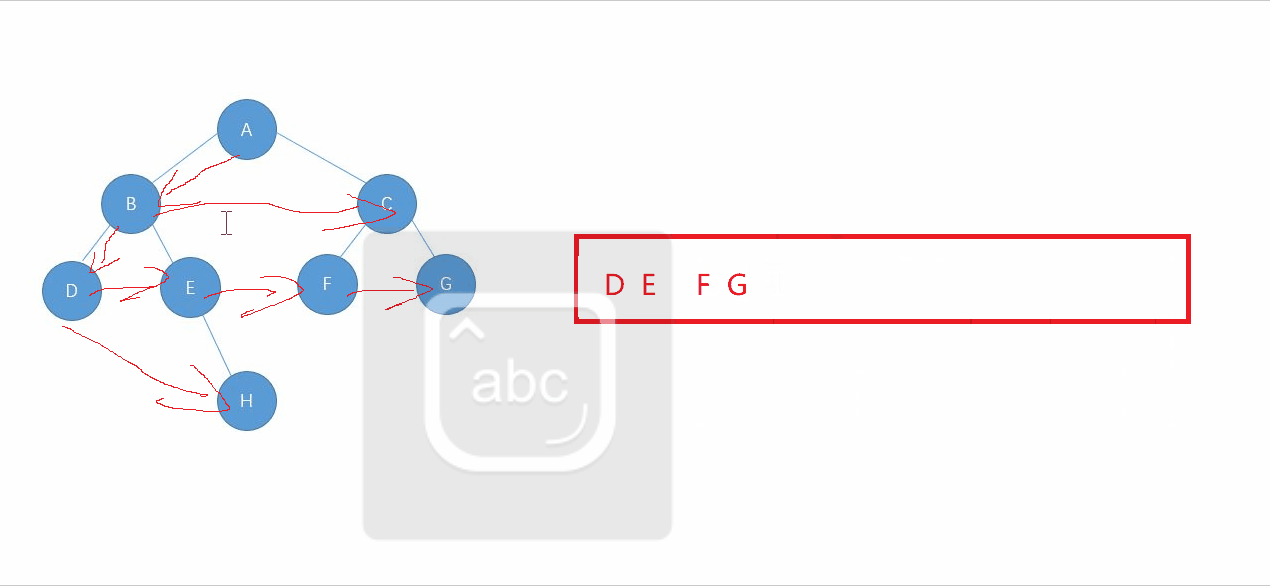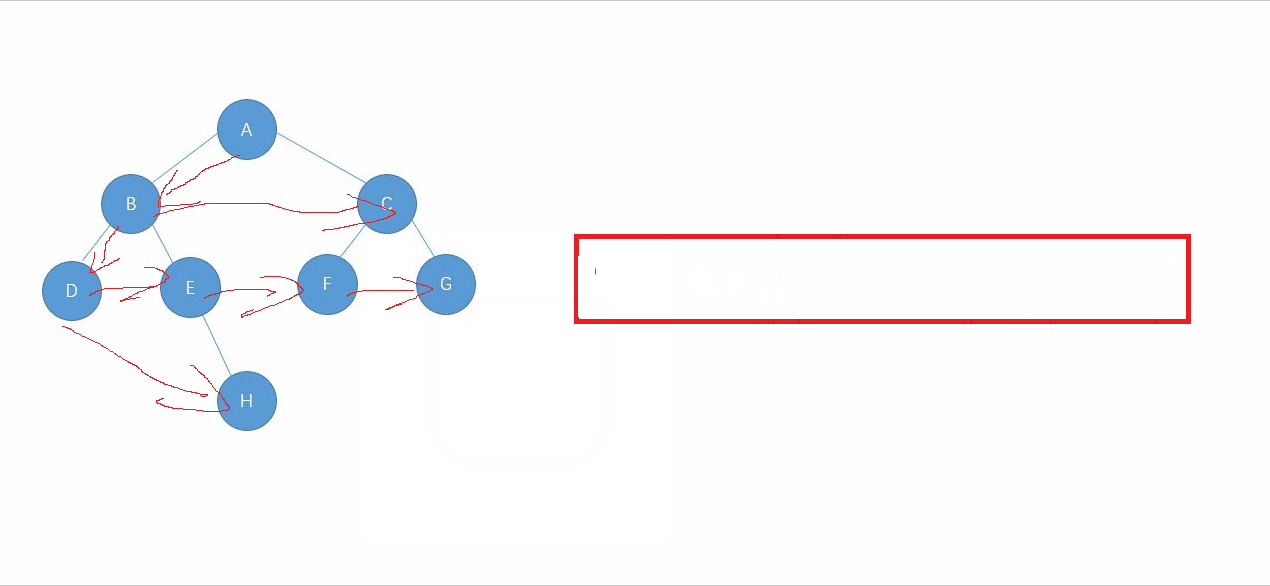
        开始的时候队列为空,往队中push根结点,取出结点,此时队列为空,往队中push左右子结点,然后pop掉队头的数据,此时第一层就遍历完了.发现了嘛,聪明的你一定看出来了吧,上一层遍历完的时候,会把下一层的结点都push到队列中,上一层遍历完,队中放的数据就是下一层的结点数据.

---

4.结点个数及高度

        接下来的这些都是在二叉树的遍历基础上进行稍微的改变,利用二叉树的遍历机制,我们可以干更多的事情.

4.1二叉树的结点个数

        结点个数就是统计这颗二叉树有多少个结点,即树的枝叶有多少.这里可以使用上面遍历的任意一种方式来得出.

int TreeSize(BTnode* root)
{
	if (root == NULL)
		return 0;

	return TreeSize(root->left) + TreeSize(root->right) + 1;
}

        首先判断根节点是否为空，如果为空，则说明该树为空树，节点个数为0，直接返回0。如果根节点不为空，那么递归地调用TreeSize函数来计算左子树和右子树的节点个数，然后将左子树节点个数和右子树节点个数相加，再加上根节点本身，即可得到整个二叉树的节点个数。

4.2二叉树叶子结点个数

        叶子结点,即这个结点没有子结点.

int TreeLeafSize(BTnode* root)
{
	if (root == NULL)
		return 0;
	else if (root->left == NULL && root->right == NULL)
		return 1;
	else
		return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

        首先判断根节点是否为空，如果为空，则说明该树为空树，叶子节点个数为0，直接返回0.接下来判断根节点是否为叶子节点，即左子树和右子树都为空。如果是叶子节点，则返回1。如果根节点不是叶子节点，那么递归地调用TreeLeafSize函数来计算左子树和右子树的叶子节点个数，然后将左子树叶子节点个数和右子树叶子节点个数相加，即可得到整个二叉树的叶子节点个数。

4.3二叉树第k层结点个数

        树通过形状我们可以知道,它是分层的,上面我们学会了树的层序遍历,理解了层序遍历,要求第k层的结点树还是没那么难的.

第k层的节点
int BinaryTreeLevelKSize(BTnode* root, int k)
{
	assert(k > 0);
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return BinaryTreeLevelKSize(root->left, --k) + BinaryTreeLevelKSize(root->right, --k);
}

        

        先使用assert函数来断言k的值大于0，确保k是一个合法的层数。然后判断根节点是否为空，如果为空，则说明该树为空树，第k层的节点个数为0，直接返回0。如果k等于1，说明此时的结点是在k层上的,因此返回1。往下递归调用左子树和右子树,这里的--k,递归到下一层,k的层数就跟着减减.

        假设k的层数是3,要求第三层的结点个数,利用--k,当k为1的时候表明此时已经到了指定的层数,因此开始返回1.

4.4二叉树查找值为x的结点

        相当于是遍历这棵树,找到与之符合的值,并返回此结点的地址.

//查找值为x的节点
BTnode* TreeFind(BTnode* root, TreeData x)
{
	if (root == NULL)
		return NULL;
	if (root->val == x)
		return root;

	BTnode* ret = NULL;
	ret = TreeFind(root->left, x);
	if (ret)
		return ret;

	ret = TreeFind(root->right, x);
	if (ret)
		return ret;
	return NULL;
}

         首先判断根节点是否为空，如果为空，则说明该树为空树，直接返回NULL。

        然后判断根节点的值是否等于x，如果等于x，则说明找到了目标节点，直接返回根节点的指针。

        如果以上条件都不满足，说明目标节点可能在左子树或右子树中，那么递归地调用TreeFind函数来在左子树和右子树中查找值为x的节点。

        再在左子树中查找，将返回的节点指针保存在ret变量中，然后判断ret是否不为空，如果不为空，则说明在左子树中找到了目标节点，直接返回ret。

        如果在左子树中没有找到目标节点，则继续在右子树中查找，将返回的节点指针保存在ret变量中，然后判断ret是否不为空，如果不为空，则说明在右子树中找到了目标节点，直接返回ret。

        左子树和右子树中都没有找到目标节点，则说明目标节点不存在于该二叉树中，返回NULL。

---

5.销毁

        二叉树的销毁并不能够直接free掉根结点,因为当根结点给释放后,就再也找不到左右子树了,因此需要从树的底部开始free,最后再free掉根结点.这里的销毁还是使用递归的方式来实现.

void TreeDestory(BTnode* root)
{
	if (root == NULL)
		return;

	TreeDestory(root->left);
	TreeDestory(root->right);

	free(root);
}

        结点为空就返回,不为空继续往下走,走到叶子结点,free掉,再递归回去,一直到根结点.

        这里的销毁其实和二叉树的后序遍历很相似,左子树走完,走右子树,最后再是根.

---

        以上就是本篇的所有内容啦,希望能够让你对二叉树的理解提升一个台阶,可以的话一键三连十分感谢,家人们的支持是我前行的最大动力。