一、题目大意
我们有一台起重机的机械臂,它由多个节相连组成,如下所示。

起初的时候,所有的节之间的角度都是180度,是竖直的,我们可以扭转其中任意两个节的角度,每一次移动后题目需要输出题目最后一个点相对于第一个点偏移的x和y如下两张图所示。


其中 ,然后
。
从图中其实可以推断一个猜想,我们对1和2之间角度偏移了30°,那么2后面的3,4,5其实都会偏移2,即对于[1,n]个节,偏移 i-1 到i 的角度,那么[i,n]其实都要偏移同样的角度。
二、解题思路
其实不难看出了,这是一个区间操作的问题,那么考虑下,假如说我有10000节,我把第一节和第二节之间的角度偏移到210,动了30度,那么除了第二节,后面的9997节其实也会都再偏移30度,假设我们从0开始计下标,那么除了下标为0的元素不用改,其他[1,10000)的下标的元素都得变!如果一个一个更新,那么复杂性太高了,如果操作10000次,那么就是10000*10000*10000次的数组更新,分钟甚至小时的时间蜗牛速度!所以就考虑下区间操作,是不是可以不更新所有的点!
我们可以构建一个线段树,每个节点保存3个值,如下
1、节点相对它起点的偏移的x
2、节点相对于它终点偏移的y
3、节点的子节点共同偏移的角度angle
这样的话我们要更新第[2,10000]的元素也就是[0,10000)下标的数组的值的话,如果使用线段树会快很多,10000的线段树有10多层,我就画一个简要的图,例如下图,我们更新画红圈圈的两个点就可以代表对[2048,8192)这6000多个数组元素进行赋值,那么有了它,其实本题目就可以在O(n*n*logn)的复杂性完成。

那么如何实现区间修改角度呢,拿一个之后4个元素的起重机,假设它们的长度都是5,那么每个节点需要记录的值有几部分。
1、它管理的区间[l,r)
2、它相对于它起点x偏移和y偏移(x,y)
3、它的所有子节点一起动过的角度 dAngle
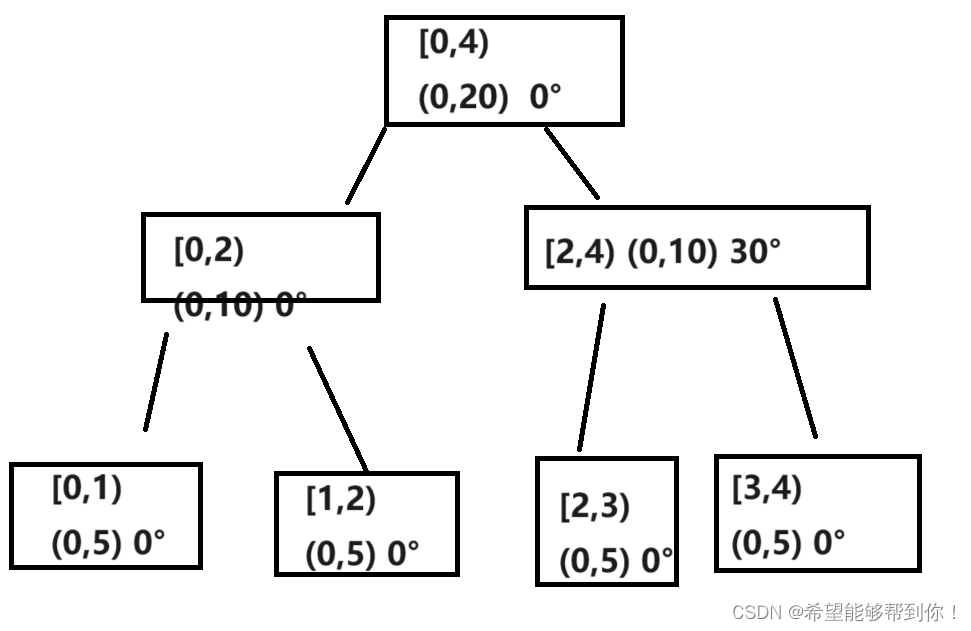
假如说我们要对1到2节点的角度进行改变,从180到210变化30,那么对于线段树的变化如下。

这个更新的步骤如下,假设旋转的角度为 i-1到 i 转 Ω度,
1、如果节点的 [l,r) 中 l > i 或者 r <= i,直接跳过
2、如果节点的 [l,r)中 l>=i,那么更新这个节点的x和y为转动Ω度后的x和y,同时记录之前的x和y为x_和y_,然后这个节点dAngle的度数增加30,代表它的子节点都偏移30度,然后直接向上去更新父节点,更新父节点时,先用它原来的x_和y_旋转父节点的dAngle度,之后用父节点的值减去求出的值,然后用子节点新的值x和y也去旋转父节点的dAngle度,之后父节点的值加上这个值。
然后递归的更新父节点的父节点,每次更新父节点时,用它直接相连的子节点变化之前的值,偏移父节点的dAngle度,然后父节点的值减去这个值,之后计算直接相连的子节点的值变化之后的值,偏移父节点的dAngle度,然后父节点的值加上这个值。
一直利用上一段的操作,更新到根节点即可。
3、如果节点的 l < r,那么代表这个节点中的子节点会完全包含,则递归它的两个子节点。
之后我们要输出答案的时候,只需要输出根节点的x和y的偏移量即可。
那么还有有点就是如何去计算某个x和偏移了Ω角度后的值,其实不难,例如将x1和y1原来的角度时Ω1度,旋转Ω2度到x2和y2,如下所示。

那么我们不难看出这像是两个斜边相同的直角三角形,然后我们还知道Ω1、Ω2、x1和x2的值,那么我们根据斜边相同的等值关系去列方程
x1/sin(Ω1) = x2/sin(Ω1+Ω2)
y1/cos(Ω1) = y2/cos(Ω1+Ω2)
解出这个二元一次方程,求出x2和y2即可,化简下。
然后我们直到tan(Ω1)=x/(-y),那么其实也就可以看出,求出x2和y2不需要知道x1和y1之前偏移的角度,只需要直到在某次操作时,变化的角度即可。
然后需要注意的是,计算三角函数,需要特殊处理下90°的倍数,
1、当变化90°时,其实就是 x2=y1*(-1),y2=x1
2、变化180°时,x2=x1*(-1),y2=y1*(-1)
3、变化270°时,就是x2=y1,y2=(x1)*(-1)
然后变化的角度小于0就加上360即可,大于0就对360取余(多转一圈少转一圈x和y没有变化)
然后计算tan时,需要考虑下之前x1和y1是不是有一方为0。如果都是0,那么不用计算了,怎么转都是0,
如果x1==0,y1!=0,那么转之后 x2=y1 * sin(Ω2) * (-1),y2=y1 * cos(Ω2)
如果x1!=0,y1==0,那么转之后 x2=x1 * cos(Ω2) * (-1),y2=x1 * sin(Ω2)
然后注意下,我以上说的Ω1是之前的角度,Ω2是之后的角度-之前的角度的差,就是我们需要根据输入来计算的,不是直接用的输入的那个角度。
三、代码
#include <iostream>
#include <cmath>
using namespace std;
// 节点i相对于它的起点的x,y偏移就等于datX[i],datY[i]再旋转上它所有父节点的datAngle的和
double datX[32780], datY[32780], num[10007], tmpX, tmpY, pai = 3.141592653589793;
int n_, n, angle[10007], op, datAngle[32780];
void input()
{
for (int i = 0; i < n_; i++)
{
scanf("%lf", &num[i]);
angle[i + 1] = 180;
}
}
void init()
{
n = 1;
while (n < n_)
{
n = n * 2;
}
for (int i = ((2 * n) - 2); i >= 0; i--)
{
if (i >= (n - 1))
{
datX[i] = 0.0;
datAngle[i] = 0;
if ((i - (n - 1)) < n_)
{
datY[i] = num[i - (n - 1)];
}
else
{
datY[i] = 0.0;
}
}
else
{
datAngle[i] = 0;
datX[i] = datX[(i * 2) + 1] + datX[(i * 2) + 2];
datY[i] = datY[(i * 2) + 1] + datY[(i * 2) + 2];
}
}
}
void calcVal(int dAngle, double currentX, double currentY)
{
if (dAngle == 0)
{
tmpX = currentX;
tmpY = currentY;
}
else if (currentX == 0.0 && currentY == 0.0)
{
tmpX = currentX;
tmpY = currentY;
}
else if (dAngle == 90)
{
tmpX = currentY * (-1.0);
tmpY = currentX;
}
else if (dAngle == 180)
{
tmpX = currentX * (-1.0);
tmpY = currentY * (-1.0);
}
else if (dAngle == 270)
{
tmpX = currentY;
tmpY = currentX * (-1.0);
}
else if (currentX == 0.0)
{
double omiga = ((dAngle * (1.0)) / (180.0)) * pai;
tmpX = sin(omiga) * currentY * (-1.0);
tmpY = cos(omiga) * currentY;
}
else if (currentY == 0.0)
{
double omiga = ((dAngle * (1.0)) / (180.0)) * pai;
tmpX = cos(omiga) * currentX;
tmpY = sin(omiga) * currentX;
}
else
{
double omiga = ((dAngle * (1.0)) / (180.0)) * pai;
tmpX = cos(omiga) * currentX + (sin(omiga) * (currentY / currentX) * (-1.0) * currentX);
tmpY = cos(omiga) * currentY - (sin(omiga) * (currentX / currentY) * (-1.0) * currentY);
}
}
//[l,n)
void handle(int idx, int dAngle, int i, int l, int r)
{
if (idx <= l)
{
double beforeChangeX = datX[i];
double beforeChangeY = datY[i];
calcVal(dAngle, beforeChangeX, beforeChangeY);
double afterChangeX = tmpX;
double afterChangeY = tmpY;
datX[i] = afterChangeX;
datY[i] = afterChangeY;
datAngle[i] = (datAngle[i] + dAngle) % 360;
int j = i;
while (j > 0)
{
j = (j - 1) / 2;
calcVal(datAngle[j], beforeChangeX, beforeChangeY);
beforeChangeX = datX[j];
beforeChangeY = datY[j];
datX[j] = datX[j] - tmpX;
datY[j] = datY[j] - tmpY;
calcVal(datAngle[j], afterChangeX, afterChangeY);
datX[j] = datX[j] + tmpX;
datY[j] = datY[j] + tmpY;
afterChangeX = datX[j];
afterChangeY = datY[j];
}
}
else if (l < idx && r > idx)
{
handle(idx, dAngle, i * 2 + 1, l, (l + r) / 2);
handle(idx, dAngle, i * 2 + 2, (l + r) / 2, r);
}
}
int main()
{
int nAngle, idx, cnt = 0;
while (~scanf("%d%d", &n_, &op))
{
if (cnt > 0)
{
printf("\n");
}
input();
init();
for (int i = 0; i < op; i++)
{
scanf("%d%d", &idx, &nAngle);
if (nAngle != angle[idx])
{
int dAngle = nAngle - angle[idx];
if (dAngle < 0)
{
dAngle = dAngle + 360;
}
handle(idx, dAngle, 0, 0, n);
angle[idx] = nAngle;
}
printf("%.2f %.2f\n", datX[0], datY[0]);
}
cnt++;
}
return 0;
}四、运行情况