目录
编辑
一,优先级队列
二,实现
1.构造priority_queue类
2.简单的top()与size()还有empty()函数
3.push函数
4.pop函数
5.构造函数
6.测试
三,仿函数
1.介绍
2.使用
一,优先级队列
优先级队列——priority_queue。这个结构体类型也是C++里面的一个非常好用的一个数据结构。可以在Cplusplus网站上看看这个数据结构的介绍:
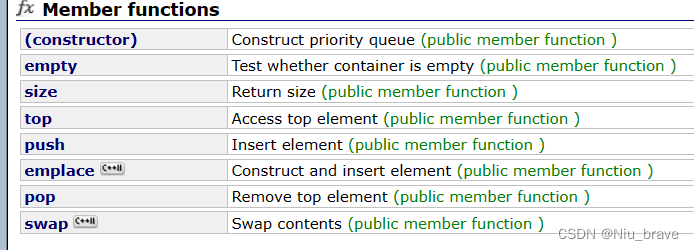
在这一项介绍中可以看到这个数据结构类型的各种模板。因为我们要实现一个priority_queue所以我们就要来看看这个数据结构类型的各种函数,如下:
今天我们只会实现size,top,push,pop,还有一个construct的迭代器构造函数。在这里还要声明一点,这个数据结构类型的地城原理其实就是一个堆,也就是heap。
二,实现
1.构造priority_queue类
实现步骤如下,首先开一个.h文件。然后写下如下代码:
#include<iostream> 2 using namespace std; 3 4 namespace area 5 { 6 template<class T,class Container> 7 class priority_queue 8 { 9 public: 10 11 12 private: 13 Container _con; 14 15 }; 16 17 }因为这个优先级队列实现的原理和堆实现的原理相像,所以可以先传一个缺省参数vector<T>给Container。如下:
#include<iostream> 2 using namespace std; 3 #include<vector> 4 5 namespace area 6 { 7 template<class T,class Container=vector<T> > 8 class priority_queue 9 { 10 public: 11 12 13 private: 14 Container _con; 15 16 }; 17 18 }
2.简单的top()与size()还有empty()函数
这两个函数实现起来比较简单,所以可以先来实现一下,实现代码如下:
#include<iostream> 2 using namespace std; 3 #include<vector> 4 5 namespace area 6 { 7 template<class T,class Container=vector<T> > 8 class priority_queue 9 { 10 public: 11 const T& top()//top函数 12 { 13 return _con[0]; 14 } 15 16 size_t size()//size()函数 17 { 18 return _con.size(); 19 } 20 21 bool empty()//empty()函数 22 { 23 return _con.size()==0; 24 } 25 private: 26 Container _con; 27 28 }; 29 30 } ~在这里复习一个知识点,top函数能使用引用传参的条件是_con[0]出了top函数的作用域以后没有被销毁。
3.push函数
因为我们要模仿的是堆排序的模式,所以在实现push函数的同时就得实现一个向上调整建堆。向上调整建堆的代码如下:
void adjust_up(int child) 27 { 28 size_t parent = (child-1)/2; 29 while(child>0) 30 { 31 if(_con[child]<_con[parent]) 32 { 33 swap(_con[child],_con[parent]);//模板数据结构里面已经实现这个swap()函数。 34 child = parent; 35 parent = (child-1)/2; 36 } 37 else 38 { 39 break; 40 } 41 } 42 }然后在push调用的时候便是这样使用的:
void push(T& x) 45 { 46 _con.push_back(x); 47 adjust_up(_con.size()-1); 48 }当然,这段代码不能让这个堆的每个下标的大小都是符合顺序的但是可以保证这个vector类型的数组是一个堆。
4.pop函数
pop函数的实现也要依靠一个向下调整的函数。这个向下调整的函数实现代码如下:
void adjust_down(int parent) 51 { 52 int child = parent*2+1; 53 while(child<_con.size()) 54 { 55 if(child+1<_con.size()&&_con[child+1]<_con[child]) 56 { 57 child++; 58 } 59 if(_con[child]<_con[parent]) 60 { 61 swap(_con[child],_con[parent]); 62 parent = child; 63 child = parent*2+1; 64 } 65 else 66 { 67 break; 68 } 69 70 } 71 }然后我们再来实现pop()函数:
void pop() 74 { 75 swap(_con[0],_con[_con.size()-1]); 76 _con.pop_back(); 77 adjust_down(0); 78 }经过上述操作,我们的pop函数就写好了。
5.构造函数
1.迭代器构造函数:
template<class InputIterator> 36 priority_queue(InputIterator first,InputIterator last) 37 :_con(first,last) //调用模板容器的迭代器构造函数 38 { 39 for(int i=(_con.size()-1-1)/2;i>=0;i--) 40 { 41 adjust_down(i); //从最后一个父节点开始调整成堆 42 } 43 }这个迭代器区间构造函数其实是十分好写的,因为我们调用的容器里面已经实现了迭代器区间构造函数,我们复用便可以了。但是这里要注意一个点,就是在我们写下这个迭代器区间构造函数以后,默认生成的无参的构造函数就没有了。所以我们就得加一个无参的构造函数:
priority_queue() 31 { 32 33 }
6.测试
我们再创建一个.cc文件,写入以下代码:
#include"priority_queue.h" 2 3 int main() 4 { 5 area::priority_queue<int>q; 6 q.push(4); 7 q.push(3); 8 q.push(9); 9 q.push(10); 10 q.push(40); 11 q.push(99); 12 q.push(12); 13 q.push(9); 14 15 while(!q.empty()) 16 { 17 cout<<q.top()<<" "; 18 q.pop(); 19 } 20 21 cout<<endl; 22 return 0; 23 }运行结果如下:
得到这样的结果说明我们的优先级队列是写对了的。
三,仿函数
1.介绍
在上面的代码中,我们实现的是一个小堆但是如果我们要实现一个大堆呢?难道我们要改代码吗?我们当然是不用的,可以仿照qsort函数的实现手法:
在这个函数实现的时候会有一个compar函数,这个函数是函数指针类型的我们可以通过这个写这个函数的逻辑来实现按顺序排还是按逆序排。在实现优先级队列时我们也可以根据这个思想来实现相同的控制效果。但是在Cpp中是非常鄙视函数指针的。所以我们得用到一个叫做仿函数的知识。仿函数如下:
template<class T> 5 class Less 6 { 7 bool operator()(const T&x,const T&y) 8 { 9 return x<y; 10 } 11 }; 12 13 template<class T> 14 class Greater 15 { 16 bool operator()(const T&x,const T&y) 17 { 18 return x>y; 19 } 20 };这样便实现了两个仿函数了。可以看到仿函数其实不是一个函数,只不过是在一个类里面将
()重载,从而让这个类可以像函数一样使用,所以才叫做仿函数。
2.使用
实现了以上两个仿函数以后,我们便要开始在我们模拟实现的优先级队列里使用这个仿函数了。首先我们得在模板里面再添加一个模板参数compare,如下:
template<class T,class Container=vector<T>,class compare = Less<T> >并且默认生成的是小堆。然后我们再来一些替换,将比较的地方换成仿函数的对象。所以我们要先造一个仿函数对象:
compare com;然后将比较的地方替换成仿函数便可以了,如以下地方:
if(child+1<_con.size()&&com(_con[child+1],_con[child])) 78 { 79 child++; 80 } 81 if(com(_con[child],_con[parent])) 82 { 83 swap(_con[child],_con[parent]); 84 parent = child; 85 child = parent*2+1; 86 }