深度学习是机器学习领域中的一个研究方向,它被引入机器学习使其更接近于最初的目标——人工智能。
深度学习的本质其实就是一个拟合函数,通过不断的“喂入”数据(比如图片或者视频)来调节神经网络的参数,从而找到输入数据的特征范式。
深度学习的4个步骤:
①准备数据 ②搭建模型 ③迭代训练 ④使用模型
准备数据:把需要的相关数据(通常是指已经标注好的、用来训练或者教会机器模型或者算法的数据)收集起来,收集过程中需要注意训练数据的质量、多样性和数量的大小。
获得训练数据的两个方法:①通过互联网获取,网上可以找到很多免费的训练数据集。有很多科研机构把他们采集的训练数据集共享了出来。
②人为生成,如从公共数据集中手动筛选处理、打上标签,或者是通过程序编码生成。
搭建模型:深度学习的模型搭建分为两个方向:正向和反向
①正向:是指数据从输入开始,依次进行各节点定义的运算,一直运算到输出,是模型最基本的数据流向。它直观地表现了网络模型的结构,在模型的训练、测试、使用的场景中都会用到。以下为相关代码示例:
#创建模型
#声明变量
X = tf.placeholder("float")
Y = tf.placeholder("float")
#模型参数
W = tf.Variable(tf.compat.v1.random_normal([1]),name = "weight")
b = tf.Variable(tf.zeros([1]),name = "bias")
#前向结构
z = tf.multiply(X,W) + b在神经元中,W和b可以理解为两个变量。模型每次的"学习"都是调整W和b以得到一个更合适的值。最终,有这个值配合上运算公式所形成的逻辑就是神经网络的模型。
②反向:只有在训练场景下才会用到。原理是在神经网络先通过正向生成一个值后,观察其与真实值的差距,再通过反向过程将里面的参数进行调整,接着再次正向生成预测值并与真实值进行比对,这样循环下去,直到将参数调整为合适值为止。以下为反向优化的相关代码示例:
#反向优化
cost = tf.reduce_mean(tf.square(Y - z))
learning_rate = 0.01
#使用梯度下降算法
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)其中:①cost等于生成值与真实值的平方差
②learning_rate为学习率,代表调整参数的步长。这个值一般小于1,这个值越大,表明调整的步长越大,但不精准,值越小,精度越高,但速度慢
③GradientDescentOptimizer函数是一个封装好的梯度下降算法
训练模型:在TensorFlow中,通过session进行迭代训练,相关代码如下
#初始化所有变量
init = tf.global_variables_initializer()
#设置训练迭代次数
training_epochs = 20
#启动session
with tf.Session() as sess:
sess.run(init)
for epoch in range(training_epochs):
for(x,y) in zip(train_X,train_Y):
sess.run(optimizer,feed_dict={X:x,Y:y)
为了更清楚直观地了解数值信息的变化,通常使用python的matplotlib包中的pyplot库,将模型中的信息进行可视化呈现,pyplot库常用的函数主要分为两类,一类是关于图像的显示函数,一类是关于画图的函数。
使用模型
TensorFlow开发的基本步骤细分如下:
①定义TensorFlow输入节点
②定义"学习参数"的变量
③定义"运算"
④优化函数,优化目标
⑤初始化所有变量
⑥迭代更新参数到最优解
⑦测试模型
⑧使用模型
①定义TensorFlow输入节点
定义输入节点的方法主要有三种:
1.通过占位符定义,一般情况下都使用这种方式
#占位符
X = tf.placeholder("float")
Y = tf.placeholder("float")2.通过字典类型定义,一般用于输入比较多的情况
#字典占位符
inputdict = {
'X':tf.placeholder("float")
'Y':tf.placeholder("float")
}3.直接定义,即将定义好的Python变量直接放到OP节点中参与输入的运算,将模拟数据的变量直接放到模型中进行训练
#生成模拟数据
train_X = np.linspace(-1,1,100)
train_Y = 6 * train_X + np.random.randn(*train_X.shape) * 0.3②定义"学习参数"的变量
学习参数的定义与输入节点的定义类似,分为直接定义和字典定义两部分:
1.直接定义
#模型参数
W = tf.Variable(tf.random_normal([1]),name = "weight")
b = tf.Variable(tf.zeros([1]),name = "bias")2.通过字典类型定义,普遍都会使用这种
#字典方式定义模型参数
paradict = {
'W':tf.Variable(tf.random_normal([1])),
'b':tf.Variable(tf.zeros([1]))
}③定义"运算"
定义"运算"的过程是建立模型的核心过程,直接决定了模型的拟合效果。定义"运算"主要包含定义正向传播模型和定义损失函数两部分内容:
定义正向传播模型:
#前向结构
z = tf.multiply(X,W) + b上面代码例子中使用的网络结构很简单,只有一个神经元。在后面会学到多层神经网络、卷积神经网、循环神经网络及更深层的GoogleNet、Resnet等,它们都是由神经元以不同的组合方式组成的网络结构,而且每年还会有很多更高效且拟合性更强的新结构诞生。
损失函数主要是计算"输出值"与"目标值"之间的误差,是配合反向传播使用的。为了在反向传播中可以找到最小值,要求损失函数必须是可导的。如前面章节代码实例中定义的损失函数:
#损失函数
cost = tf.reduce_mean(tf.square(Y - z))④优化函数,优化目标
有了正向结构模型和损失函数后,就是通过优化函数来优化学习参数了,这个过程也是在反向传播中完成的。反向传播过程,就是沿着正向传播的结构向相反方向将误差传递过去。
⑤初始化所有变量
代码示例如下:
#初始化所有变量
init = tf.global_variables_initializer()
#启动session
with tf.Session() as sess:
sess.run(init)⑥迭代更新参数到最优解
在迭代训练环节,需要通过建立一个session来完成,常用的是使用with语法,可以在session结束后自行关闭。在session中通过run来运算模型中的节点,run里面放的是优化操作的OP,同时会在外层加上循环次数。代码示例如下:
#初始化所有变量
init = tf.global_variables_initializer()
#设置训练迭代次数
training_epochs = 20
#启动session
with tf.Session() as sess:
sess.run(init)
for epoch in range(training_epochs):
for(x,y) in zip(train_X,train_Y):
sess.run(optimizer,feed_dict = {X:x,Y:y})以下是示例完整代码:
# -*- coding: utf-8 -*-
"""
Created on
@author:
"""
import tensorflow.compat.v1 as tf
import numpy as np
import matplotlib.pyplot as plt
tf.compat.v1.disable_eager_execution()#这个函数用于禁用 TensorFlow 2 中的即时执行模式,以便能够使用 TensorFlow 1.x 的计算图执行方式。
#1.准备数据
train_X = np.linspace(-1, 1,100)#train_X 是一个从 -1 到 1 的等间距数组,用作输入特征。
train_Y = 5 * train_X + np.random.randn(*train_X.shape) * 0.7#train_Y 是根据 train_X 生成的目标值,在真实值的基础上加上了一些噪声。
#2.搭建模型
#通过占位符定义
X = tf.placeholder("float")#X 和 Y 是 TensorFlow 的占位符(Placeholder),用于在执行时提供输入和标签数据。
Y = tf.placeholder("float")
#定义学习参数的变量
W = tf.Variable(tf.compat.v1.random_normal([1]),name="weight")#W 和 b 是学习参数的变量,可以被模型训练调整。
b = tf.Variable(tf.zeros([1]),name="bias")
#定义运算
z = tf.multiply(X,W) + b#z 是通过将输入特征 X 与权重 W 相乘并加上偏差 b 得到的预测值。
#定义损失函数
cost = tf.reduce_mean(tf.square(Y - z))#cost 是损失函数,计算预测值与真实值之间的平方差的平均值。
#定义学习率
learning_rate = 0.01#learning_rate 是学习率,用来控制优化算法在每次迭代中更新参数的步长。
#设置优化函数
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)#optimizer 是梯度下降优化器,用于最小化损失函数。
#3.迭代训练
#初始化所有变量
init = tf.global_variables_initializer()
#定义迭代参数
training_epochs = 20#training_epochs 是迭代训练的轮数。
display_step = 2#display_step 是控制训练过程中打印输出的步长。
#启动Session
with tf.Session() as sess:#with tf.Session() as sess: 创建一个会话,在该会话中执行计算图操作。
sess.run(init)#sess.run(init) 运行初始化操作,初始化所有变量。
for epoch in range(training_epochs):
for(x,y) in zip(train_X,train_Y):
sess.run(optimizer,feed_dict={X:x,Y:y})#sess.run(optimizer,feed_dict={X:x,Y:y}) 执行一次优化器操作,将当前的输入特征 x 和标签值 y 传入模型。
if epoch % display_step == 0:#每隔 display_step 轮迭代打印一次损失值和当前的参数值。
loss=sess.run(cost,feed_dict={X:train_X,Y:train_Y})
#测试模型
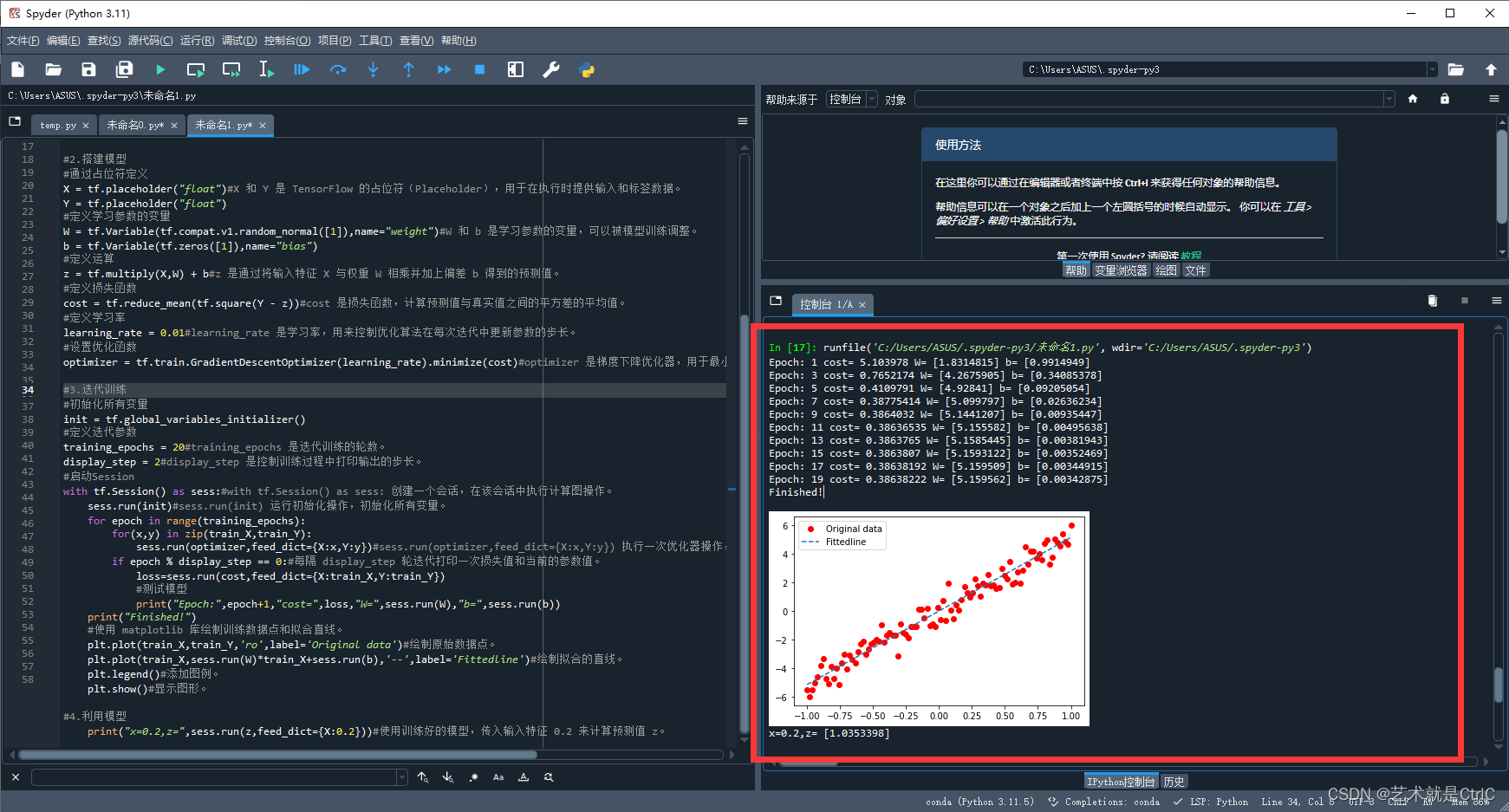
print("Epoch:",epoch+1,"cost=",loss,"W=",sess.run(W),"b=",sess.run(b))
print("Finished!")
#使用 matplotlib 库绘制训练数据点和拟合直线。
plt.plot(train_X,train_Y,'ro',label='Original data')#绘制原始数据点。
plt.plot(train_X,sess.run(W)*train_X+sess.run(b),'--',label='Fittedline')#绘制拟合的直线。
plt.legend()#添加图例。
plt.show()#显示图形。
#4.利用模型
print("x=0.2,z=",sess.run(z,feed_dict={X:0.2}))#使用训练好的模型,传入输入特征 0.2 来计算预测值 z。运行效果如下: