💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
摆动曲线参数的优化在电力系统稳定性分析中至关重要。有效调整参数有助于确保系统在故障发生后保持稳定,并防止潜在的灾难性后果。然而,确定最佳参数值一直是一个具有挑战性的任务。为了解决这个问题,粒子群优化(PSO)算法被引入,为工程师和研究人员提供了一种有效的优化技术。
本文使用PSO算法来优化摆动曲线仿真的参数。PSO算法旨在找到最佳参数集,以在指定时间内实现所需的转子角度。具体而言,该脚本基于预定义的模型对摆动曲线进行了模拟,并通过迭代更新粒子的位置和速度来逐步收敛到最优解。通过这种方式,PSO算法能够搜索参数空间中的最佳组合,以实现稳定的电网。
一旦获得了优化的参数,我们可以使用它们来生成摆动曲线,并展示转子角度随时间的变化。这些曲线可以帮助工程师和研究人员更好地理解系统的稳定性,并为他们提供准确的参考,以便在实际运行中采取必要的措施。
通过使用PSO算法进行摆动曲线参数优化,我们能够提高电力系统稳定性分析的准确性和效率。这种优化技术为我们提供了一种快速而可靠的方法,以确保电网在故障情况下保持稳定,并最大程度地减少潜在的灾难性后果。因此,PSO算法在电力系统稳定性分析中具有重要的应用价值。
📚2 运行结果
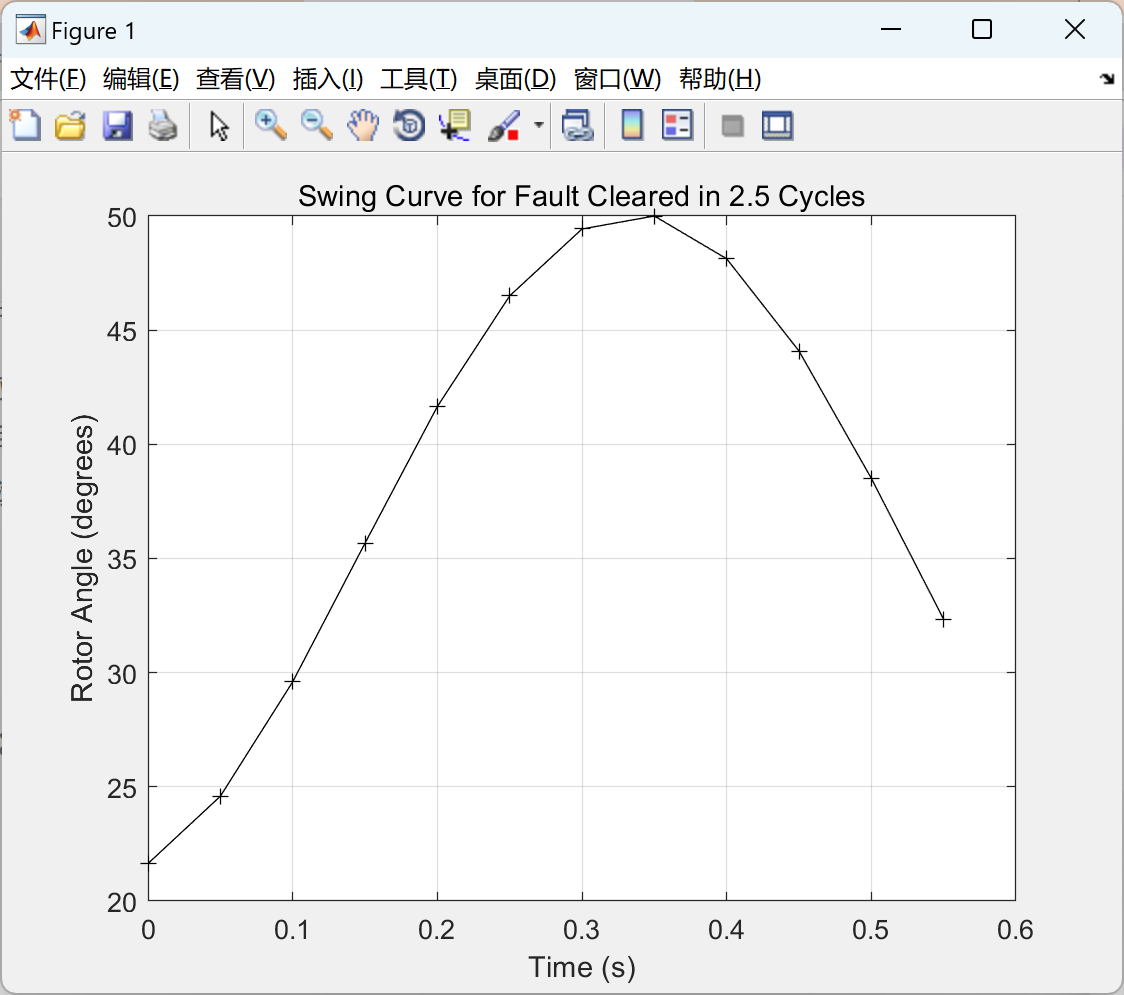
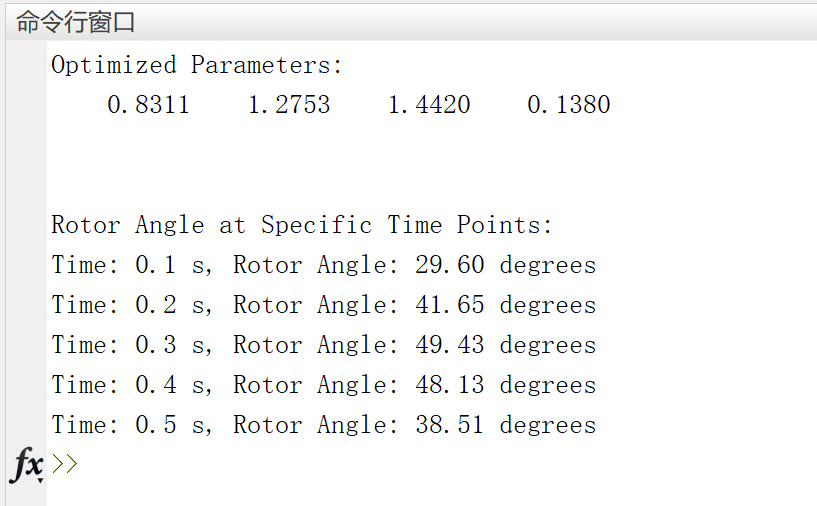
部分代码:
% Plot the swing curve
figure;
plot(time, ang, 'k+-')
title('Swing Curve for Fault Cleared in 2.5 Cycles');
xlabel('Time (s)');
ylabel('Rotor Angle (degrees)');
grid on;
% Display rotor angle values at specific time points
display_time_points = [0.1, 0.2, 0.3, 0.4, 0.5]; % Add more time points as needed
displayed_angles = interp1(time, ang, display_time_points);
fprintf('\nRotor Angle at Specific Time Points:\n');
for i = 1:numel(display_time_points)
fprintf('Time: %.1f s, Rotor Angle: %.2f degrees\n', display_time_points(i), displayed_angles(i));
end
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]徐倩,康积涛,王德林,等.基于PSO算法的IEEEACSA励磁系统对电力系统电压稳定性的影响[J].电工技术, 2016(8):3.
[2]周敏.基于PSO算法的电力系统稳定器参数优化[J].重庆电力高等专科学校学报, 2010(003):015.
[3]卢岑岑吴跨宇王晓茹.基于PSO算法的直流有功功率调制参数优化研究[J].浙江电力, 2016, 000(001):1-5.