前面做出了一个比较好的里程计，但是在实际项目使用的时候，都是基于地图的。原因如下：

1. 基于地图有先验的信息，地图的质量是经过检查了的，它没有太多的不可控在里面。而里程计有很多的干扰因素在里面，会导致里程计的不稳定。
2. 地图更多是一个全局优化得到的结果，误差相比于里程计会更小。

建图流程如下：

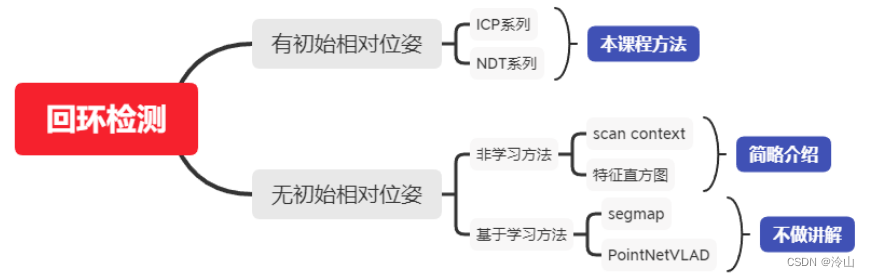
1. 回环检测

• 目的：消除累计误差，并提高地图一致性。
• 方法：从历史帧中找出相似帧（即物理世界中相近位置且有充足共视区域的帧），并给出二者的相对位姿。(注意，不需要完全重合)
• 用法：在后端优化中，作为一个相对位姿约束的边，加入图优化系统中。

目前比较可靠的方法还是ICP和NDT两个比较基础的方法（小范围可以使用里程计确定是不是在之前帧周边，大范围就需要用到GPS了）。

1.1 基于Scan Context

论文：Scan Context: Egocentric Spatial Descriptor for Place Recognition within 3D Point Cloud Map

基本思想为，将一圈点云分成很多的扇形，每个扇形在纵向上再切割成小段。三维点云展开，就成了二维数组。下次再走到这里的时候，根据二维数组的匹配相似性，就能判断是不是同一区域了。
缺点：旋转可以计算，但是平移计算不准。

应用案例： LeGO-LOAM + scan context 闭环检测

1.2 基于直方图

论文：[A fast, complete, point cloud based loop closure for LiDAR odometry and mapping]
应用案例：loam_livox

将点云按三维网格划分，每个网格求特征值，会有三个特征值。如果将每帧点云跟之前帧匹配计算相似性，可以大致判断出来是不是走到了同一位置。

2. 后端优化

2.1 后端优化基本原理

目的：利用 回环检测结果 和 惯导先验位姿 修正里程计误差，得到一个高质量的地图。回环在此处提供的是两帧之间的相对位姿。
观测：

1. 连续两帧的相对位姿观测；
2. 回环匹配得到的相对位姿观测；
3. 组合导航提供的先验位姿观测。

使用方式：
a. 1)和2)的观测构成了基于回环的位姿修正(LeGO-LOAM)；
b. 1)和3)的观测构成了基于先验观测的位姿修正；
c. 1) 2) 3) 也可以同时使用。

2.2 李群、李代数基本知识

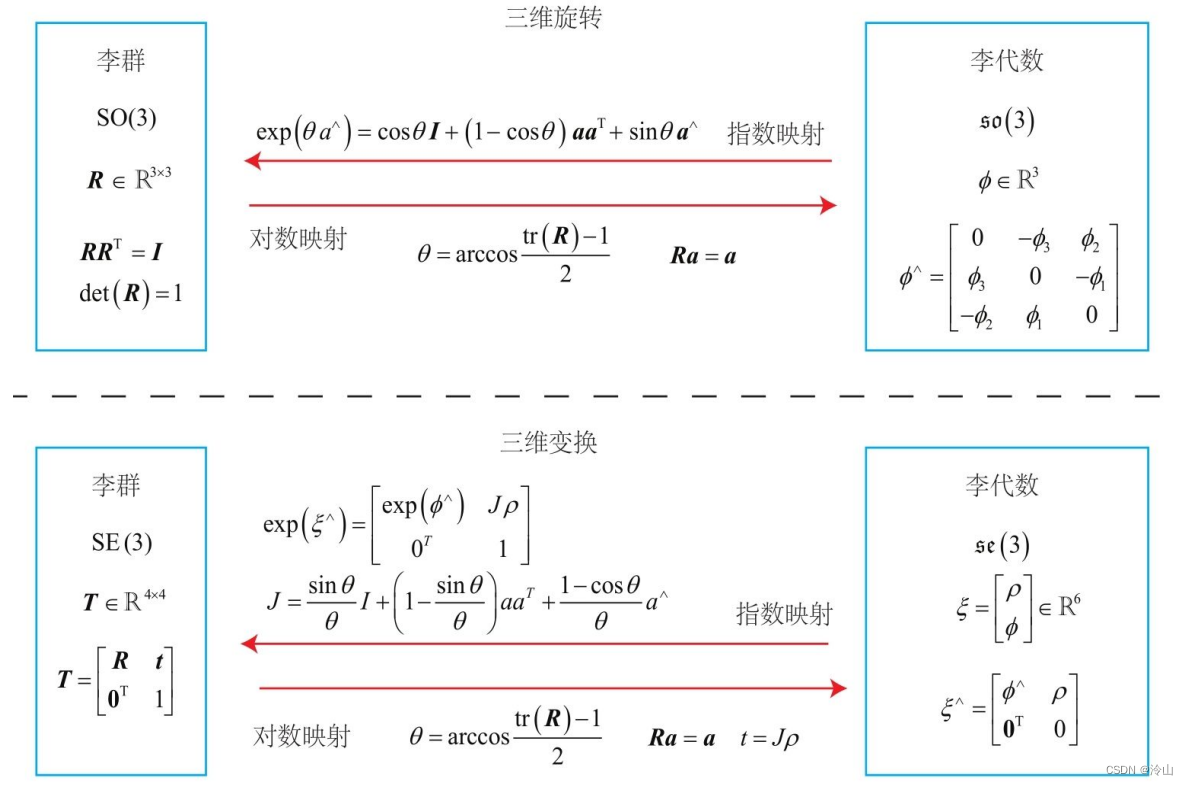
常用转换：

• $R=\exp \left({\mathbf{\varphi }}^{\wedge }\right)$
  $R^{-1}=\exp \left((-\mathbf{\varphi }{)}^{\wedge }\right)$
  $\mathbf{\varphi }=\ln {\left(\exp \left({\mathbf{\varphi }}^{\wedge }\right)\right)}^{\vee }=\ln (R{)}^{\vee }$
• $T=\exp \left({\mathbf{\xi }}^{\wedge }\right)$
  $T^{-1}=\exp \left((-\mathbf{\xi }{)}^{\wedge }\right)$
  $\mathbf{\xi }=\ln {\left(\exp \left({\mathbf{\xi }}^{\wedge }\right)\right)}^{\vee }=\ln (T{)}^{\vee }$

2.3 李群、李代数基本知识

在推导里永远无法避免使用 BCH 公式：
$$\ln (\exp (A)\exp (B))=A+B+\frac{1}{2}[A,B]+\frac{1}{12}[A,[A,B]]-\frac{1}{12}[B,[A,B]]+\cdots$$这个公式用来解决一个问题：
已知 $T=T_1\cdot T_2$，又知道 $T=\exp \left({\mathbf{\xi }}^{\wedge }\right)$，那么 $\exp \left({{\mathbf{\xi }}_1}^{\wedge }\right)\exp \left({{\mathbf{\xi }}_2}^{\wedge }\right)$ 这两项相乘能得到什么呢，或者说，这个 $T$ 所对应的李代数，是什么呢？

BCH公式，就是解决的这个问题。这里公式中使用$A$和$B$，是因为这两下既可能是在so(3)下的表达，又可能是在$se(3)$下的表达。这里使用 $\ln (\exp (A)\exp (B))$，就是求它对应的李代数。可以看出来，公式不是只有$A+B$，而是多了后面的几项。

• $\mathrm{SO}(3)$ 下的李括号定义为：
  $$\left[{\mathbf{\varphi }}_1,{\mathbf{\varphi }}_2\right]={\left({\Phi }_1{\Phi }_2-{\Phi }_2{\Phi }_1\right)}^{\vee }$$其中，
  $$\Phi ={\varphi }^{\wedge }=\left[\begin{array}{ccc}0& -\varphi (3)& \varphi (2)\\ \varphi (3)& 0& -\varphi (1)\\ -\varphi (2)& \varphi (1)& 0\end{array}\right]$$

• $\mathrm{SE}(3)$ 下的李括号定义为：
  $$\left[{\mathbf{\xi }}_1,{\mathbf{\xi }}_2\right]={\left({\mathbf{\xi }}_1^{\wedge }{\mathbf{\xi }}_2^{\wedge }-{\mathbf{\xi }}_2^{\wedge }{\mathbf{\xi }}_1^{\wedge }\right)}^{\vee }$$

但是很显然，这个BCH公式太复杂了，那么我们有没有简化的方式来解决它呢？这里根据 so(3) 和 se(3)，给出了两个简化的表达。

2.3.1 $\mathrm{SO}(3)$ 对应的 $\mathrm{BCH}$ 公式

(小量可以想像成，第$k$帧和第$k+1$帧的相对旋转，而另一个即为坐标系下当前角度)
$$\ln {\left(\exp \left({\mathbf{\varphi }}_1^{\wedge }\right)\exp \left({\varphi }_2^{\wedge }\right)\right)}^{\vee }\approx \{\begin{array}{l}{J}_l{\left({\mathbf{\varphi }}_2\right)}^{-1}{\mathbf{\varphi }}_1+{\mathbf{\varphi }}_2\text{, 当 }{\mathbf{\varphi }}_1\text{ 为小量 }\\ J_r{\left({\mathbf{\varphi }}_1\right)}^{-1}{\mathbf{\varphi }}_2+{\mathbf{\varphi }}_1\text{, 当 }{\mathbf{\varphi }}_2\text{ 为小量 }\end{array}$$其中左乘雅可比为：(左乘意味着在左边乘上一个小旋转)
$$J_l=\frac{\sin \theta }{\theta }I+\left(1-\frac{\sin \theta }{\theta }\right)a{a}^{\mathrm{T}}+\frac{1-\cos \theta }{\theta }{a}^{\wedge }$$即：
$$J_l^{-1}=\frac{\theta }{2}\cot \frac{\theta }{2}I+\left(1-\frac{\theta }{2}\cot \frac{\theta }{2}\right)a{a}^T-\frac{\theta }{2}{a}^{\wedge }$$右乘雅可比仅需要在左乘雅可比的基础上对自变量取负号，即：
$$J_r(\mathbf{\varphi })=J_l(-\mathbf{\varphi })$$

2.3.2 $\mathrm{SE}(3)$ 对应的 $\mathrm{BCH}$ 公式

$$\ln {\left(\exp \left({\mathbf{\xi }}_1^{\wedge }\right)\exp \left({\mathbf{\xi }}_2^{\wedge }\right)\right)}^{\vee }\approx \{\begin{array}{l}{\mathcal{J}}_{\ell }{\left({\mathbf{\xi }}_2\right)}^{-1}{\mathbf{\xi }}_1+{\mathbf{\xi }}_2\text{ ，当 }{\mathbf{\xi }}_1\text{ 为小量 }\\ {\mathcal{J}}_r{\left({\mathbf{\xi }}_1\right)}^{-1}{\mathbf{\xi }}_2+{\mathbf{\xi }}_1\text{ ，当 }{\mathbf{\xi }}_2\text{ 为小量 }\end{array}$$由于SE(3)上的雅可比形式过于复杂，此处直接给出本章所用到的近似形式如下。详细内容可参考《机器人中的状态估计》 中公式7.83的推导过程。($J_l$更复杂)
$${\mathcal{J}}_r(\mathbf{\xi }{)}^{-1}\approx I+\frac{1}{2}\left[\begin{array}{cc}{\mathbf{\varphi }}^{\wedge }& {\mathbf{\rho }}^{\wedge }\\ 0& {\mathbf{\varphi }}^{\wedge }\end{array}\right]$$若 ${\mathbf{\xi }}_1$ 和 ${\mathbf{\xi }}_2$ 非常小，则左右雅可比均可以直接约等于单位阵，即${\mathcal{J}}_r(\mathbf{\xi }{)}^{-1}\approx I$，此时有
$$\exp \left({\mathbf{\xi }}_1^{\wedge }\right)\exp {\left({\mathbf{\xi }}_2^{\wedge }\right)}^{\vee }\approx \exp {\left({\mathbf{\xi }}_1^{\wedge }+{\mathbf{\xi }}_1^{\wedge }\right)}^{\vee }$$

2.4 伴随矩阵

$\mathrm{SO}(3)$ 上的伴随性质：
$$\exp \left(p^{\wedge }\right)R=R\exp \left({\left(R^{-1}p\right)}^{\wedge }\right)$$$SE(3)$ 上的伴随性质：
$$\exp \left({\xi }^{\wedge }\right)T=T\exp \left({\left(\mathrm{Ad}\left(T^{-1}\right)\xi \right)}^{\wedge }\right)$$其中伴随矩阵的定义如下：
$$\mathrm{Ad}(T)=\left[\begin{array}{cc}R& t^{\wedge }R\\ 0& R\end{array}\right]$$

伴随矩阵的目的是，假设我们有$\exp \left(p^{\wedge }\right)R$，想对$p$求偏导，但是$p$在左边是很难求偏导的，转到右边之后，偏导就比较容易求了。

2.3 基于回环的位姿修正

位姿图优化是把所有的观测和状态放在一起优化，残差项是前面所讲的残差项的总和。在实际使用中，各残差会被分配一个权重，也就是信息矩阵，它相当于对残差进行加权。考虑信息矩阵后，总的残差项可以表示为：$\mathbf{F}(\mathbf{x})={\sum }_{⟨i,j⟩\in \mathcal{C}}\underset{{\mathbf{F}}_{ij}}{\underbrace{{\mathbf{e}}_{ij}^T{\mathbf{\Omega }}_{ij}{\mathbf{e}}_{ij}}}$

此时优化问题可以表示为：${\mathbf{x}}^{\ast }=\underset{\mathbf{x}}{\mathrm{argmin}}\mathbf{F}(\mathbf{x})$

第 $\mathrm{i}$ 帧和第 $\mathrm{j}$ 帧之间的相对位姿，在李群SE(3)上可以表示为：${\mathbf{T}}_{ij}={\mathbf{T}}_i^{-1}{\mathbf{T}}_j$
也可以在李代数上表示为：
$$\begin{array}{rl}{\mathbf{\xi }}_{ij}& =\ln {\left({\mathbf{T}}_i^{-1}{\mathbf{T}}_j\right)}^{\vee }\\ & =\ln {\left(\exp \left({\left(-{\mathbf{\xi }}_i\right)}^{\wedge }\right)\exp \left({\mathbf{\xi }}_j^{\wedge }\right)\right)}^{\vee }\end{array}$$若位姿没有误差，则上面两个式子是精确相等的，但当位姿有误差存在时，便可以使用等式的左右两端计算残差项。(也就是，第 $\mathrm{i}$ 帧和第 $\mathrm{j}$ 帧之间的相对位姿，要添加一个什么样的转换才能到$T_{ij}$，要是相等，这里就是一个单位阵$I$)
$$\begin{array}{rl}{\mathbf{e}}_{ij}& =\ln {\left({\mathbf{T}}_{ij}^{-1}{\mathbf{T}}_i^{-1}{\mathbf{T}}_j\right)}^{\vee }\\ & =\ln {\left(\exp \left({\left(-{\mathbf{\xi }}_{ij}\right)}^{\wedge }\right)\exp \left({\left(-{\mathbf{\xi }}_i\right)}^{\wedge }\right)\exp \left({\mathbf{\xi }}_j^{\wedge }\right)\right)}^{\vee }\end{array}$$位姿图优化的思想是通过调整状态量(即位姿)，使残差项的值最小化，这就需要用残差项对位姿求雅可比，才能使用高斯牛顿方法进行优化。(需要对矩阵求导了)

求雅可比的方式是对位姿添加扰动，此时残差表示为：
$${\hat{\mathbf{e}}}_{ij}=\ln {\left({\mathbf{T}}_{ij}^{-1}{\mathbf{T}}_i^{-1}\exp \left({\left(-\mathbf{\delta }{\mathbf{\xi }}_i\right)}^{\wedge }\right)\exp \left(\delta {\mathbf{\xi }}_j^{\wedge }\right){\mathbf{T}}_j\right)}^{\vee }$$这里的扰动都是左扰动，${\mathbf{T}}_j$ 的扰动是 $\exp \left(\delta {\mathbf{\xi }}_j^{\wedge }\right)$，而${\mathbf{T}}_i$的在右边是因为这里是求的它的逆。

进一步对前面的式子进行化简：
$$\begin{array}{rl}{\hat{e}}_{ij}& =\ln {\left({\mathbf{T}}_{ij}^{-1}{\mathbf{T}}_i^{-1}\exp \left({\left(-\delta {\mathbf{\xi }}_i\right)}^{\wedge }\right)\exp \left(\delta {\mathbf{\xi }}_j^{\wedge }\right){\mathbf{T}}_j\right)}^{\vee }\\ & \stackrel{(1)}{=}\ln ({\mathbf{T}}_{ij}^{-1}{\mathbf{T}}_i^{-1}\exp \left({\left(-\delta {\mathbf{\xi }}_i\right)}^{\wedge }\right){\mathbf{T}}_j\exp {\left({\left(\mathrm{Ad}\left({\mathbf{T}}_j^{-1}\right)\delta {\mathbf{\xi }}_j\right)}^{\wedge }\right)}^{\vee }\\ & \stackrel{(2)}{=}\ln ({\mathbf{T}}_{ij}^{-1}{\mathbf{T}}_i^{-1}{\mathbf{T}}_j\exp \left({\left(-\mathrm{Ad}\left({\mathbf{T}}_j^{-1}\right)\delta {\mathbf{\xi }}_i\right)}^{\wedge }\right)\exp {\left({\left(\mathrm{Ad}\left({\mathbf{T}}_j^{-1}\right)\mathbf{\delta }{\mathbf{\xi }}_j\right)}^{\wedge }\right)}^{\vee }\\ & \stackrel{(3)}{\approx }\ln ({\mathbf{T}}_{ij}^{-1}{\mathbf{T}}_i^{-1}{\mathbf{T}}_j\exp {\left({\left(-\mathrm{Ad}\left({\mathbf{T}}_j^{-1}\right)\delta {\mathbf{\xi }}_i\right)}^{\wedge }+{\left(\mathrm{Ad}\left({\mathbf{T}}_j^{-1}\right)\delta {\mathbf{\xi }}_j\right)}^{\wedge }\right)}^{\vee }\\ & \stackrel{(4)}{=}\ln (\exp \left({\mathbf{e}}_{ij}^{\wedge }\right)\exp {\left({\left(-\mathrm{Ad}\left({\mathbf{T}}_j^{-1}\right)\delta {\mathbf{\xi }}_i\right)}^{\wedge }+{\left(\mathrm{Ad}\left({\mathbf{T}}_j^{-1}\right)\delta {\mathbf{\xi }}_j\right)}^{\wedge }\right)}^{\vee }\\ & \stackrel{(5)}{\approx }{\mathbf{e}}_{ij}-{\mathcal{J}}_r^{-1}\left(e_{ij}\right)\mathrm{Ad}\left({\mathbf{T}}_j^{-1}\right)\delta {\mathbf{\xi }}_i+{\mathcal{J}}_r^{-1}\left(e_{ij}\right)\mathrm{Ad}\left({\mathbf{T}}_j^{-1}\right)\mathbf{\delta }{\mathbf{\xi }}_j\end{array}$$

首先要将两个exp放到最右边去：
(1) 三维变换下的伴随性质，先将 $\exp \left(\delta {\mathbf{\xi }}_j^{\wedge }\right)$ 移到右边去；
(2) 三维变换下的伴随性质，这次是将 $\exp \left(\delta {\mathbf{\xi }}_i^{\wedge }\right)$ 移到右边去；
(3) $\mathrm{BCH}$ 公式，且是两个李代数都比较小情况下的近似。就是两个李代数对应都非常小的时候，可以使用$\exp \left({\mathbf{\xi }}_1^{\wedge }\right)\exp {\left({\mathbf{\xi }}_2^{\wedge }\right)}^{\vee }\approx \exp {\left({\mathbf{\xi }}_1^{\wedge }+{\mathbf{\xi }}_1^{\wedge }\right)}^{\vee }$的形式。
(4) 残差的定义，即 ${\mathbf{e}}_{ij}=\ln {\left({\mathbf{T}}_{ij}^{-1}{\mathbf{T}}_i^{-1}{\mathbf{T}}_j\right)}^{\vee }$
(5) BCH 公式

上面的式子表明，残差关于 $T_i$ 的雅可比为：
$$A_{ij}=\frac{\partial {\mathbf{e}}_{ij}}{\partial \mathbf{\delta }{\mathbf{\xi }}_i}=-{\mathcal{J}}_r^{-1}\left({\mathbf{e}}_{ij}\right)\mathrm{Ad}\left({\mathbf{T}}_j^{-1}\right)$$残差关于 $T_j$ 的雅可比为：
$$B_{ij}=\frac{\partial {\mathbf{e}}_{ij}}{\partial \mathbf{\delta }{\mathbf{\xi }}_j}={\mathcal{J}}_r^{-1}\left({\mathbf{e}}_{ij}\right)\mathrm{Ad}\left({\mathbf{T}}_j^{-1}\right)$$其中：
$${\mathcal{J}}_r^{-1}\left({\mathbf{e}}_{ij}\right)\approx I+\frac{1}{2}\left[\begin{array}{cc}{\mathbf{\varphi }}_e^{\wedge }& {\mathbf{\rho }}_e^{\wedge }\\ 0& {\mathbf{\varphi }}_e^{\wedge }\end{array}\right]$$

现在有了雅克比了，剩下的就是高斯牛顿的流程了。
按照高斯牛顿法的流程，需要对残差进行一阶泰勒展开， 即求雅可比：
$$\begin{array}{l}{\mathbf{e}}_{ij}\left({\mathbf{x}}_i+\Delta {\mathbf{x}}_i,{\mathbf{x}}_j+\Delta {\mathbf{x}}_j\right)\\ ={\mathbf{e}}_{ij}(\mathbf{x}+\Delta \mathbf{x})\\ \approx {\mathbf{e}}_{ij}+{\mathbf{J}}_{ij}\Delta \mathbf{x}\end{array}$$
其中 ${\mathbf{J}}_{ij}$ 即为前面推导的残差关于位姿的雅可比组成的矩阵：
$${\mathbf{J}}_{ij}=(0\cdots 0\underset{\text{node }i}{\underbrace{{\mathbf{A}}_{ij}}}0\cdots 0\underset{\text{node }j}{\underbrace{{\mathbf{B}}_{ij}}}0\cdots 0)$$对于每一个残差块，便有：
$$\begin{array}{l}{\mathbf{F}}_{ij}(\mathbf{x}+\Delta \mathbf{x})\\ ={\mathbf{e}}_{ij}(\mathbf{x}+\Delta \mathbf{x}{)}^T{\Omega }_{ij}{\mathbf{e}}_{ij}(\mathbf{x}+\Delta \mathbf{x})\\ \approx {\left({\mathbf{e}}_{ij}+{\mathbf{J}}_{ij}\Delta \mathbf{x}\right)}^T{\Omega }_{ij}\left({\mathbf{e}}_{ij}+{\mathbf{J}}_{ij}\Delta \mathbf{x}\right)\\ =\underset{c_{ij}}{\underbrace{{\mathbf{e}}_{ij}^T{\Omega }_{ij}{\mathbf{e}}_{ij}}}+2\underset{{\mathbf{b}}_{ij}^T}{\underbrace{{\mathbf{e}}_{ij}^T{\Omega }_{ij}{\mathbf{J}}_{ij}}}\Delta \mathbf{x}+\Delta {\mathbf{x}}^T\underset{{\mathbf{H}}_{ij}}{\underbrace{{\mathbf{J}}_{ij}^T{\Omega }_{ij}{\mathbf{J}}_{ij}}}\Delta \mathbf{x}\\ =c_{ij}+2{\mathbf{b}}_{ij}^T\Delta \mathbf{x}+\Delta {\mathbf{x}}^T{\mathbf{H}}_{ij}\Delta \mathbf{x}\end{array}$$其中：
$${\mathbf{H}}_{ij}=\left(\begin{array}{cccc}\ddots & & & \\ & {\mathbf{A}}_{ij}^T{\Omega }_{ij}{\mathrm{A}}_{ij}& \cdots & {\mathbf{A}}_{ij}^T{\Omega }_{ij}{\mathrm{B}}_{ij}\\ ⋮& \ddots & ⋮& \\ & {\mathrm{B}}_{ij}^T{\Omega }_{ij}{\mathrm{A}}_{ij}& \cdots & {\mathrm{B}}_{ij}^T{\Omega }_{ij}{\mathrm{B}}_{ij}\\ \ddots & & & \end{array}\right){\mathrm{b}}_{ij}=\left(\begin{array}{c}⋮\\ {\mathrm{A}}_{ij}^T{\Omega }_{ij}{\mathrm{e}}_{ij}\\ ⋮\\ {\mathrm{B}}_{ij}^T{\Omega }_{ij}{\mathrm{e}}_{ij}\\ ⋮\end{array}\right)$$
此后便可以使用高斯牛顿法进行优化。

2.4 基于先验观测的位姿修正

先验观测是一元边，它不像前面所述的帧间观测连接两个 位姿状态，而是只连接一个位姿状态量，它直接给出的就 是该状态量的观测值，因此它对应的残差就是观测值与状 态量之间的差异，即
$$\begin{array}{rl}{\mathbf{e}}_i& =\ln {\left({\mathbf{Z}}_i^{-1}{\mathbf{T}}_i\right)}^{\vee }\\ & =\ln {\left(\exp \left({\left(-{\mathbf{\xi }}_{zi}\right)}^{\wedge }\right)\exp \left({\mathbf{\xi }}_i^{\wedge }\right)\right)}^{\vee }\end{array}$$
对残差添加扰动，可得
$${\hat{\mathbf{e}}}_i=\ln {\left({\mathbf{Z}}_i^{-1}\exp \left(\delta {\mathbf{\xi }}_i^{\wedge }\right){\mathbf{T}}_i\right)}^{\vee }$$
利用伴随性质和 $\mathrm{BCH}$ 公式进行化简，可得
$$\begin{array}{rl}{\hat{\mathbf{e}}}_i& =\ln {\left({\mathbf{Z}}_i^{-1}{\mathbf{T}}_i\exp \left({\left(\mathrm{Ad}\left({\mathbf{T}}_i^{-1}\right)\delta {\mathbf{\xi }}_i\right)}^{\wedge }\right)\right)}^{\vee }\\ & =\ln {\left(\exp \left({\mathbf{e}}_i^{\wedge }\right)\exp \left({\left(\mathrm{Ad}\left({\mathbf{T}}_i^{-1}\right)\delta {\mathbf{\xi }}_i\right)}^{\wedge }\right)\right)}^{\vee }\\ & \approx e_i+{\mathcal{J}}_r^{-1}\left({\mathbf{e}}_i\right)\mathrm{Ad}\left({\mathbf{T}}_i^{-1}\right)\delta {\mathbf{\xi }}_i\end{array}$$因此残差关于 $T_i$ 的雅可比为
$$\frac{\partial {\mathbf{e}}_i}{\partial \mathbf{\delta }{\mathbf{\xi }}_i}={\mathcal{J}}_r^{-1}\left({\mathbf{e}}_i\right)\mathrm{Ad}\left({\mathbf{T}}_i^{-1}\right)$$其中：
$${\mathcal{J}}_r^{-1}\left(e_i\right)\approx I+\frac{1}{2}\left[\begin{array}{cc}{\varphi }_e^{\wedge }& {\mathbf{\rho }}_e^{\wedge }\\ 0& {\varphi }_e^{\wedge }\end{array}\right]$$后面的推导过程，便与相对位姿做观测的推导过程完全一致。

此外，部分场合提供的观测只有位置，没有姿态，比如只 有RTK，而没有组合导航，这里的残差便只剩下位置误差。 相应的雅可比公式，可自行推导。

3. 点云地图建立

3.1 整体流程

建图流程设计的核心原则是准确、高效地把里程计相对位姿、回环相对位姿、惯导先验位姿进行融合。

轨迹对齐：比如有个GPS轨迹和一个激光里程计，两个轨迹没有在一起，是因为初始的激光里程计是以单位阵为原点的，它与GPS之间没有产生过任何相对位姿联系。解决这个问题的方法是，把整个轨迹做调整，把激光里程计的轨迹旋转到GPS轨迹附近。
添加先验约束：如果没有检测到回环，需要添加GPS的先验位姿

4. 基于地图的定位

4.1 整体流程

在地图匹配中，鲁棒性和运行速度更加重要，因此实际使用中，基于NDT的匹配使用更广泛。

获取初始信息：假如有一个地图，这个地图很大，有可能在任何位置，需要有一个东西告诉你你在地图的哪个大致位置，如有GPS告诉我在一个位置，这时就需要把这附近一块区域的地图索引出来，索引出来后将当前雷达的点云和地图做匹配。为什么叫索引呢？因为不索引的话，就需要和整张地图做匹配了，这时不现实的，所以需要和局部地图做匹配，因此就加载一小块局部地图。

位姿初始化：在正式匹配之前，需要做一个初始化。第一次匹配前，需要多这么一个步骤。后面再做匹配时，就不需要这样做了，因为有了上一帧的位姿做参考。

更新局部地图：在地图上肯定是要沿着轨迹走的，上次加载的局部地图在一个位置，走到后面时，跟前面的局部地图就匹配不上了，因此需要拿另一块局部地图来做匹配。

4.2 位姿初始化

4.2.1 整体流程

由于NDT匹配需要较准确的初始位姿，因此在定位之前需要初始化环节，给出载体的初始位姿。
按照难度由低到高，常见的初始化需求有这样几种：

1. 已知位姿的初始化
   2）位置已知而姿态位置的初始化
   3）位置和姿态均未知的初始化

4.2.2 位姿初始化

由于NDT匹配需要较准确的初始位姿，因此在定位之前需要初始化环节，给出载体的初始位姿。

按照难度由低到高，常见的初始化需求有这样几种：
1）已知位姿的初始化
2）位置已知而姿态位置的初始化
3）位置和姿态均未知的初始化(非常有难度)

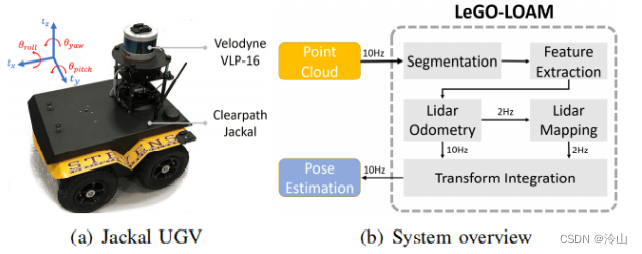
5. LeGO-LOAM介绍

论文：LeGO-LOAM: Lightweight and Ground-Optimized Lidar Odometry and Mapping on Variable Terrain

5.1 主要特点

1. 对地面做了分割，减小了特征搜索范围(环境中找线特征，地面找面特征)；
2. 提取特征之前做了聚类，提高了特征质量(很多曲率大的地方都是杂点，甚至树叶上的点都当成线特征来使用了)，这里删除掉了环境中比较杂乱的点，即不形成足够数量的点；
3. 以帧为单位进行优化，使得全局地图可以多次调整，而不像LOAM那样不可修改；
4. 增加了回环修正。

5.2 特征提取

1. 根据线与线之间的夹角，以及点的曲率，筛选出地面点。所有用于匹配的平面点仅使用地面点。
2. 在非地面点中，使用广度优先搜索(BFS)做聚类，聚类中点的数量大于30，才用来筛选线特征。
3. 筛选线特征方法，与LOAM中相同。

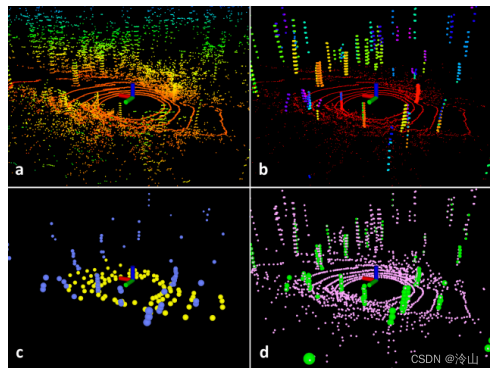
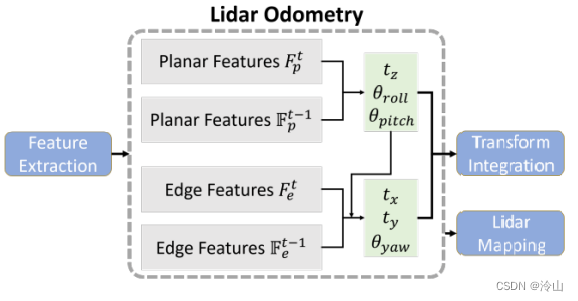
5.3 位姿解算

LeGO-LOAM 相较于之前的 LOAM 有个很重要的区别，它把6dof拆成了两个3dof。从理论上讲，面特征既然都提自于地面，那么它确实只能约束两个水平角和z向的距离；线特征也一样，它不在地面只分配在周围，而且大多数线特征都是竖直向上的，那它也确实只能约束航向角以及x、y的距离。这个理论上，从6dof拆成3dof和周围环境结合起来分析，它在精度上是没有损失的（或者说损失较少？），但是效率上会大幅提升。

1. 使用地面面特征优化高度和水平角；
2. 使用线特征优化水平位移和航向角。

注意：实际代码中，只有odom环节(scan-to-scan)使用了该模式，在mapping环节(scan-to-map)仍使用的是六自由度模型。

5.4 回环检测与修正

1. 回环检测使用的初始位姿，采用前端里程计位姿
2. 匹配采用 ICP 方法
3. 优化库采用 gtsam