题目

思路

对于限制2，可以发现，如果 $i$ 不选，那么 $i-1$ 和 $i+1$ 就一定要选，2-SAT可以很好地解决

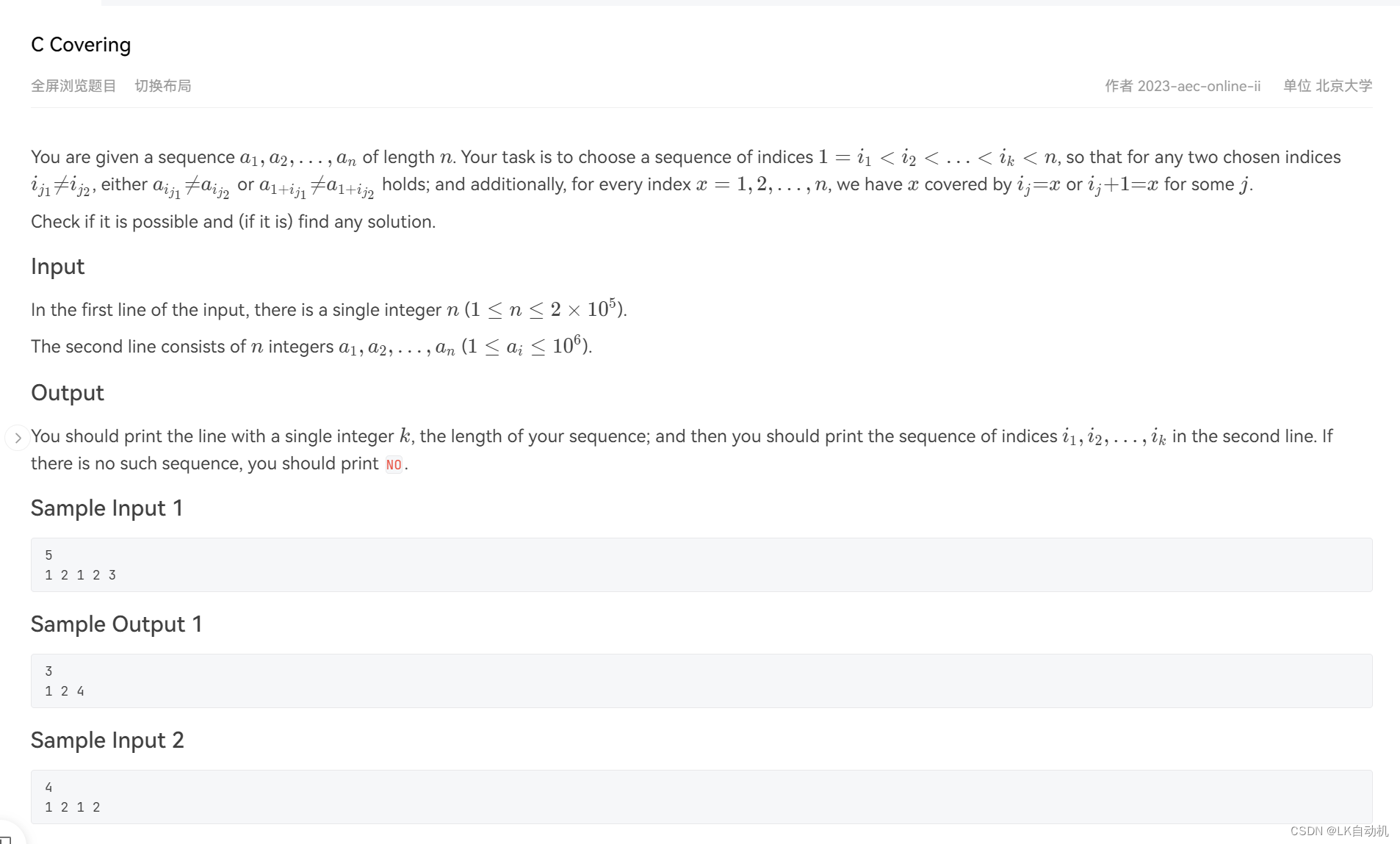
对于限制1，其实就是把 $i$ 分成了若干个集合，每个集合只能选1个点。但如果用2-SAT做就会有 $O(n^2)$ 条边，所以需要考虑前缀和优化建图。

首先看看暴力建的图长啥样：

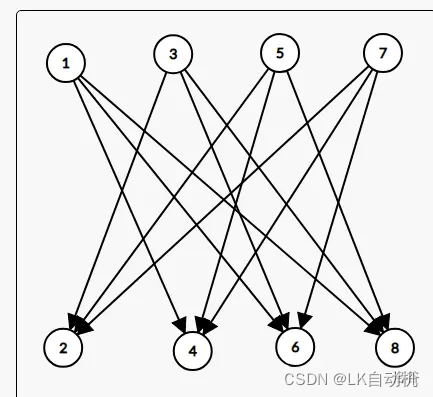
现在我们额外开2*n个点，分别用于前缀和后缀

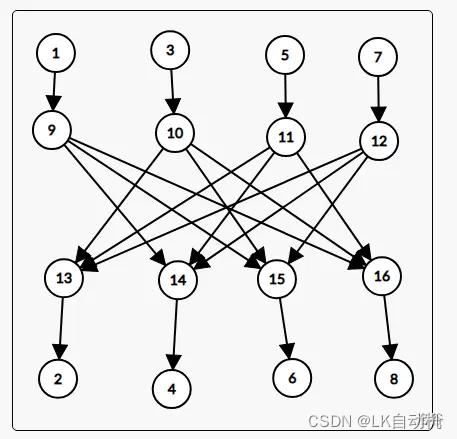
显然 $9\to 15$ 等价于 $9\to 10\to 15$，而类似的，我们会发现只要将第二层和第三层每一层的每个节点之间都互相连边就可以了，然后再稍稍优化下得到：

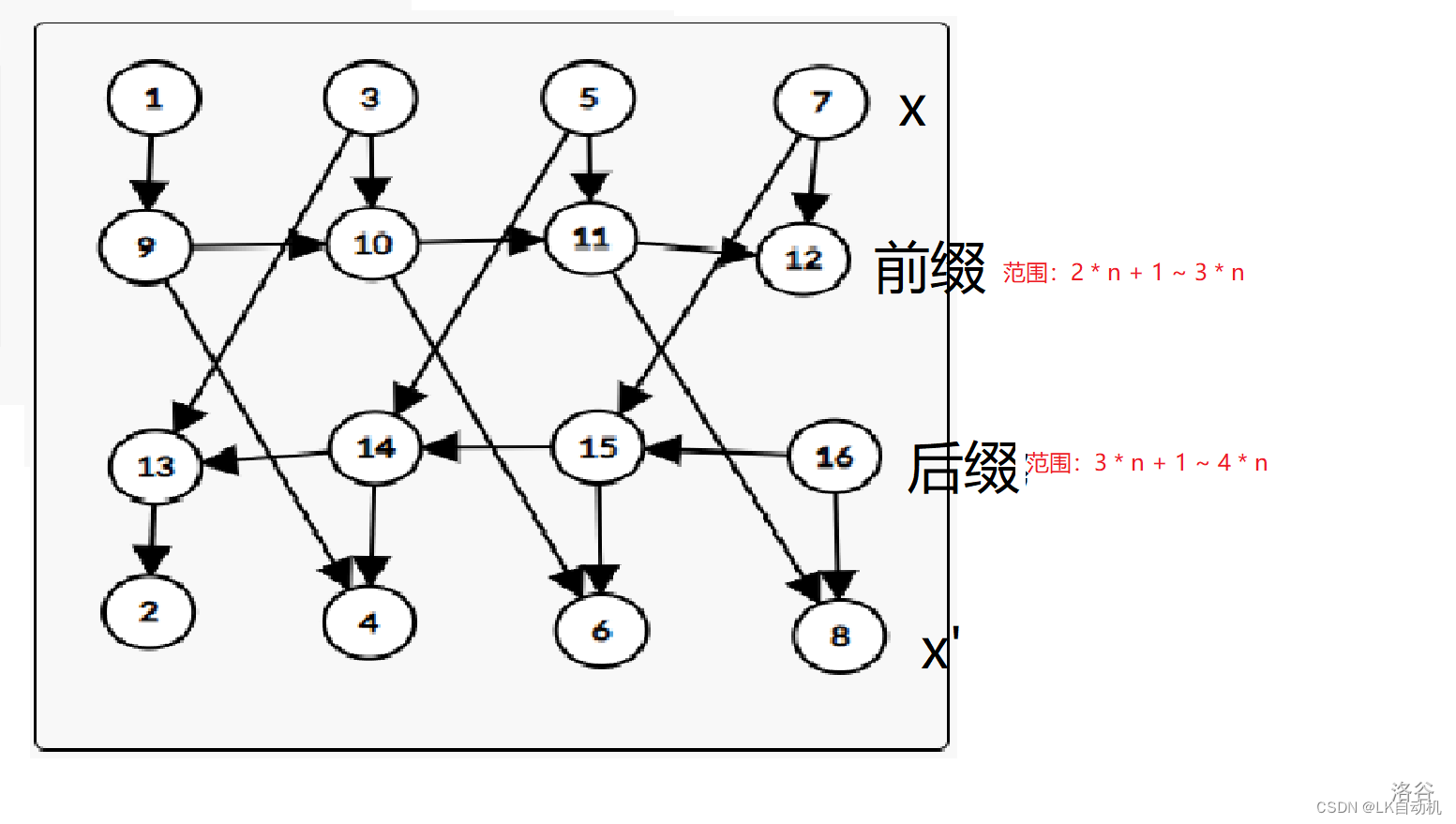
可以发现，我们这个图和原图是等价的。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e6+77;
int dfn[N],low[N],b[N],s[N],c[N],ls[N],cnt,id,top,tot,a[N],tt;
vector<int> p[N],ans;
map<int,int> mp;
struct E
{
	int to,next;
}e[N<<1];
void add(int u,int v)
{
	e[++cnt].to=v; e[cnt].next=ls[u]; ls[u]=cnt;
}
void tarjan(int u)
{
	dfn[u]=low[u]=++tot; b[u]=1;
	s[++top]=u; 
	for(int i=ls[u]; i; i=e[i].next)
	{
		int v=e[i].to;
		if(!dfn[v]) tarjan(v),low[u]=min(low[u],low[v]);
		else if(b[v]) low[u]=min(low[u],dfn[v]);
	}
	if(low[u]==dfn[u])
	{
		id++;
		while(s[top+1]!=u)
		{
			c[s[top]]=id;
			b[s[top]]=0; top--;
		}
	}
}
void solve()
{
	int n;
	cin>>n;
	for(int i=1; i<=n; i++)
	{
		cin>>a[i];
	}
	
	for(int i=1; i<n; i++)
	{
		int v=a[i]*n+a[i+1],t=0;
		if(!mp[v])
		{
			mp[v]=++tt;
			t=tt;
		}
		else t=mp[v];
		p[t].push_back(i);
	}
	
	for(int i=2; i<=n; i++)
	{
		add(i+n,i-1);
		if(i!=n) add(i+n,i+1);
	}
	
	for(int i=1; i<=n; i++)
	{
		add(i,i+2*n);
		add(i+3*n,i+n);
	}
	
	add(n+1,1); add(n,n+n);//1±ØÐëÑ¡ n²»ÄÜÑ¡
	
	for(int i=1; i<=tt; i++)
	{
		for(int j=0; j<p[i].size()-1; j++)
		{
			add(p[i][j]+2*n,p[i][j+1]+2*n);
			add(p[i][j+1]+3*n,p[i][j]+3*n);
		}
		for(int j=0; j<p[i].size(); j++)
		{
			if(j<p[i].size()-1)
			{
				add(p[i][j]+2*n,p[i][j+1]+n);
			}
			if(j)
			{
				add(p[i][j],p[i][j-1]+3*n);
			}
		}
	}
	
	for(int i=1; i<=4*n; i++) if(!dfn[i]) tarjan(i);
	
	for(int i=1; i<=n; i++)
	{
		if(c[i]==c[i+n])
		{
			cout<<"NO"; return;
		}
	}
	for(int i=1; i<=n; i++)
	{
		if(c[i]<c[i+n]) ans.push_back(i);
	}
	cout<<ans.size()<<"\n";
	for(int i=0; i<ans.size(); i++) cout<<ans[i]<<" ";
}
signed main()
{
	ios::sync_with_stdio(false); cin.tie(0),cout.tie(0);
	
	int T=1;
//	cin>>T;
	while(T--)
	{
		solve();
	}
}