package KeepCoding.algorithm;
//位运算知识点
/* 1.   0 ^ x = x  x ^ x = 1
*  2.   位运算满足结合律和交换律，即运算顺序无关
*/
//位运算练习题
//1.整数数组中有一个出现次数为奇数的整数，其余整数的出现次数均为偶数个，请找出数组中这位出现次数为奇数的整数并输出。
//2.整数数组中有两个出现次数为奇数的整数，其余整数的出现次数均为偶数个，请找出数组中这位出现次数为奇数的整数并输出。
public class Demo01 {
    public static void main(String[] args) {
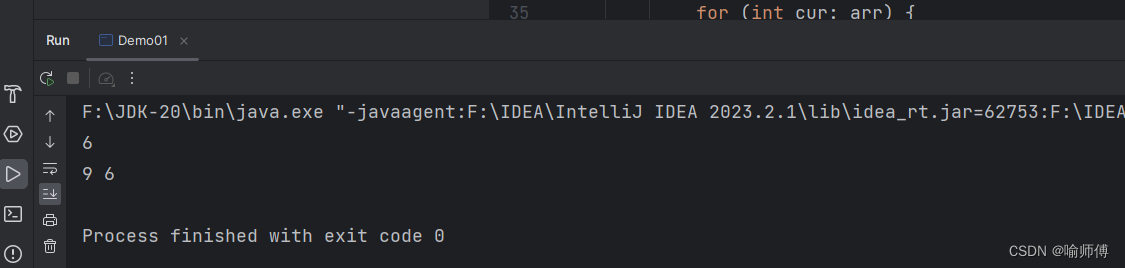
        int [] arr1 = {2,2,3,3,4,4,99,99,6};
        int [] arr2 = {2,2,3,3,4,4,99,99,6,9};
        findOdd(arr1);
        findTwoOdd(arr2);
    }
    public static void findOdd(int[] arr){
        int eor = 0;//定义eor存放所求整数
        for (int cur: arr) {
            eor^=cur;//0^x=x   x^x = 0 所以 eor与数组所有元素进行异或之后即可得出 出现奇数次的那一个
        }
        System.out.println(eor);
    }
    public static void findTwoOdd(int[] arr){
        int eor = 0;//存放
        for (int cur: arr) {
            eor^=cur;//因为偶数个异或都是0，所以最后eor=a^b
        }
        //因为题中说明了 a ！= b 所以 eor不等于0  即eor的二进制上必然有一个位置上是一
        //不妨设第n位为1，并且将数组分为两组，A组n位为1，B组n位为0
        //因为a不等于b，所以a，b不可能在一组，设a在A组，则用eor异或A组中所有的元素即可得到a（偶数个数异或都为0了）
        //eg. A组 a a a 2 2 6 6 ；用eor=a^b ^ 2 2 6 6 a a a  结果是a

        int rightOne = eor & (~eor+1);//这一步即可获得0000 0100这种只有一个1的数，提取出最右的1，用来分组
        int eor$ = 0;//存放
        for (int cur: arr) {
            if ((cur & rightOne)==0){//分组作用

                eor$^=cur;//只跟A组或者B组比较，即可得到a 或者 b

            }
        }
        //eor=a^b  eor$ =a 或者 b  则 eor^eor& = a 或 b
        System.out.println((eor$^eor)+" "+eor$);

    }

}