- 标题:Pointer Networks
- 文章链接:Pointer Networks
- 参考代码(非官方):keon/pointer-networks
- 发表:NIPS 2015
- 领域:序列模型(RNN seq2seq)改进 / 深度学习解决组合优化问题
- 【本文为速览笔记,仅记录核心思想,具体细节请看原文】
- 摘要:我们引入了一种新的神经网络结构,用于学习一个输出序列的条件概率,其中输出序列的元素是对应于输入序列位置的离散标记。这类问题不能通过Seq2Seq模型和神经图灵机等现有方法轻松解决,因为(这些问题中)输出每一步的目标类别数量取决于输入的长度,而输入的长度是可变的。排序可变长度序列、各种组合优化问题等属于这类问题。我们的模型使用了最近提出的神经注意力机制,来解决可变长度输出字典的问题。与先前的注意力机制不同的是,我们的模型不是在每个解码器步骤中将编码器的隐藏单元与上下文向量混合,而是使用注意力作为指针来选择输入序列的成员作为输出。我们将这种结构称为指针网络(Ptr-Net)。我们在平面凸包(planar convex hulls)、计算德劳内三角剖分(computing Delaunay triangulations)和旅行商问题(TSP)三个有挑战性的几何问题上验证了指针网络有能力以 Data-driven 的形式学到近似解。指针网络不仅改进了具有输入注意力的序列到序列模型,还能够推广到可变长度输出字典。我们展示了训练的模型在超过其训练最大长度的情况下也能泛化
文章目录
- 0. 本文考虑的问题
- 1. 传统方法及其问题
- 1.1 Sequence-to-Sequence Model
- 1.2 Content Based Input Attention
- 1.3 问题
- 2. 本文方法
- 3. 实验
- 4. 总结
0. 本文考虑的问题
-
本文主要考虑那些 “输出序列是离散的,并对应于输入序列中位置” 的 Seq2Seq 问题。实验的问题包括
平面凸包问题planar convex hulls:给定平面上若干个点的坐标,输出一组点的索引,使得这些点围成的多边形可以覆盖所有点计算德劳内三角剖分computing Delaunay triangulations:给定平面上若干个点的坐标,以点索引形式输出德劳内三角剖分结果(这是一种以最近的三点形成三角形,且各线段皆不相交的三角网剖分方式)
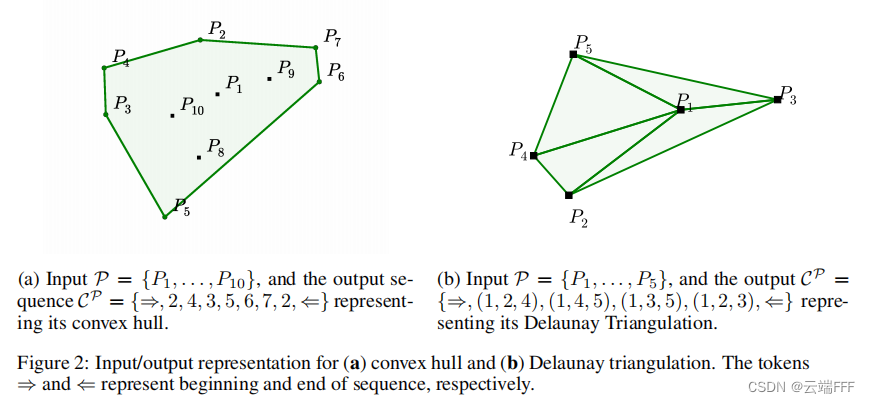
除了以上两个例子外,很多组合优化问题也具有这种形式,作者测试了 Tsp 问题。作者开源了以上三类问题的数据集
-
注意这类问题的特点是:
输出序列的每个元素都是输入序列包含的位置索引,输入序列长度 = 输出索引范围
1. 传统方法及其问题
1.1 Sequence-to-Sequence Model
- 本文是对 Seq2Seq 模型的一个改进,Seq2Seq 模型用于把一个序列转换成另外一个序列,且不要求输入序列和输出序列等长,典型应用有机器翻译等

如上图所示,Seq2Seq 模型通常使用 RNN 及其变种(LSTM/GRU)以 encoder-decoder 结构构建。RNN 类模型内部有一个隐状态代表目前积累的信息,每读入一个序列样本就将其更新,隐变量值可以较好地捕获前驱序列特征。通常使用两个独立的 RNN 模型,一个作为 encoder 提取输入序列的特征,另一个作为 decoder 以 Autoregress 形式解码得到输出序列 - 考虑第 0 节的问题,形式化地讲,给定训练样例
(
P
,
C
P
)
(\mathcal{P}, \mathcal{C^P})
(P,CP),Seq2Seq 模型使用参数模型计算条件概率
p ( C P ∣ P ; θ ) = p ( C 2 ∣ C 1 , P ; θ ) ⋅ p ( C 3 ∣ C 2 , C 1 , P ; θ ) ⋅ ⋅ ⋅ p ( C m ( P ) ∣ C m ( P ) − 1 , C m ( P ) − 2 , . . . , C 0 , P ; θ ) = ∏ i = 1 m ( P ) p ( C i ∣ C 1 , … , C i − 1 , P ; θ ) \begin{aligned} p(\mathcal{C}^{\mathcal{P}}|\mathcal{P};\theta) &= p (C_2|C_1,\mathcal{P};\theta)·p (C_3|C_2,C_1,\mathcal{P};\theta) ···p (C_{m(\mathcal{P})}|C_{m(\mathcal{P})-1},C_{m(\mathcal{P})-2},...,C_0,\mathcal{P};\theta) \\ &=\prod_{i=1}^{m(\mathcal{P})}p (C_{i}|C_{1},\ldots,C_{i-1},\mathcal{P};\theta) \end{aligned} p(CP∣P;θ)=p(C2∣C1,P;θ)⋅p(C3∣C2,C1,P;θ)⋅⋅⋅p(Cm(P)∣Cm(P)−1,Cm(P)−2,...,C0,P;θ)=i=1∏m(P)p(Ci∣C1,…,Ci−1,P;θ) 其中 P = { P 1 , … , P n } \mathcal{P}=\{P_{1},\ldots,P_{n}\} P={P1,…,Pn} 是包含 n n n 个向量的输入序列(上图中的 v v v), C P = { C 1 , … , C m ( P ) } \mathcal{C}^{\mathcal{P}}=\{C_{1},\ldots,C_{m(\mathcal{P})}\} CP={C1,…,Cm(P)} 是由 m ( P ) m(\mathcal{P}) m(P) 个索引组成的序列,每个索引取值范围为 [ 1 , n ] [1,n] [1,n]。直观地看这个条件概率就是模型解码出目标序列的概率。注意目标序列的长度 m ( P ) m(\mathcal{P}) m(P) 通常取决于 P \mathcal{P} P。学习目标是最大化训练集中所有样本的上述概率之和,即
θ ∗ = arg max θ ∑ P , C P log p ( C P ∣ P ; θ ) , \theta^{*}=\operatorname*{arg\,max}_{\theta}\sum_{\mathcal{P},\mathcal{C}^{ \mathcal{P}}}\log p(\mathcal{C}^{\mathcal{P}}|\mathcal{P};\theta), θ∗=θargmaxP,CP∑logp(CP∣P;θ), 训练之后评估阶段,给定输入序列 P \mathcal{P} P,使用学习到的参数 θ ∗ \theta^{*} θ∗ 选择具有最高概率的序列
C ^ P = arg max C P p ( C P ∣ P ; θ ∗ ) \hat{\mathcal{C}}^{\mathcal{P}}=\operatorname*{arg\,max}_{\mathcal{C}^{\mathcal{P}}}p(\mathcal{C}^{\mathcal{P}}|\mathcal{P};\theta^{*}) C^P=CPargmaxp(CP∣P;θ∗) 由于输出序列空间大小为 n m ( P ) n^{m(\mathcal{P})} nm(P),找到真正的最大概率输出序列的计算量太大,工程上通常使用贪心或者 beam search 方法进行解码
1.2 Content Based Input Attention
-
RNN 类模型只能利用隐状态间接地获取之前序列的信息,由于隐藏状态维度一定远远小于之前的变长序列所有样本的连接维度,这种做法无可避免地会损失一些信息。一种补偿方式是引入额外的 Attention 模块,它对整个输入序列的所有 hidden state e 1 , . . . , e n e_1,...,e_n e1,...,en 构造 key 向量,之后在任意第 i i i 个解码位置,用其 hidden state d i d_i di 构造 query 并和整个输入序列计算 attention,根据 attention 结果汇聚(加权平均)整个输入序列的 hidden state,最后用得到的结果和 d i d_i di 做 concatenate 来增强解码时信息输入,缓解信息损耗问题。下图是一个示意

-
形式化地,设 encoder 和 decoder 的隐藏状态为 ( e 1 , … , e n ) (e_{1},\ldots,e_{n}) (e1,…,en) 和 ( d 1 , … , d m ( P ) ) (d_{1},\ldots,d_{m(\mathcal{P})}) (d1,…,dm(P)),如下计算每个输出时刻 i i i 的附加信息
u j i = v T tanh ( W 1 e j + W 2 d i ) j ∈ ( 1 , … , n ) a j i = softmax ( u j i ) j ∈ ( 1 , … , n ) d i ′ = ∑ j = 1 n a j i e j \begin{aligned} u_{j}^{i} & =v^{T} \tanh \left(W_{1} e_{j}+W_{2} d_{i}\right) & j \in(1, \ldots, n) \\ a_{j}^{i} & =\operatorname{softmax}\left(u_{j}^{i}\right) & j \in(1, \ldots, n) \\ d_{i}^{\prime} & =\sum_{j=1}^{n} a_{j}^{i} e_{j} & \end{aligned} ujiajidi′=vTtanh(W1ej+W2di)=softmax(uji)=j=1∑najiejj∈(1,…,n)j∈(1,…,n) 注意这里使用了比较早期的加性注意力,向量 v v v 和矩阵 W 1 , W 2 W_1,W_2 W1,W2 是三组要学习的参数。最后用增强后的 [ d i , d i ′ ] [d_i, d_i'] [di,di′] 作为隐状态进行解码。这种方式相对 1.1 节的朴素 Seq2Seq 方法有显著性能提高
1.3 问题
- 以上两个方法虽然也能部分解决第 0 节的问题,但它们都有一个显著缺陷,即处理问题的尺度无法随着输入泛化:对于每个不同的输入长度 n n n 都要单独训练一个模型。这个问题的本质在于模型无法动态地从输入序列中构造词表,训练时都是事先根据问题规模设置好词表大小的
2. 本文方法
- 作者解决 1.3 节问题的思路很直接,他注意随着输入序列长度的变化,attention 范围可以自适应地变化,所以解码过程中只要想办法自回归地让 attention 像指针一样指出输入序列中的目标位置即可。这其实是对 1.2 节 decoder 的一种简化,我们不再需要根据 attention 汇聚特征再做分类任务,而是直接用经过 softmax 的 attention 向量做分类,这样输出空间可以根据输入序列长度自动调整。示意图如下

图(a) 是 1.1 节的朴素 Seq2Seq 模型,图(b) 是作者提出的指针网络模型 - 形式化地,如下用 attention 机制改写 1.1 节中对
p
(
C
i
∣
C
1
,
…
,
C
i
−
1
,
P
)
p(C_{i}|C_{1},\ldots,C_{i-1},\mathcal{P})
p(Ci∣C1,…,Ci−1,P) 建模的方式
u j i = v T tanh ( W 1 e j + W 2 d i ) j ∈ ( 1 , … , n ) p ( C i ∣ C 1 , … , C i − 1 , P ) = softmax ( u i ) \begin{aligned} u_{j}^{i} & =v^{T} \tanh \left(W_{1} e_{j}+W_{2} d_{i}\right) \quad j \in(1, \ldots, n) \\ p\left(C_{i} \mid C_{1}, \ldots, C_{i-1}, \mathcal{P}\right) & =\operatorname{softmax}\left(u^{i}\right) \end{aligned} ujip(Ci∣C1,…,Ci−1,P)=vTtanh(W1ej+W2di)j∈(1,…,n)=softmax(ui) 这里 u j i u_j^i uji 是长度为 n n n 的注意力得分向量, softmax \operatorname{softmax} softmax 操作将其转换为输入序列上的分布,直接把这个 attention 分布看作在尺寸为 n n n 的词表上做分类时的 softmax 分布,使用交叉熵损失进行优化即可
3. 实验
- 这里仅介绍 TSP 上的结果,另外两个问题详见论文
TSP 问题是说给定一个城市列表,希望找到一个最短的路线,要求把每个城市访问一次并能返回到起点。作者假设两个城市之间的距离是对称的,即 A->B 的距离 = B-> A 的距离。
- 数据生成: 任意训练样本 ( P , C P ) (\mathcal{P}, \mathcal{C^P}) (P,CP) 中, P = { P 1 , … , P n } \mathcal{P}=\{P_{1},\ldots,P_{n}\} P={P1,…,Pn} 是在 [0,1]×[0,1] 区间中随机采样的 n n n 个笛卡尔坐标, C P = { C 1 , . . . , C n } \mathcal{C^P} = \{C_1,...,C_n\} CP={C1,...,Cn} 是一个从 1 到 n 的排列,代表最优路线。为了一致性,在训练数据集中,数据集总是从第一个城市开始。为了生成精确的数据,城市数量不一样,所构建的数据集输出结果方式也不一样,具体地说: 在城市数量 n ≤ 20 n\leq 20 n≤20 的情况下,采用 Held-Karp 算法;对于 n > 20 n>20 n>20 的情况,作者考虑了 A1 A2 A3 三种启发式搜索算法,其中 A3 算法保证在离最优长度1.5倍的范围内找到一个解
- 模型设置:所有模型都使用了具有 256 或 512 个隐藏单元的单层 LSTM;使用随机梯度下降(SGD)训练;学习率为1.0;batch_size为128;随机均匀权重初始化从 -0.08 到 0.08;L2正则化梯度裁剪为 2.0
- 实验结果如下

- 由于 TSP 问题是有约束的(不能重复访问城市,也不能忽略城市),作者在解码时的波束搜索(beam Search)过程中过滤有效的结果。这种过滤过程在 n > 20 n>20 n>20 时是必须的。当 n = 30 n=30 n=30 时(超过训练时城市数量),失败率到达 30%;当 n = 40 n=40 n=40 时失败率上升到 98%
- 表中 OPTIMAL 列是真实最优结果,缺少 n = 50 n=50 n=50 的结果是因为计算复杂度太高了
- 表中第一组行显示了在 n n n 相同时使用最优数据训练的结果。注意到使用最差的算法 (A1) 数据来训练 Ptr-Net 时,模型优于其试图模仿的A1算法(6.42 < 6.46)
- 表中第二组行显示了在5~20个城市的最佳数据上训练的 Ptr-Nets 如何能够推广到更多的城市。 结果对于n=25来说几乎是完美的,对于n=30来说是好的,但在40或更长的时间里似乎会崩溃(尽管如此,结果还是比随机策略要好得多)
4. 总结
- Pointer Networks 天生具备从输入序列中提取元素的能力,因此它非常适合用来实现 “复制” 这个功能。NLP 领域很多研究者也确实把它用于复制源文本中的一些词汇。比如摘要任务,由于所需的词汇较多,非常适合使用复制的方法来复制一些词,目前Pointer Networks 已经称为了文本摘要方法中的利器。
- 此外,在组合优化领域,Ptr-Nets 也得到了广泛的应用,并已成为组合优化问题的端到端方法的入门模型,后来基于此模型,研究者也进行了很多改进,比如与强化学习结合,将 Attention 换成 Transformer 中采用的Self- Attention等。总之,Ptr-Nets为组合优化的端到端解决办法起了一个好头,并促使广大研究者进行更加深入的研究