区间合并简介

区间合并模型是一种竞赛里比较常见的模型，他的含义是，给你n个区间，要你合并所有有交集的区间，并求出合并后剩下的区间个数，如区间[1, 4]和[2, 3]可以合并成[1, 4]，但是[1, 2] 和 [3, 4] 不可以合并。
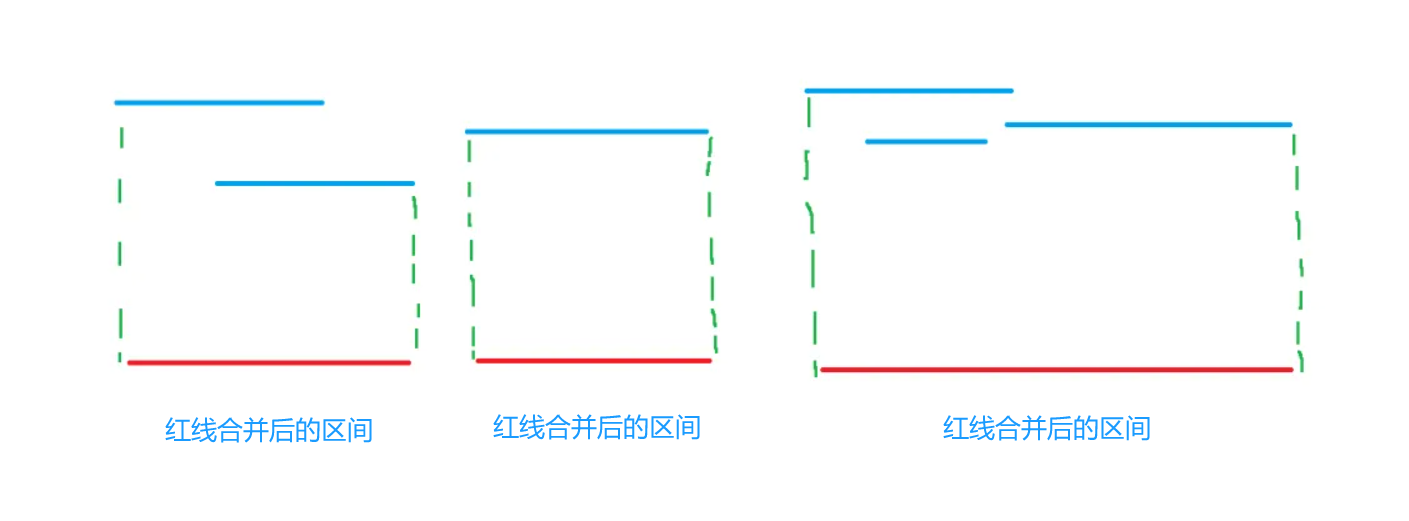
如下图所示，蓝色线段为待合并的区间，红色线段为区间合并后的区间

区间合并算法流程

1. 首先按区间左端点从小到大排序。
   按左端点从小到大枚举所有区间。我们设当前枚举的区间为li, ri当前目标区间(就是判断枚举区间是否可以和该区间合并)为L, R则有区间之间有三种关系,第一种，当前枚举区间包含在目标区间中，如下图，这种情况下目标区间可以不用改变

第二种情况，当前枚举区间与目标区间相交，如下图，这种情况下需要把目标区间的右端点更新成当前枚举区间的右端点。

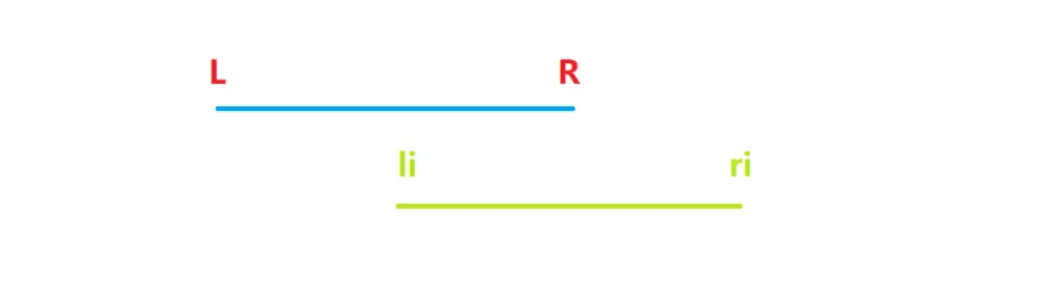
注意，因为区间已经按照左端点排好序了，且是从小到大枚举的，所以下图情况不可能出现

第三种情况，当前枚举区间与目标区间没有相交，如下图，这种情况下就需要把目标区间更新成li, ri

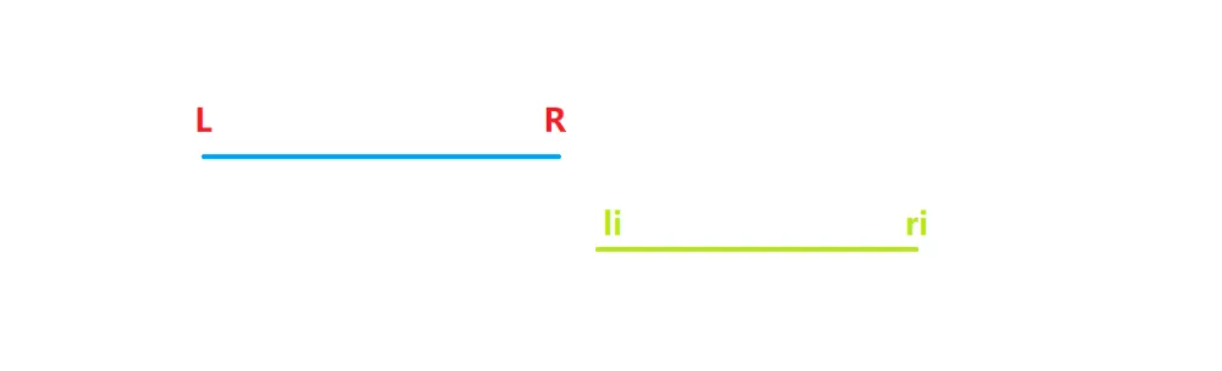
对于上述情况一和情况二，我们可以归结成一种情况，就是判断当前区间和目标区间的右端点谁大，将目标区间右端点更新成较大的那个即可。

时间复杂度

因为区间合并过程中，枚举区间是线性的，因此，按照左端点排序是这个算法的复杂度瓶颈，即O(nlogn)

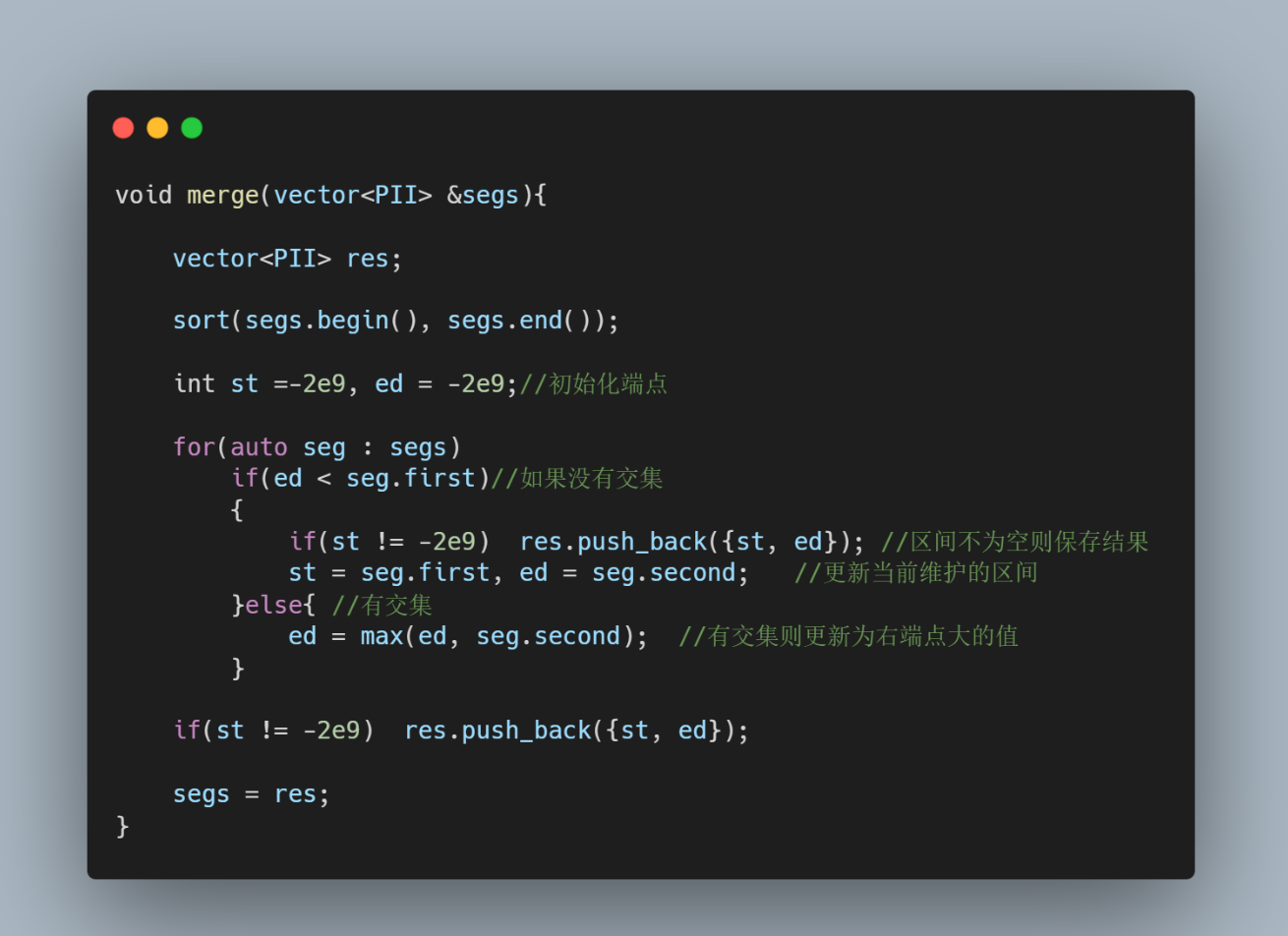
#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

typedef pair<int, int> PII;

const int N = 100010;

int n;
vector<PII> segs;

void merge(vector<PII> &segs)
{
    vector<PII> res;
    sort(segs.begin(), segs.end());
    
    int st = -2e9, ed = -2e9;
    for(auto seg : segs)
        if(ed < seg.first)
        {
            if(st != -2e9) res.push_back({st, ed});
            st = seg.first, ed = seg.second;
        }
    	else ed = max(ed, seg.second);
    
    if(st != -2e9) res.push_back({st, ed});
    
    segs = res;
}

int main()
{
    cin >> n;
    for(int i = 0; i < n; i ++)
    {
        int l, r;
        cin >> l >> r;
        segs.push_back({l, r});
    }
    
    merge(segs);
    
    cout << segs.size();
    
    return 0;
}