【题目链接】
ybt 2074:【21CSPJ普及组】分糖果(candy)
洛谷 P7909 [CSP-J 2021] 分糖果
【题目考点】
1. 数学
取模运算
【解题思路】
只要篮子中有大于等于n颗糖,就要分走n颗糖。最后剩下的归自己的糖的数量一定小于n。这似乎是在做取模运算。
取糖果最少l个,最多r个,这是个连续整数构成的区间。
我们先考察一个连续整数构成的区间的内整数对n取模的结果的规律(即除以n的余数)
| 整数x | 0 | 1 | … | n-1 | n | n+1 | … | 2n-1 | 2n | … |
|---|---|---|---|---|---|---|---|---|---|---|
| x%n | 0 | 1 | … | n-1 | 0 | 1 | … | n-1 | 0 | … |
m是某个正整数
| 整数x | mn | mn+1 | … | mn+n-1 | (m+1)n | (m+1)n+1 | … | (m+1)n+n-1 | (m+2)n | … |
|---|---|---|---|---|---|---|---|---|---|---|
| x%n | 0 | 1 | … | n-1 | 0 | 1 | … | n-1 | 0 | … |
可以看到,x%n的值始终是从0变到n-1,再从0变到n-1。
下图横轴为x,纵轴为x%n,n为6时的示例情况
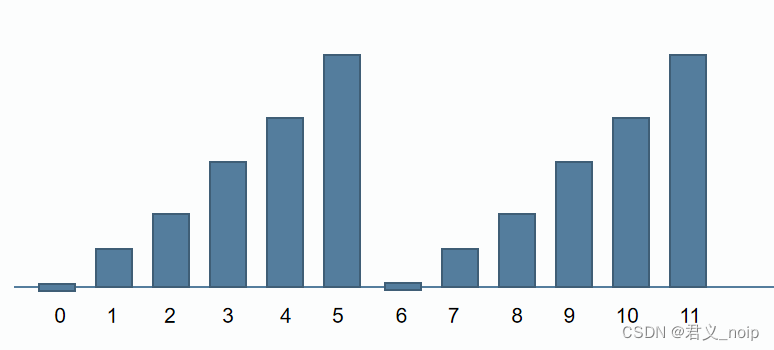
其中,x%n的值每“段”从0变到n-1,都满足x/n的值是不变的。
比如x从 m ⋅ n m\cdot n m⋅n变化到 m ⋅ n + n − 1 m\cdot n+n-1 m⋅n+n−1,x/n的值始终是m,而x%n的值从0变化到n-1
-
如果给定的l与r整除n的值是相同的,即
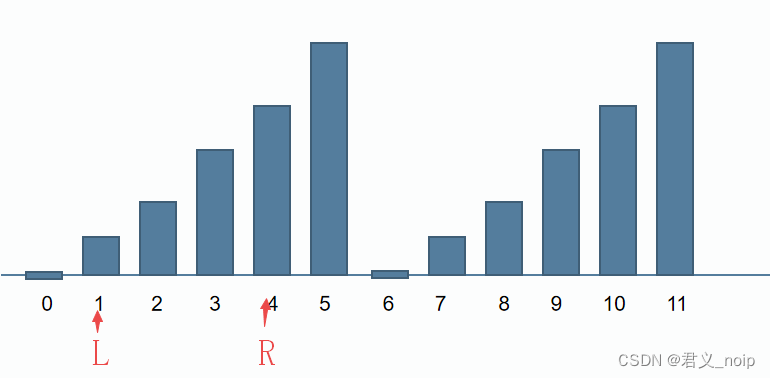
l/n == r/n,那么说明l与r在同一“段”中,x是这一段中的数字。根据上述规律,x从l变化到r的过程中,x%n的值是逐渐增大的,当x为r时,x%n的值最大,为r%n。
下图横轴为x,纵轴为x%n,L,R为满足该描述的一种可能的情况
-
如果给定的l与r整除n的值是不同的,即
l/n != r/n,那么从l到r范围内一定存在一个数字x%n为n-1,一定存在一个数字x%n为0。n-1就是l到r范围内的数字对n取模能得到的最大值。
下图横轴为x,纵轴为x%n,L,R为满足该描述的一种可能的情况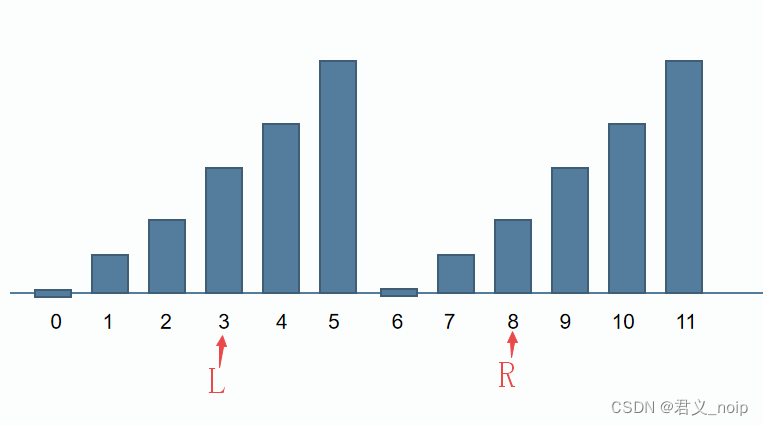
【题解代码】
解法1:
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n, l, r;
cin >> n >> l >> r;
if(l/n == r/n)
cout << r%n;
else
cout << n-1;
return 0;
}